Интегралы в математике

Интеграл – это своего рода обобщение суммы. Он позволяет нам вычислять совокупный эффект от небольших изменений, распределенных по определенному промежутку.

В этой статье мы расскажем все об интегралах: как они работают, каких видов бывают, чем отличаются от дифференциала и разберем несколько примеров использования интегралов в математике.

Интегралы в математике – что это такое

Интегралы занимают особое место в математике, представляя собой один из фундаментальных понятий математического анализа. Они играют ключевую роль в решении множества задач, связанных с нахождением площадей, объемов и других важных характеристик фигур и тел.

История интегралов уходит корнями в глубокую древность. Начало интегрального исчисления можно отнести к работе Архимеда, который использовал метод исчерпывания для нахождения площадей криволинейных фигур. Однако только в XVII веке эта концепция получила четкое математическое определение благодаря трудам Исаака Ньютона и Готфрида Вильгельма Лейбница. Эти математические гении независимо друг от друга разработали основы дифференциального и интегрального исчисления, связав между собой эти два понятия и открыв дорогу для современных исследований.

Как работает интеграл

Интеграл является фундаментальным понятием в математическом анализе и играет важную роль в описании различных физических процессов. Он позволяет нам находить площадь под кривой, вычислять объемы тел, производить вычисления в физике и инженерии, и многое другое. Обычно интеграл используется для определения суммарного эффекта непрерывного процесса или функции на определенном промежутке.

Для нахождения первообразных существуют следующие обозначения:

• ∫ символ интеграла. Он выбран неслучайно: поскольку интеграл представляет собой сумму, которая обозначается как буква S.
• f(x) это функция, которую мы интегрируем.
• dx это указание на то, что каждый интервал является бесконечно малой величиной. Произносится как «дельта икс».

Эти символы впервые ввел в науку в XVII веке немецкий математик Готфрид Вильгельм Лейбниц. Интервал интегрирования обычно указывается в нижней и верхней частях знака интеграла, а сама функция, подлежащая интегрированию, помещается рядом с символом.

Интеграл vs дифференциал

Математический анализ, развивающий тему исчисления с переменными, включает в себя две фундаментальные концепции: интеграл и дифференциал. Оба они являются частью обширного и взаимосвязанного математического мира, их принципы и применения бесценны в различных областях науки и техники.

Интеграл, имеющий свои корни в концепции суммы, стремится к нахождению величин и общей накопленности. Будь то площадь под кривой, объем, или любая иная физическая концепция, требующая интегрирования, этот математический инструмент позволяет математически охватить и формализовать саму суть накопления. Интегралы часто полезны при решении задач, связанных с общими количествами и совокупными эффектами, таких как прогнозирование общей прибыли или измерение расстояний на основе скорости.

Дифференциал предлагает облик мгновенного изменения. Предоставляя инструментарий для вычисления производных, дифференциал неоценим там, где важно понимание инстантных изменений. Дифференциалы широко используют для определения скорости, наклона и ускорения, обеспечивая тем самым основу для аналитического решения уравнений движения и других динамических систем.

Рассмотрим основные различия этих понятий в сравнительной таблице ниже:

Неопределенный интеграл

Неопределенный интеграл представляет собой обратную процедуру дифференцирования и используется для нахождения функций первообразных, исходя из их производных.

В математическом смысле, неопределенный интеграл функции f(x) на языке интегрального исчисления записывается как ∫f(x)dx.

Определение

Неопределенным интегралом функции f(x) называется множество всех ее первообразных. Иными словами, для нахождения неопределенного интеграла необходимо учитывать:

• если F(x) является первообразной функции f(x), то выражение ∫f(x)dx = F(x) + C, где C – произвольная постоянная, представляет собой неопределенный интеграл.

Свойства неопределенного интеграла

Поговорим об основных свойствах неопределенных интегралов:

• Линейность интеграла. Если a и b – константы, а f(x) и g(x) – интегрируемые функции, то: ∫(af(x) + bg(x))dx = a∫f(x)dx + b∫g(x)dx.
• Инвариантность относительно сдвига. Для любой константы c интегралы f(x)dx и f(x + c)dx отличаются только на постоянную величину.
• Производная неопределенного интеграла. Обратная процедура: если F(x) является первообразной f(x), то (d/dx)∫f(x)dx = f(x).
• Интеграл от нуля. ∫0dx = C, где C – произвольная константа.

Определенный интеграл

Определенный интеграл играет важную роль в математическом анализе и находит многочисленные применения в различных отраслях науки и техники. Он представляет собой обобщение понятия суммы для нахождения производных площади под кривой или между кривыми на заданном отрезке. Основная идея заключается в делении области под кривой на бесконечно малые прямоугольники и суммировании их площадей.

Определение

Определенный интеграл от функции f(x) на интервале [a, b] обозначается как ∫[a, b] f(x) dx и представляет собой предел суммы площадей прямоугольников, которые приближают кривую на этом интервале. Эта сумма вытекает из процесса разбивки интервала на бесконечно малые части.

Свойства определенного интеграла

• Линейность. ∫a, b + g(x)) dx = c∫[a, b] f(x) dx + ∫[a, b] g(x) dx для любых чисел c.
• Аддитивность. Если точка c лежит между a и b, то ∫[a, b] f(x) dx = ∫[a, c] f(x) dx + ∫[c, b] f(x) dx.
• Четкость порядка. ∫[a, b] f(x) dx = -∫[b, a] f(x) dx.
• Невыразительность точки. ∫[a, a] f(x) dx = 0.
• Оценочное свойство. Если f(x) непрерывна на [a, b] и f(x) ≥ 0 для всех x ∈ [a, b], то ∫[a, b] f(x) dx ≥ 0.

Полная таблица интегралов

В данном разделе представлена исчерпывающая таблица интегралов, включающая в себя как базовые, так и более сложные выражения, часто встречающиеся в различных областях научных исследований и практики.

Основные формулы таблицы первообразных:

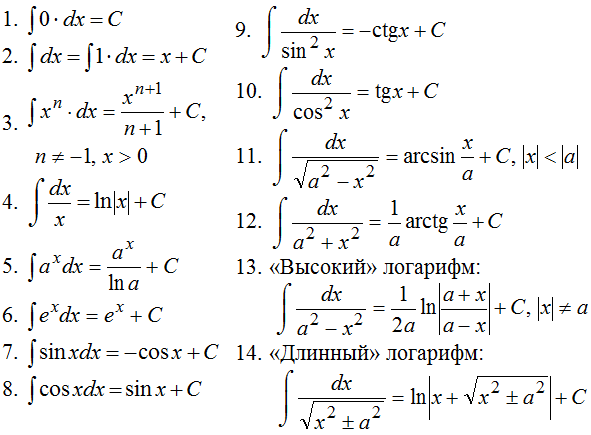
Интегралы от рациональных функций:

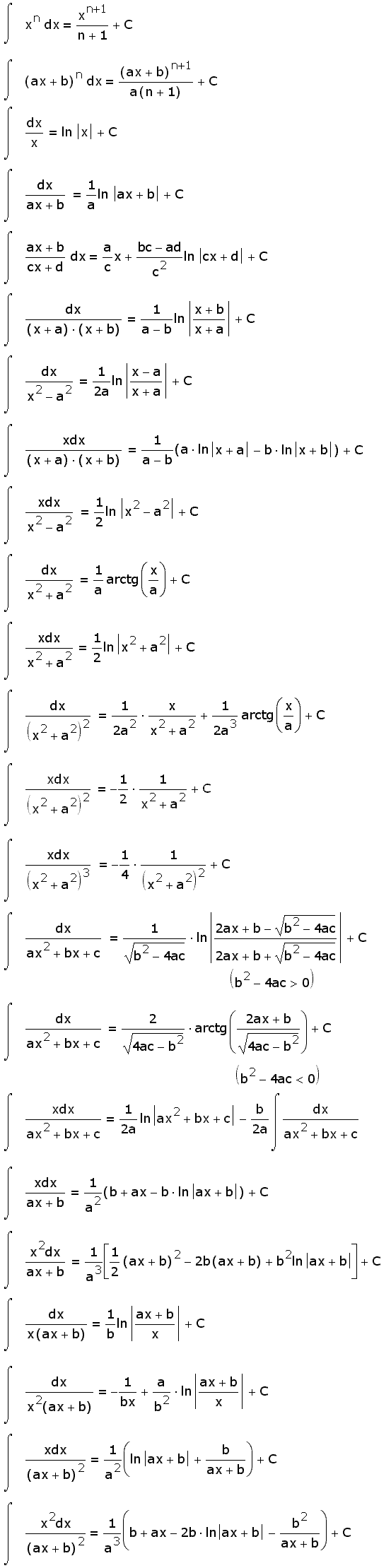
Интегралы от трансцендентных функций:

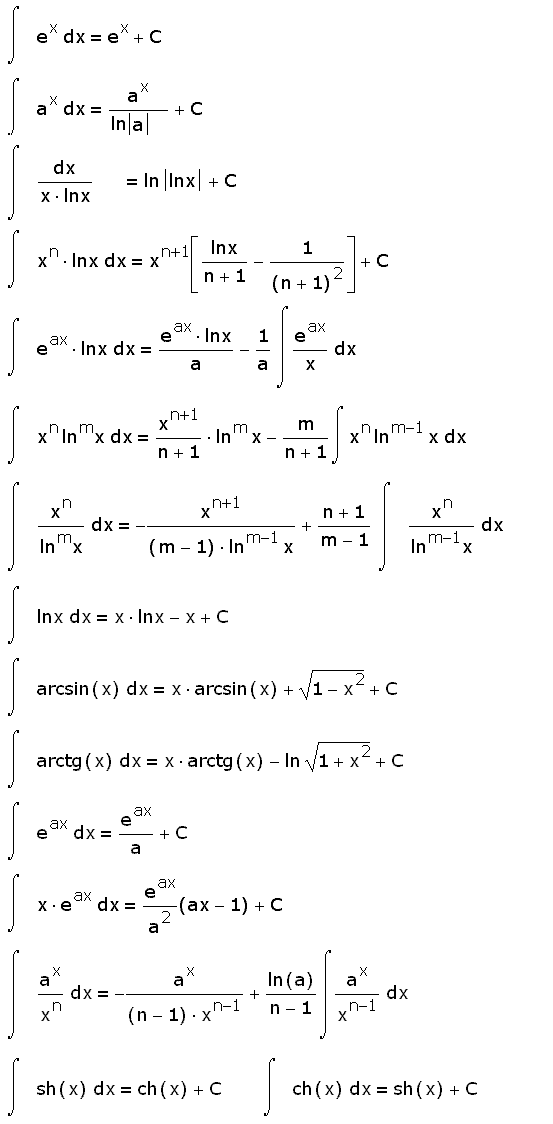
Интегралы от иррациональных функцийтаблицы производных:

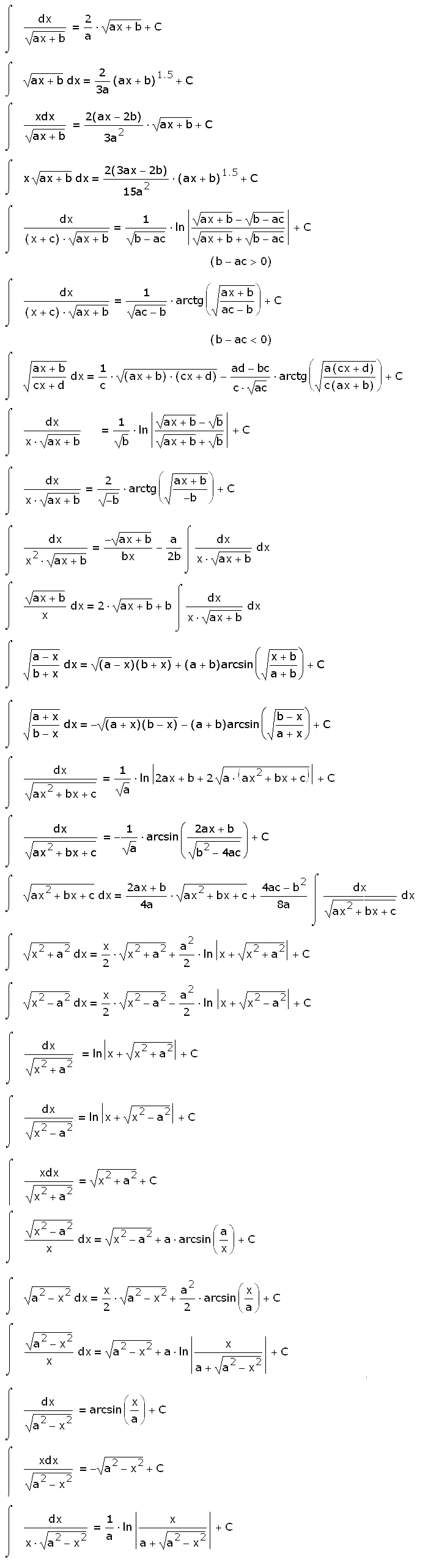
Интегралы от тригонометрических функций:

Как считать интегралы

Давайте разберем, как вычислить интеграл.

Если интеграл представляет сложность, его следует сначала преобразовать, используя различные методы интегрирования. Несмотря на то, что этих методов не так много, они достаточно сложны и многогранны, поэтому мы их не рассматриваем в данной статье.

Важно помнить, что не каждая функция поддается интегрированию. Это возможно только тогда, когда функция определена и непрерывна в области интегрирования.

После того как функция f под интегралом представлена в простейшем виде, необходимо найти ее первообразную. Для этого можно воспользоваться таблицей неопределенных интегралов. Если вы нашли неопределенный интеграл, то результат легко получить, просто подставив значения в формулу. Если же необходимо вычислить определенный интеграл, используйте формулу Ньютона-Лейбница.

Далее нужно провести два преобразования:

1. Сначала определяем первообразную F(x). Константа C в этом случае не добавляется. Этот символ указывает, что мы рассматриваем значения первообразной от a до b.
2. Далее необходимо подставить значения a и b в найденную первообразную, вычислить результат и определить разность этих результатов.

Это и составит определенный интеграл.

Примеры решения

Определенные интегралы служат мощным инструментом в математическом анализе и применяются в различных областях науки и техники. Рассмотрим простые примеры их решения, чтобы лучше понимать этот концепт.

Пример 1

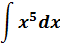
В таблице интегралов такая функция отсутствует.

Однако имеется общий вид интеграла от степенной функции (вторая группа).

В данном случае n равно 5.

Подставляем пятерку вместо n и высчитываем результат:

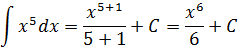
Пример 2

Неопределенный интеграл. Определяем первообразную.

Для этого разделим интеграл суммы на сумму отдельных интегралов.

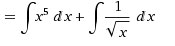
Каждый из интегралов в стандартной форме. Ищем их первообразные в таблице.

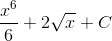
Проверка решения (находим производную):

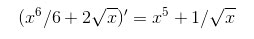
Пример 3

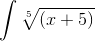
Неопределенный интеграл. Определяем первообразную.

Сравниваем с имеющейся таблицей. В таблице отсутствует.

Не удается разложить, применяя свойства.

Исследуем методы. Оптимально использовать замену переменной.

Заменяем x+5 на t5. Таким образом, t5 = x+5. Тогда получится:

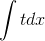
Но dx также следует заменить на t. Если x = t5 - 5, то dx = (t5 - 5)’ = 5t4. Подставляем:

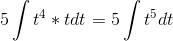
Интеграл из таблицы. Вычисляем:

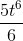
Заменяем t в ответе:

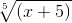
Окончательное решение интеграла:

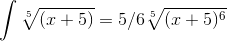
Сложные и особенные случаи

Вычисление интегралов – одна из фундаментальных задач математического анализа. Несмотря на кажущуюся прямолинейность этой области, существуют сложные и особенные случаи, которые требуют пристального внимания и глубокого понимания.

Рассмотрим некоторые из этих случаев:

• Интегралы, при вычислении которых возникают так называемые особые точки или разрывы. Эти точки могут быть как в области определения подынтегральной функции, так и на границе области интегрирования.
• Особые случаи также возникают при работе с несобственными интегралами, когда один или оба предела интегрирования стремятся к бесконечности. Такие интегралы могут быть решены с использованием интегрирования по частям или применения критериев сравнения, чтобы установить условия сходимости. Эти случаи часто требуют рассматривать поведение подынтегральной функции на бесконечности, анализируя ее асимптотические свойства.
• Еще одной сложной и интересной областью являются интегралы, возникающие в комплексном анализе. Для них используется метод вычетов, который позволяет рассчитывать интегралы по замкнутым контурам в комплексной плоскости. Это особенно полезно, когда функция интегрирования имеет полюсы и необходимо аккуратно учитывать вклад каждого из них в общий результат.
• Нельзя обойти вниманием и интегралы, в которых использованы специальные функции, такие как гамма-функция, бета-функция или функции Бесселя. Эти функции появляются во множестве приложений, и их интегралы требуют специальных знаний для вычисления площади. Применение свойств этих функций, а также их представлений в виде рядов и других интегралов, часто позволяет упростить задачу.

Что почитать и посмотреть по теме

Для тех, кто хочет углубиться в тему интегралов, мы собрали лучшие книги и видео, которые помогут лучше понять этот термин.

Книги:

• «Введение в теорию интегралов» В. И. Смирнов.
• «Интегралы для начинающих» Г. И. Маркс.
• «Основы исчисления: интегралы и производные» Джеймс Стюарт.
• «Теория функции комплексной переменной с основами интегралов» Ларс Хормандер.

Видео и лекции:

• «Интегралы в контексте истории» на YouTube канал L. Mathematics.
• Курс лекций «Исчисление: Интегралы» от MIT OpenCourseWare.
• Видео-серия «Интегралы для всех» на Khan Academy.
• «Визуализация интегралов» от 3blue1brown на YouTube.

FAQ

В каком классе начинают учить интегралы?

Интегралы начинают учить в 11 классе общеобразовательной школы или на 2 курсе колледжей и техникумов.

Можно ли самостоятельно научиться вычислять интегралы?

Да. Вы можете самостоятельно научиться вычислять интегралы при помощи книг и видео, которые мы описали выше.

Вывод

• Основная суть интегрирования состоит в процессе суммирования бесконечно малых величин, что позволяет определить функцию на определенном интервале, зная ее поведение на малых участках.
• Интегралы дают возможность нахождения площади под кривыми, объемы тел вращения, длины дуг и многое другое, обеспечивая богатый инструментарий для анализа функционального поведения.
• Вычисление интегралов в сложных и особенных случаях – это не только техническая задача, но и искусство, требующее творческого подхода и глубокого понимания функций и их свойств.
• Решение таких задач расширяет горизонты математического анализа и находит применение в многочисленных областях науки и техники, от теоретической физики до инженерных расчетов.