Бином Ньютона

Биномом Ньютона называют формулу для разложения степени суммы, предложенную Ньютом. Ее применяют при работе с большими числами или переменными.

Понимание и умение использовать бином Ньютона полезно всем, кто увлекается математикой и ее приложениями. Он является примером того, как абстрактные математические концепции находят применение в реальной жизни и помогают решать практические задачи.

Мы расскажем, что такое бином Ньютона простыми словами, где используется формула, приведем примеры расчета и проанализируем возможные ошибки расчетов.

Бином Ньютона

Бином Ньютона или биномиальная теорема — это математическое выражение, которое позволяет находить степень суммы двух чисел или переменных. По определению бином – это двучлен, т. е. сумма двух слагаемых.

Простыми словами, если у нас есть два числа, скажем, a и b, и мы хотим возвести их сумму в какую-то степень n, то бином Ньютона помогает это сделать без необходимости множить (a + b) само на себя n раз.

Кому важно уметь его применять бином Ньютона:

• Школьникам и студентам, которые изучают алгебру и высшую математику, так как он является основой для дальнейшего понимания многих алгебраических концепций.
• Инженерам и физикам, т. к. помогает решать сложные уравнения и модели, где необходимо быстро и точно рассчитывать степени.
• Бизнес-аналитикам и специалистам по данным, которые также могут извлечь из этого пользу. Бином Ньютона позволяет оптимизировать расчеты при анализе больших данных, где каждый процент времени и ресурсов на счету.

Формула бинома Ньютона

Формула бинома Ньютона, представляет собой фундаментальное утверждение алгебры, описывающее разложение степеней суммы двух элементов.

Если:

• a и b — это любые действительные или комплексные числа;
• n — неотрицательное целое число;
• k – номер слагаемого в многочлене;
• С – биноминальные коэффициенты, показывающие, на какие числа нужно умножить каждое слагаемое в многочлене.

Формула бинома Ньютона выглядит следующим образом:

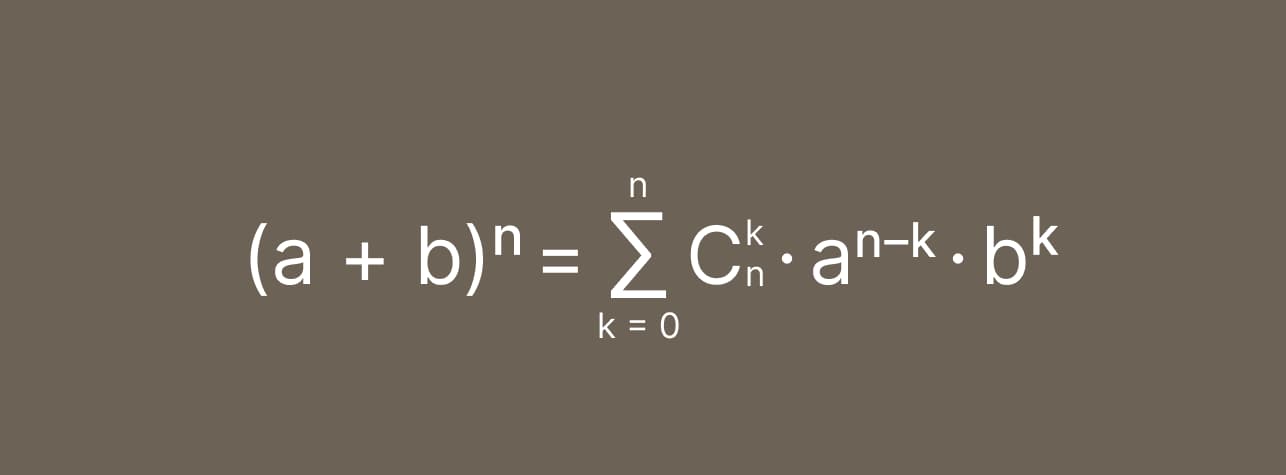
Формула расчета биноминального коэффициента:

Где:

n — степень, в которую возводиться сумма двух чисел;

k — номер слагаемого в многочлене (считается с нуля);

! — факториал. Это произведение всех чисел от 1 до числа, стоящего под знаком факториала. Например, 5! = 1 × 2 × 3 × 4 × 5 = 120.

Как считать

Чтобы произвести расчеты, нужно в формулу подставить заданные числа. Так, если на нужно возвести в квадрат сумму чисел a и b, формула будет выглядеть следующим образом:

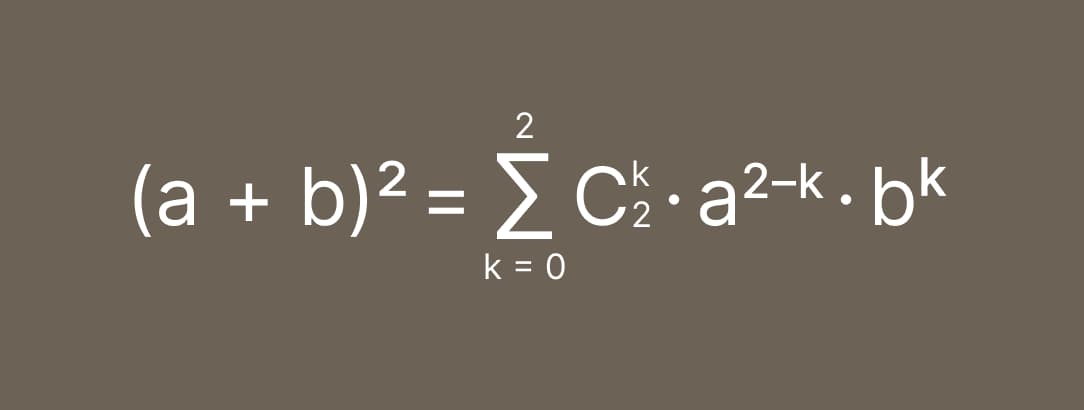
Далее раскрываем знак суммы и выписываем слагаемые:

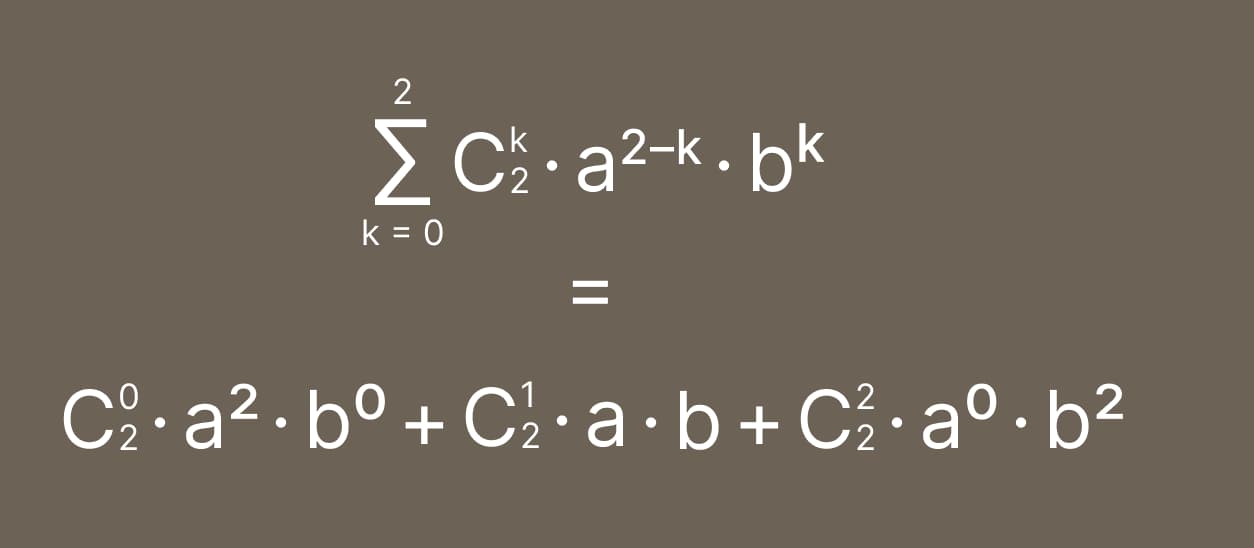
И упростим:

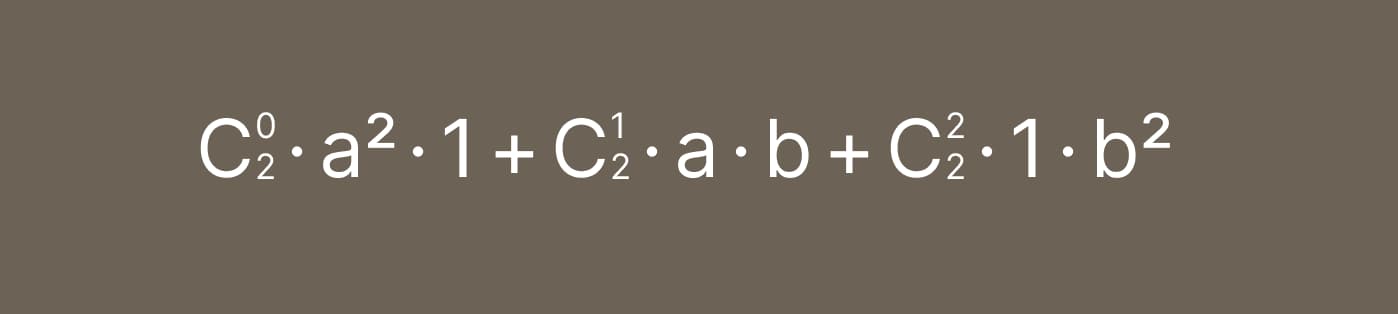
Произведем расчет биноминальных коэффициентов:

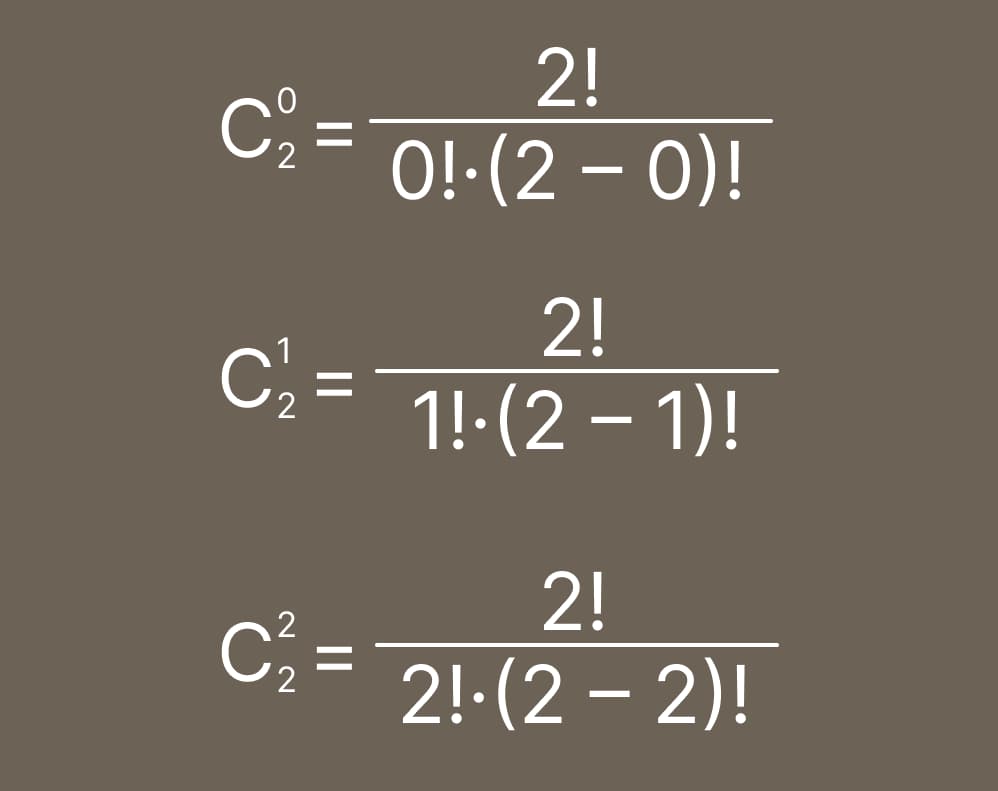
Считаем факториалы и сокращаем:

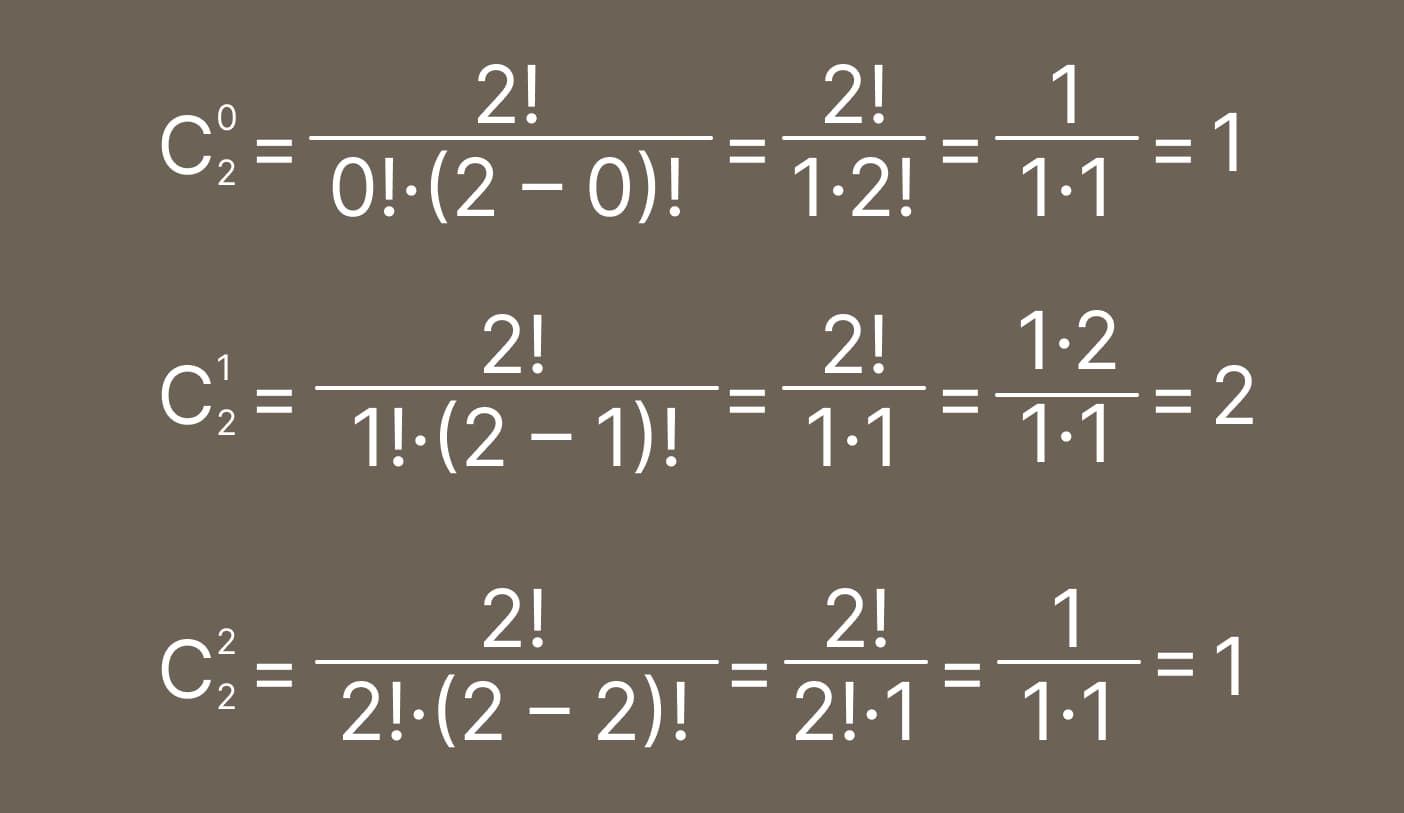
Подставляем полученные коэффициенты в нашу формулу:

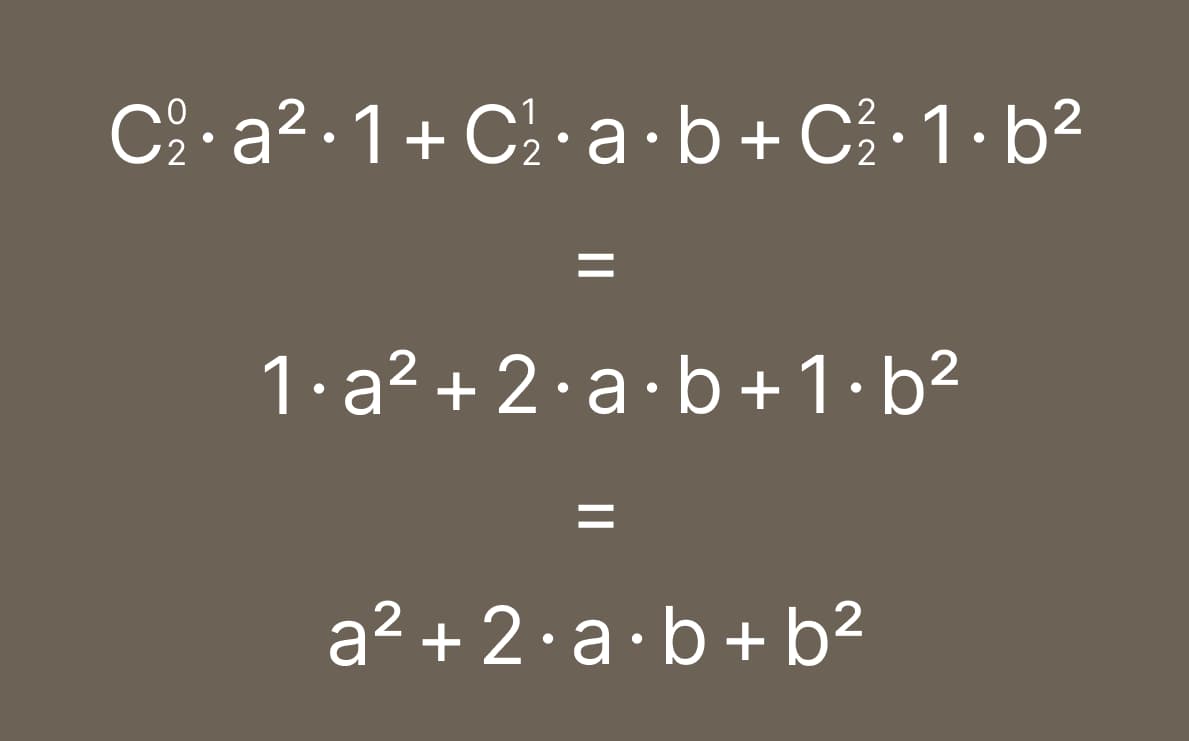
Таким образом, получили, что

(a + b) ² = a ² + 2ab + b ²

Примеры

Степень, в которую возводиться сумма двух чисел, может быть любым неотрицательным целым числом.

Приведем примеры формул разных степеней n:

• (a+b)³=a³+3a²b+3ab²+b³
• (a+b)⁴=a⁴+4a³b+6a²b²+4ab³+b⁴
• (a+b)⁵=a⁵+5a⁴b+10a³b²+10a²b³+5ab⁵+b⁵

Где используется

Формула бинома Ньютона используется, когда нужно найти степень суммы двух чисел.

Однако это не только инструмент для упрощения выражений, но также и формула, которая применяется там, где требуется оценить вероятности и комбинации различных элементов и событий.

Где чаще всего бином Ньютона находит применение:

• В теории вероятностей, где он используется для анализа бинарных случайных процессов. Это особенно полезно в случае поиска вероятностей числовых комбинаций событий. Например, выражение позволяет находить коэффициенты многочленов, возникающих при разложении выражений типа \((1 + x)ⁿ\), что имеет ключевое значение в теории рядов.
• В математике он дал толчок к развитию новых направлений, например теории групп и кольца.
• В комбинаторике он позволяет рассчитать число возможных комбинаций и перестановок объектов.
• В статистике и анализе данных его применяют для оценки вероятностей положительных и отрицательных результатов каких-либо событий.
• В физике и механике он помогает при вычислениях вероятностей исходов экспериментов с частицами и для описания поведения частиц при взаимодействиях.
• В программировании он играет важную роль при создании алгоритмов сжатия данных, криптографии и решения комбинаторных и вероятностных задач.
• В инженерии он используется для оценки вероятности отказа системных компонентов.
• Его применяют в биологии и генетике при анализе встречаемости определенных генотипов или фенотипов в популяциях, а также для моделирования результатов генетических скрещиваний и передачи наследственных признаков.

Как вычислять коэффициенты с помощью треугольника Паскаля

Треугольник Паскаля — это математический инструмент, который помогает вычислять коэффициенты биномиальных разложений. Он назван в честь великого французского математика Блеза Паскаля, хотя подобные конструкции были известны и ранее в различных культурах, включая китайских и персидских математиков.

Основная идея треугольника Паскаля заключается в том, что каждый элемент в треугольнике представляет собой сумму двух элементов, расположенных над ним. Эта конструкция приводит к уникальному и симметричному распределению чисел, которые становятся коэффициентами в биномиальных формулах.

Чтобы построить треугольник Паскаля, начнем с вершины, где находится единица. Следующий уровень треугольника также будет состоять из двух единиц. На третьем уровне мы начнем видеть эффект суммарности: по краям продолжают стоять единицы, а средний элемент равен сумме надлежащих элементов предыдущего уровня — то есть он будет равен 2.

Так и продолжаем, добавляя новые ряды. Каждый элемент \(C(n, k)\), где \(n\) — это номер уровня, а \(k\) — положение элемента в строке (начиная с нуля), можно вычислить по формуле:

\[ C(n, k) = C(n-1, k-1) + C(n-1, k) \]

где \(C(n, 0) = 1\) и \(C(n, n) = 1\).

Эти коэффициенты находятся и в центре известной формулы бинома Ньютона.

Например, чтобы найти коэффициенты для бинома \((x + y)⁴\), мы смотрим на пятый уровень треугольника Паскаля (учитывая, что начинается с нулевого уровня):

\(1, 4, 6, 4, 1\).

Таким образом, разложение будет:

x⁴ + 4x³y + 6x²y² + 4xy³ + y⁴

Этот простой трюк упрощает множество вычислений, особенно при работе с полиномами высокого порядка, экономит время и усилия и дает понимание красоты симметрии в математике.

Ошибки

Ошибки при расчете бинома Ньютона могут возникать по различным причинам, разберем типичные:

• Неправильное определение коэффициентов бинома, что может возникнуть при неверном применении формулы сочетаний. Ошибочное вычисление факториалов или путаница в порядке операции зачастую приводит к неверным результатам.
• Неточности при подстановке значений \(a\), \(b\) и \(n\) в сам полином. Некорректная проверка и обработка этих переменных при каждом шаге раскрытия скобки может привести к общему сбою в порядке и значении итогового выражения.
• Арифметические ошибки также могут повлиять на процесс, особенно при работе с большими числами или в условиях ограниченной вычислительной точности, например, в программировании. Неправильное округление промежуточных значений может привести к значительным отклонениям в результатах.

Для минимизации ошибок необходимо методично подходить к каждому шагу использования бинома Ньютона, проверяя корректность использованных формул, последовательность действий и точность арифметики.

Бином Ньютона в художественной литературе

В художественной литературе бином Ньютона часто фигурирует как синоним чего-то очень сложного и умного, иногда в ироническом контексте.

Вот несколько примеров:

• Повесть Л. Н. Толстого «Юность». Николенька Иртеньев на вступительном экзамене на математический факультет московского университета отвечает на вопрос о биноме Ньютона.
• Роман «Мастер и Маргарита» М. А. Булгакова. Коровьев говорит: «подумаешь, бином Ньютона! Умрет он через девять месяцев, в феврале будущего года, от рака печени в клинике Первого МГУ, в четвёртой палате».
• Повесть «Последнее дело Холмса» А. Конан Дойля. Шерлок Холмс рассказывает о профессоре Мориарти: «…когда ему исполнился 21 год, он написал трактат о биноме Ньютона, завоевавший ему европейскую известность…».

FAQ

Каково происхождение выражения «бином Ньютона» и как этот термин связан с самим Исааком Ньютоном?

Бином Ньютона, известный также как биномиальная теорема, является формулой, которая впервые была систематизирована Исааком Ньютоном. Хотя элементы этого метода были известны ранее, именно Ньютон предложил универсальную формулировку, расширив ее применение на дробные и отрицательные показатели.

Какие практические приложения имеет бином Ньютона в современной науке и технике?

Бином Ньютона используется для упрощения вычислений в различных областях, таких как статистика, вероятностный анализ и даже квантовая физика. Он помогает решать сложные задачи, связанные с комбинаторикой и алгебраической структурой, что делает его фундаментальным инструментом в математическом анализе.

Как бином Ньютона помогает в понимании природы математических рядов и их сходства?

Бином Ньютона позволяет разложить степенные выражения в суммы, что упрощает исследование и анализ бесконечных рядов. Это особенно полезно при разработке алгоритмов и моделей, требующих точных приближений.

Вывод

Бином Ньютона представляет собой один из краеугольных камней современных математических исследований и приложений.

Его универсальность и простота помогает в преодолении математической сложности в разнообразных областях науки, от теоретической физики до инженерного анализа. Понимание и использование бинома Ньютона открывают широкие возможности для решения задач, связанных с числовыми рядами и экспериментальными данными, подтверждая его неоспоримую важность в научной картине мира.