Вычитание дробей

Вычитание дробей кажется очень сложней задачей. Но, если усвоить несколько правил, то решение подобных примеров будет доставлять удовольствие. Расскажем, как минусовать дроби быстро и правильно.

Что такое дробь – понятие

Дробью называют форму записи чисел, которая представляет собой соотношение двух величин. Это могут быть числа или выражения. Существует 2 варианта записи дробей:

• обыкновенная дробь - ⅓;
• десятичная дробь – 0,3.

Величина, расположенная в обыкновенной дроби над чертой, называется числителем и является делимым. Под чертой расположен знаменатель, который является делителем. Соответственно, черта, которая их разделяет, означает знак деления.

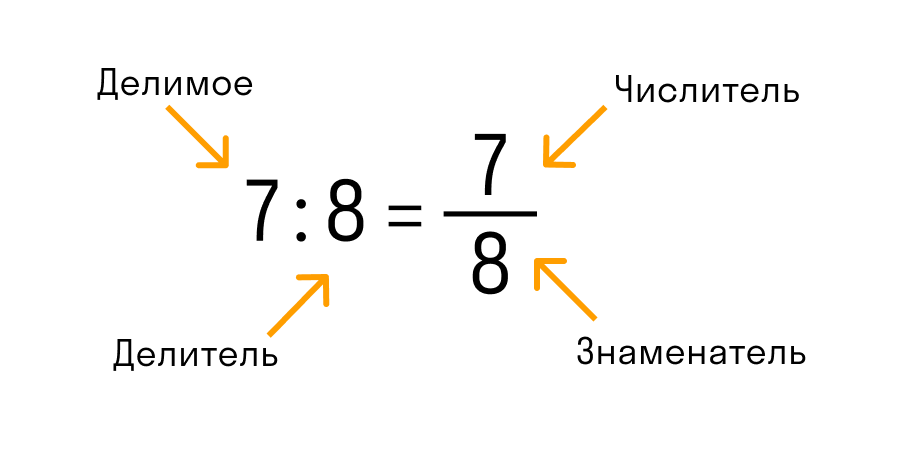
Также дроби бывают:

• числовые (1/2) – дробь, где числитель и знаменатель являются целыми числами;
• алгебраические (а*с/в-с) – дроби, в которых, как числитель так и знаменатель представляют собой переменные величины.

Кроме этого, дроби делят на:

• правильные (3/7) – числитель в такой дроби всегда будет меньше знаменателя;
• неправильные (22/3) – числитель больше или равняется знаменателю.

Вычитание дробей с одинаковыми знаменателями

Это самый простой пример вычитания дробей. Для решения такого примера, знаменатель оставляем такой же, как и в условии, а в числителе от первого числа отнимаем второе.

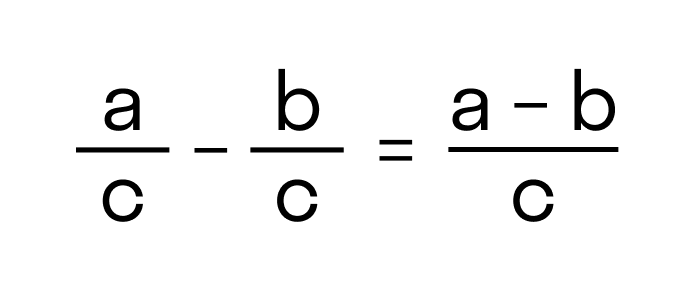
Перед тем, как написать окончательный ответ, важно проверить, нельзя ли полученную дробь сократить.

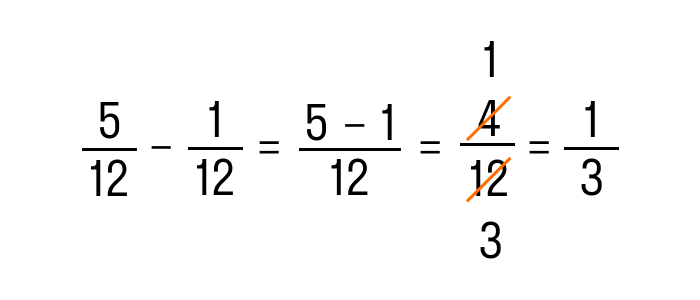
Вычитание дробей с разными знаменателями

При вычитании дробей с разными знаменателями, начинать решение нужно с их приведения к общему знаменателю. После этого останется только найти разность числителей. К примеру, нам необходимо от 2/9 отнять 1/15. Для этого:

• Приводим обе дроби из условия к общему знаменателю. Чтобы его найти, нужно НОК (наименьшее общее кратное).
• НОК находим следующим образом – раскладываем оба знаменателя на простые множители. Делается это следующим образом:
  9=3*3
  15=3*5
• Вначале записываем множитель из первого примера. Для данного примера это: 3*3. После этого добавляет множитель из второго примера, которого не было в первом. В рассматриваемом примере это 5. Перемножив их, мы получим наименьшее общее кратное. Для данного примера НОК (9,15) = 3*3*5=45.
• На следующем этапе рассчитываем дополнительные множители. Чтобы сделать это, полученный НОК делим на каждый из наших знаменателей:
  45/9=5
  45/15=3
• Эти числа нужно умножить на дроби из условия:
  
  
  
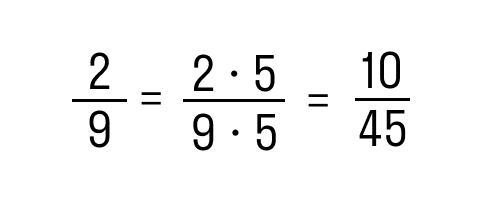
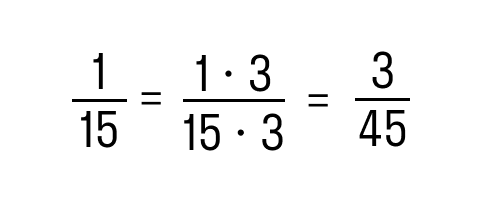
• Последним действием будет непосредственно вычитание наших дробей:
  
  

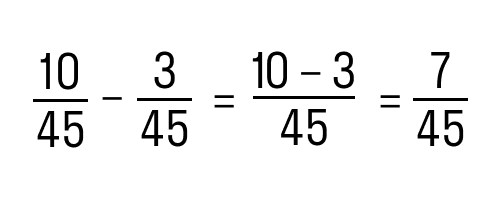
В итоге получаем:

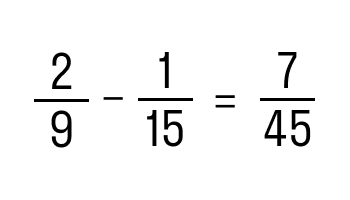
Вычитание дроби из натурального числа

Разберемся, как это делать на примере 3-6/7. Решение будет выглядеть следующим образом:

• Чтобы вычесть из целого числа обыкновенную дробь, для начала целое число нужно представить в виде смешанного числа. Для этого занимаем одну единицу, делая дробь неправильной, то есть такой, у которой знаменатель, такой же, как и знаменатель вычитаемого. 3=2 7/7.
• Осталось отнять дроби.
  
  

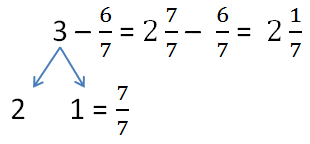
Вычитание натурального числа из обыкновенной дроби

Алгоритм решения такого примера будет аналогичен алгоритму предыдущего примера. То есть целое число представляется в виде неправильной дроби. После чего происходит непосредственно отнимание.

Онлайн калькуляторы – обзор

Чтобы проверить, правильно ли вы научились отнимать дроби, в том числе проводить вычитание смешанных дробей, можно воспользоваться онлайн калькуляторами. В интернете их представлено огромное количество, рассмотрим самые популярные:

1. OnlineMSchool. На сайте можно не только отнимать, но и складывать, делить или умножать дроби, возводить их в степень и выполнять другие действия.
2. Calc.by. Онлайн калькулятор позволяет проводить с дробями любые простые арифметические операции. Для этого достаточно заполнить соответствующие поля.
3. Контрольная работа Ру. Сайт предлагает правильно решить любой пример с дробями и удивить своего учителя математики.
4. Binary2Hex. На сайте можно не только проверить, правильно ли решен пример, но и ознакомиться с подробным его решением.
5. СлонУм. Самый простой калькулятор дробей.

FAQ

Справедливы ли для вычитания дробей, свойства вычитания натуральных чисел?

Да, они справедливы. Это следует из основного смысла, который придают дробям и операцим их вычитания.

Какие ошибки при вычитании дробей допускают чаще всего?

К самым распространенным ошибкам при вычитании дробей относят:

1. Не упрощение ответа. После решения примера, стоит проверить, нельзя ли сократить полученный ответ.
2. Слишком раннее упрощение ответа. Решая пример, необходимо найти общий знаменатель и разницу числителя. И только после этого дробь можно сокращать. Если делать это раньше, до тех пор, пока еще не получен окончательный ответ, возможны ошибки в вычислении или неудобство в решении.

Какие основные свойства есть у дробей?

К основным свойствам дробей относят:

1. Если в знаменателе стоит нуль, то дробь не имеет значения.
2. Если числитель равен нулю, а знаменатель – любое число, которое отличается от нуля, то дробь равняется нулю.
3. Дроби а/b и c/d будут равны, если а* d= b*с.
4. Если числитель и знаменатель в любой дроби умножить или разделить на одинаковое натуральное число, в итоге получится равная дробь.

Как решать сложное уравнение с несколькими вычитаемыми?

Решая сложное уравнение с несколькими вычитаемыми, необходимо действовать последовательно. Только так получится правильный ответ.

Вывод

Главное правило, которое важно запомнить, отнимая дроби – первое, что нужно сделать, решая пример, это привести дроби к общему знаменателю, если они разные по условию. Общим знаменателем является наименьшее общее кратное. Поняв это, решать примеры на отнимание дробей будет просто.