Все формулы приведения
Начнем с того, что название формул привидения происходит от слова «приводить» в значении привести что-то в определенный вид, состояние. В нашем случае формулы приведения помогают упростить сложные тригонометрические функции (аргументы) произвольной величины, то есть не равными синусу, косинусу, тангенсу или котангенсу 0°, 90°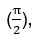 
180° (π), 270° 
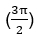и 360° (2π), к функциям углов, лежащих в интервале от 0° до 90° или от 0 до 
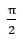радиан. Именно с углами, лежащими в данном диапазоне легче работать, так что формулы приведения активно используются математиками при решении тех или иных задач в тригонометрии.
Формулы приведения – список
Покажем на примере. Вам надлежит вычислить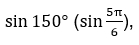 
и, чтобы это сделать, надо воспользоваться одной из формул приведения: 
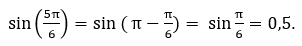Или: sin 150° = sin(180°-30°) = sin(π-30)° = sin 30° = 0,5. Мы привели синус тупого угла к синусу острого угла. Приведем другой пример: tg 765° = tg(360·2+45°) = tg 45° = 1. Здесь мы равным образом привели первоначальный большой угол к острому.
Как можно заметить, мы в примере в качестве уменьшаемого взяли значения, уже очень хорошо известные нам. Как раз использование, так называемых, опорных точек (90° 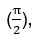180° (π), 270° 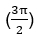и 360° (2π)) помогает нам прийти к упрощенному варианту. Следовательно, формулы приведения имеют общий вид. Это вычитание из значения опорной точки или сложение со значением опорной точки угла α: 
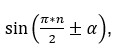, где n – любое число от 1 до 4, а на месте синуса может так же стоять любая другая тригонометрическая функция (косинус, тангенс и котангенс).
Следует отметить, что знак тригонометрической функции может измениться на противоположный в зависимости от четверти, в которой находится угол, полученный в ответе, и самой функции. В приведенном примере угол 30° находятся в первой четверти, а синус в данной четверти со знаком «+», поэтому ответ у нас положителен.
Таким образом, формулы приведения – это тригонометрические тождества, позволяющие привести аргумент функции к значению, удобному для вычисления, и имеющий общий вид в выражении 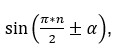, где n – любое число от 1 до 4.
Всего 32 формулы приведения, и их можно разделить на следующие 4 вида в зависимости от опорной точки:
1) Формулы приведения с опорной точкой 90° или :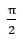
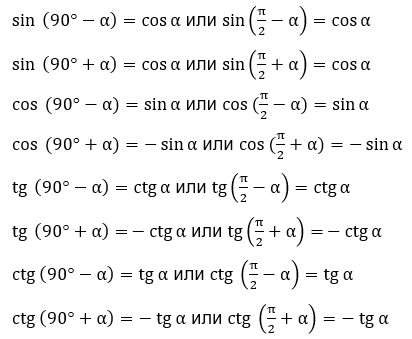
2) Формулы приведения с опорной точкой 180° или π:
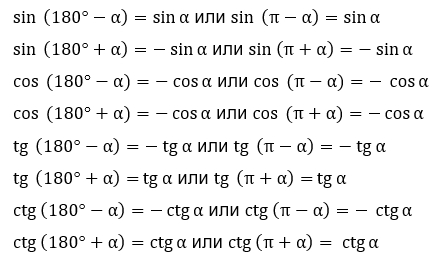
3) Формулы приведения с опорной точкой 270° или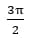 
:
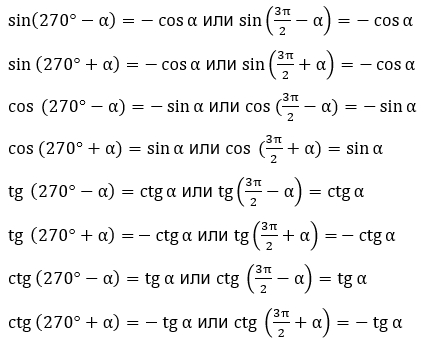
4) Формулы приведения с опорной точкой 360° или 2π:
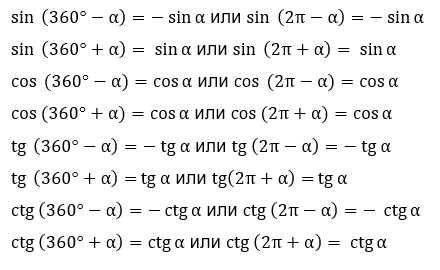
Доказательства формул
Чтобы убедиться в том, что формулы правильные и ими можно оперировать, докажем их. Но для этого надо вспомнить формулы сложения и вычитания для синуса и косинуса:
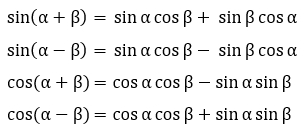
Не будем доказывать все 32 формулы приведения, возьмем по одной из каждого вида с разными тригонометрическими функциями:
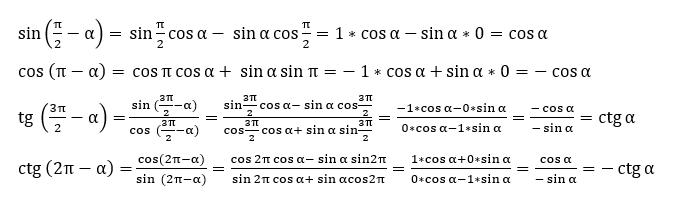
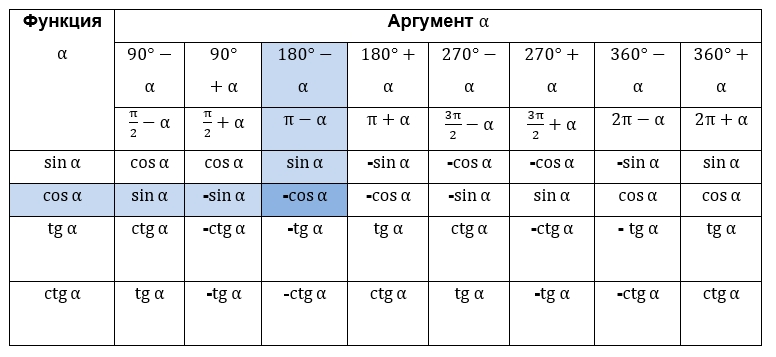
Таблица формул приведения
Для того чтобы воспользоваться этой таблицей, выберите строку с нужной функцией и столбец с необходимым аргументом — их пересечение укажет на ответ. Например, cos(180° - α) = -cosα
Таблица приведения
Как запомнить формулы приведения
Несмотря на то, что формул приведения целых 32 штуки и выше мы привели компактную таблицу, все же заучивать все формулы наизусть нет необходимости, а таблицей не всегда удобно пользоваться. Существует простой закон, которому подчиняются все формулы приведения и который поможет написать любую из них в нужный момент. Этот закон еще называют мнемоническим алгоритмом. Он состоит из 2-х правил:
- Первое, что нужно сделать, - определить знак функции в соответствующей четверти, причем знак определяется у исходной функции. Важно запомнить рисунок снизу: в каких четвертях и какая тригонометрическая функция имеет знак «-» или «+».Например,
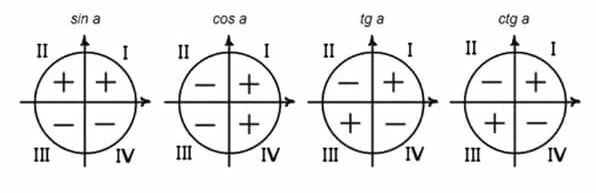
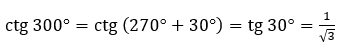– угол 30° находится в I четверти, а тангенс в I четверти положительный, соответственно, и ответ со знаком «+». - Запомнить, что при опорных точках 90° и 270° функция меняется на кофункцию, а при 180° и 360° - функция остается неизменной. Это значит, что при одном условии синус меняется на косинус, а тангенс – на котангенс, и наоборот.
Это правило еще именуют правилом лошади. В давние времена жил математик, склонный к рассеянности, который при поиске ответа менять или не менять название функции (например, синус на косинус), смотрел на свою умную лошадь. Она кивала головой вдоль той оси координат, которой принадлежала опорная точка: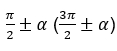 
или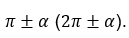 
Если лошадь кивала головой вдоль оси ОУ, то математик считал, что лошадь отвечает ему «да, менять», если же вдоль оси ОХ, то – «нет, не менять».
Например,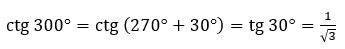 
– так как у нас опорная точка 270°, котангенс изменился на тангенс.
FAQ
Как запомнить все формулы?
Чтобы легче было выучить и применять все формулы нужно запомнить:
- рисунок, на котором указано в каких четвертях находится та или иная функция и какой знак имеет;
- функция меняется на кофункцию в 90° и 270°. Проще говоря, синус на косинус, а тангенс на катангенс;
- при значении углов 180° и 360° функция не меняется.
Как определить знак функции в ответе?
Определить знак функции в ответе можно по рисунку, который привели выше. Определите в какой четверти находится значение функции и поставьте нужный знак. Обратите внимание, что для каждой функции свой рисунок.
Где это пригодиться?
Знание темы пригодится для сдачи ОГЭ по итогам окончания 9 класса. В 10 классе изучение темы продолжают, чтобы выпускники в 11 классе смогли выполнить задания на ЕГЭ, где есть задачи и уравнения по тригонометрии (определить угол, решить тригонометрические выражения, задачи на касательную и т.д.), а именно 7 и 13 задания.
Какие ошибки чаще всего допускают при использовании формул приведения?
Согласно заключению ФИПИ по итогам ответов выпускников предыдущих лет, при решении заданий допускают ошибки:
- в применении формул приведения (неправильно определен знак тригонометрической функции или не изменили либо, наоборот, изменили на кофункцию при отсутствии потребности в этом);
- неправильное использование тригонометрических формул (вместо формулы приведения используется формула сложения и др.);
- неверное решение простейших тригонометрических уравнений, то есть неверно определен синус, косинус, тангенс или котангенс угла (табличные значения).
Формулы приведения предназначены для того, чтобы привести тригонометрическую функцию произвольного угла к тригонометрической функции острого угла с целью упростить сложные тригонометрические выражения или полностью решить уравнения. Данные формулы используются не только в математической науке, включая алгебру, геометрию и тригонометрию, но и, как правило, в физике, инженерии, и даже экономике. Поэтому формулы приведения вам пригодятся как на экзамене, так и в вашей будущей профессии, если вы свяжете свое будущее с математикой.