Расстояние, время и скорость в математике

Расстояние, время и скорость – это фундаментальные математические понятия. С их помощью описываются и решаются простые задачи, которые встречаются в повседневной жизни. Но понимание той тесной взаимосвязи, в которой находятся эти меры, необходимо и при более сложных расчётах в математике, а также во множестве смежных областей науки и техники.

Расстояние

Расстояние – это протяжённость пути между 2 объектами, выраженная численно. А, говоря строго математическим языком, это протяжённость линии между 2 точками. Расстояние выражается с помощью мер длины, в большинстве случаев в метрах (м) и километрах (км).

Например, можно сказать, что расстояние между школой и бассейном составляет 130 м, а между городами Москвой и Санкт-Петербургом – от 650 до 720 км в зависимости от выбранного маршрута.

Расстояние обозначается латинской буквой s и выражается как произведение скорости (v) и времени (t):

Время

Время – это продолжительность событий, выраженная численно. А, говоря строго математически языком, это непрерывная цепь событий, которые происходят последовательно от прошлого к будущему. Время – измеримая величина, она выражается в секундах (с), минутах (мин), часах (ч), сутках и пр.

Например, можно сказать, что от школы до бассейна ученик доходит пешком за 2 минуты, а от дома до дачи – его родители доезжают на автомобиле за 3 часа.

Время обозначается латинской буквой t и выражается через отношение расстояния (s) и скорости (v):

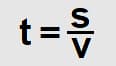
Скорость

Подробно познакомившись с простыми понятиями расстояния и времени, мы может перейти к изучению более сложной концепции скорости.

Скорость – это расстояние, которое объект преодолевает за единицу времени. Выражаясь математическими терминами, это отношение расстояния ко времени. Соответственно, скорость измеряется в единицах зависимых величин, например, в метрах в секунду (м/с), в километрах в час (км/ч) и пр.

Например, можно сказать, что ученик идёт от школы к бассейну со скоростью 65 м/мин, а его родители едут от дома до дачи со скоростью 60 км/ч.

Скорость обозначается латинской буквой v и выражается через отношение расстояния (s) и времени (t):

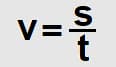
Скорость сближения и удаления

На практике часто приходится рассчитывать не только скорости отдельных объектов, но также скорости их сближения и удаления. Здесь сближением называют движение объектов навстречу друг другу, а удалением – движение в противоположных направлениях.

Скорость сближения – это расстояние, преодолеваемое объектами за единицу времени при движении навстречу друг другу. Она равна сумме всех скоростей. Таким образом, при движении объектов со скоростями v₁ и v₂ скорость сближения между ними составит:

Если объекты движутся вдогонку, то скорость сближения является разницей их скоростей:

Скорость удаления – это расстояние, преодолеваемое объектами за единицу времени при движении в противоположных направлениях. Она равна сумме всех скоростей. Таким образом, при движении объектов со скоростями v₁ и v₂ скорость удаления между ними составит:

Если объекты движутся в одном направлении, но с отставанием, то скорость сближения представляет собой разницу их скоростей:

Взаимосвязь между расстоянием, временем, скоростью

Расстояние, время и скорость находятся в тесной взаимосвязи, которую можно описать с помощью следующего треугольника:

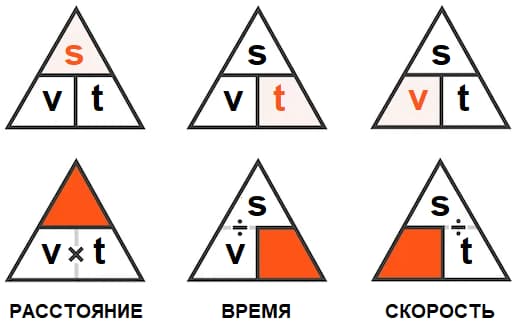
Чтобы найти любой из параметров, закройте его рукой, затем рассчитайте значение с помощью оставшихся величин. При выборе математической операции учитывайте простое правило: горизонтальная черта указывает на деление, вертикальная – на умножение.

Например, чтобы найти расстояние, перемножьте величины нижнего уровня: скорость и время. При расчёте времени разделите расстояние на скорость, а при расчёте скорости – расстояние на время.

Примеры решения задач

Задача №1. Расчёт скорости

Автомобиль проехал 5 км по шоссе за 5 минут, затем свернул на просёлочную дорогу и проехал ещё 8 км за 12 минут. Насколько снизилась его скорость на второй части пути?

Подробное решение:

1. Выразим минуты в часах.
   На первом отрезке пути автомобиль ехал 6 минут, на втором – 12 минут.
   Поскольку 60 минут составляют 1 час, то 6 минут эквивалентно 1/10, или 0,1 часа.
   Соответственно, 12 минут эквивалентно 1/5, или 0,2 часа.
2. Найдём скорость перемещения автомобиля по шоссе.
   v₁ = s₁/t₁ = 5/0,1 = 50 км/ч.
3. Найдём скорость перемещения автомобиля по просёлочной дороге.
   v₂ = s₂/t₂ = 8/0,2 = 40 км/ч.
4. Найдём, насколько изменилась скорость на второй части пути.
   v_Δ = v₁-v₂ = 50-40 = 10 (км/ч).

Ответ: 10 км/ч.

Задача №2. Расчёт скорости сближения

Автомобиль и автобус выехали из разных городов навстречу друг другу. Первый ехал со скоростью 80 км/ч, второй – 60 км/ч. Они встретились через 2 часа. Каково расстояние между населёнными пунктами?

Подробное решение:

1. Найдём путь, который проделал автомобиль за 2 часа.
   s₁ = v₁*t = 80*2 = 160 км.
2. Найдём путь, который проделал автобус за 2 часа.
   s₂ = v₂*t = 60*2 = 120 км.
3. Найдём расстояние между населёнными пунктами.
   s = s₁+s₂ = 160+120 = 280 км.

Ответ: 280 км.

FAQ

Как в математике обозначаются расстояние, время, скорость?

При обозначении расстояния, скорости и времени в математике традиционно используются прописные латинские буквы s, t и v соответственно.

Как запомнить формулы расстояния, времени, скорости?

Указанные параметры находятся в строго определённой зависимости. Чтобы быстро освоить формулы их расчёта, воспользуйтесь математическим треугольником «расстояние-время-скорость»:

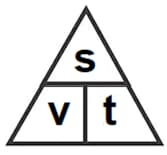
Здесь расстояние (s) находится на верхнем уровне, время (t) и скорость (v) – на нижнем. Закройте искомый показатель и рассчитайте его, пользуясь подсказками: если между оставшимися величинами горизонтальная черта – проведите операцию деления, если вертикальная – операцию умножения.

Вывод

Расстояние, время и скорость – это очень простые, но важные концептуальные понятия в математике. Школьники, начиная изучать и применять их на практике, часто путают формулы. Эту проблему важно решить быстро, и в этом помогает математический треугольник «расстояние, время, скорость».