Векторное произведение векторов

Понятие векторного произведения есть исключительно в трехмерном пространстве. На плоскости такой операции не существует. Данную тему школьники изучают в 11 классе. Тема непростая, но важная к изучению. К тому же на ЕГЭ могут быть подобные задания.

Что такое векторное произведение

Вектор – это направленный отрезок, у которого есть начало и конец, обозначенные точками. Отношение параллельных векторов называется коллинеарностью. 2 вектора будут коллинеарными, если они расположены на одной прямой или двух параллельных прямых, то есть они параллельны друг другу. Их направление может быть одинаковым или противоположным.

Прежде чем разобраться в понятии векторного произведения, стоит понять ориентацию всех упорядоченных групп векторов. Для этого в системе координат откладываем 3 вектора, идущих из одной точки. У двух из представленных векторов ориентация может быть правой или левой. Их направление напрямую связано с ориентацией самого вектора. В каком направлении будет расположен наиболее короткий поворот от двух векторов, а и b от вектора с? Если максимально короткий поворот проходит против часовой стрелки, то одновременно все 3 вектору окажутся правыми. И наоборот. Все 3 вектора будут левыми, если их движение направлено по часовой стрелке.

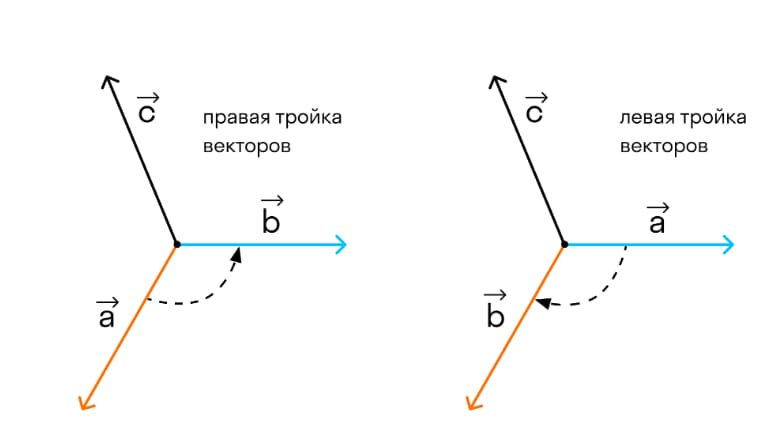
Возьмем неколлинеарные вектора →а и →b. От точки А отложим 2 вектора →АВ=→а и →АС=→b. Отдельно нарисуем вектор → АD=→с. Он будет одновременно перпендикулярным к векторам →АВ и →АС. Этот вектор может иметь разные направления. Исходя из этого, упорядоченная тройка векторов может быть левой или правой.

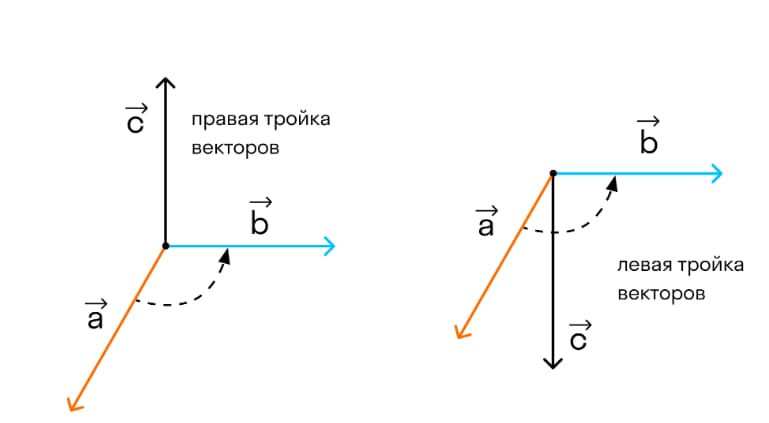
Векторным произведением векторов →а и →b, заданных в прямоугольной системе координат трехмерного пространства есть вектор →с:

• который является нулевым, при коллинеарности векторов →а и →b;
• который является одновременно перпендикулярным к векторам →а и →b;
• у которого длина векторного произведения равна произведению длин векторов →а и →b на синус угла между ними.

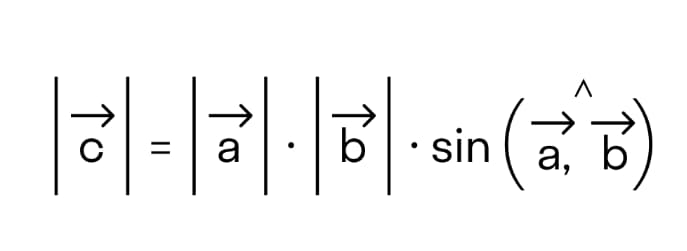
Тройка векторов →а, →b и →с будут ориентированы также, как и имеющаяся система координат.

Векторное произведение вектора →а на →b – вектор →с, длина которого равняется площади параллелограмма, который можно построить на векторах →а и →b, перпендикулярный к их плоскости и направленный таким образом, чтобы минимальное вращение от →а до →b вокруг →с, происходило против часовой стрелки, относительно конца вектора →с.

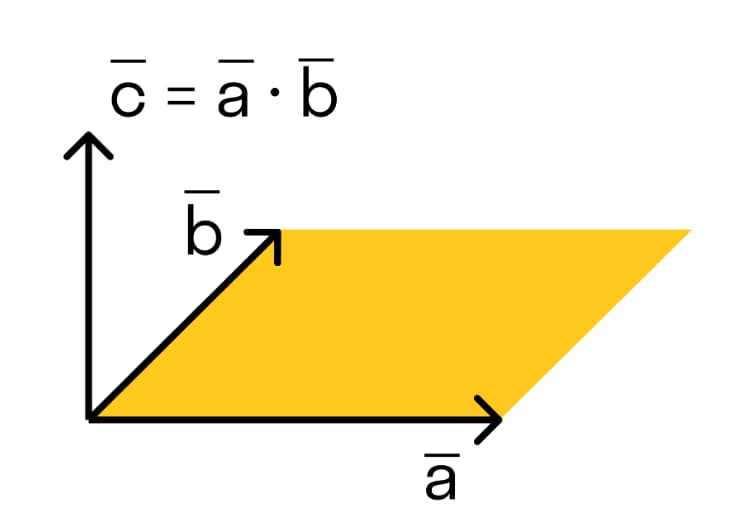
Векторное произведение векторов a = {ax; ay; az} и b = {bx; by; bz} – это вектор, у которого можно вычислить значение по формуле:

Координаты векторного произведения

Как находить координаты векторного произведения, имея координаты заданных векторов?

Векторное произведение векторов →a = (ax, ay, az) и →b = (bx, by, bz) в прямоугольной системе координат трехмерного пространства – это вектор

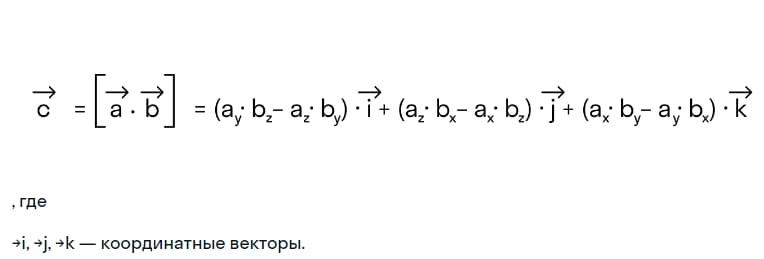
Векторное произведение удобнее представлять в форме квадратной матрицы третьего порядка, где первой строкой будут орты →i, →j, →k, второй – координаты →а, а третьей координаты →b.

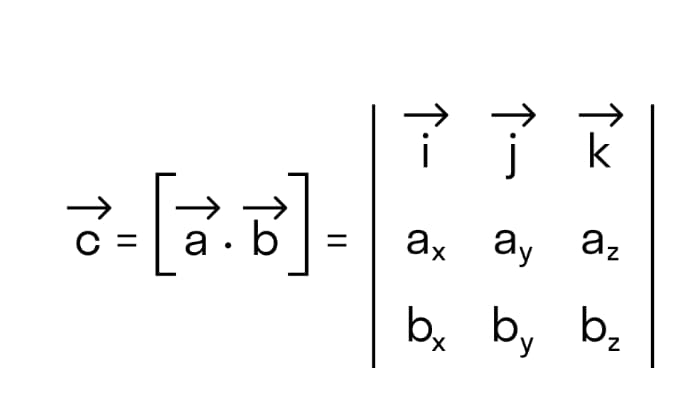
Разделив определитель на элементы первой строки, имеем равенство:

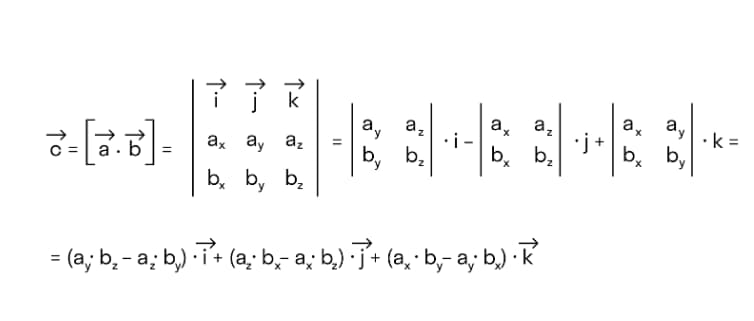
Свойства векторного произведения

В координатной системе векторное произведение имеет вид определителя матрицы:

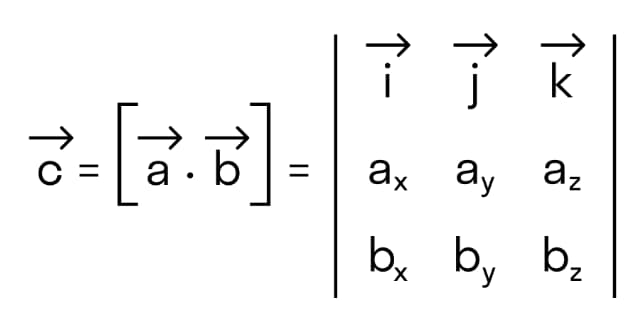
Исходя из свойств определителя, вытекают свойства векторного произведения:

1. Антикоммутативность
   
   
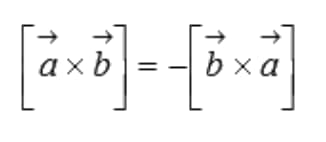
2. Дистрибутивность
   
   
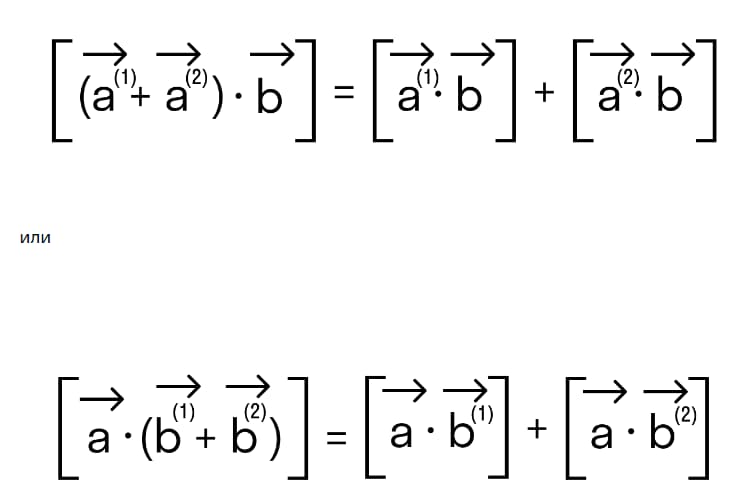
3. Сочетаемость
   
   

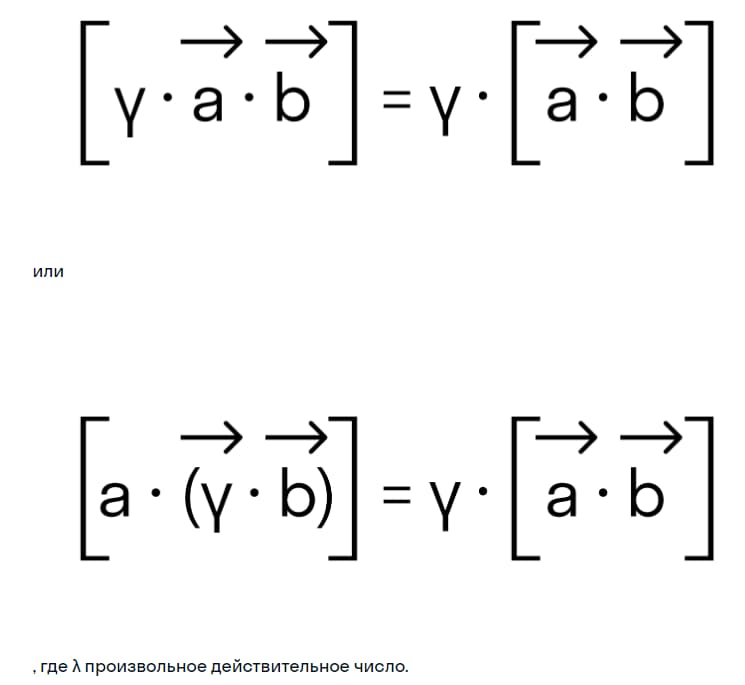
Докажем антикоммутативное свойство векторного произведения.

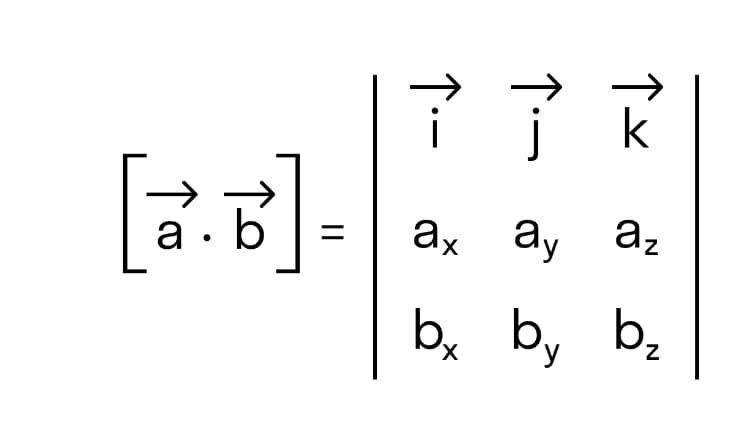
и

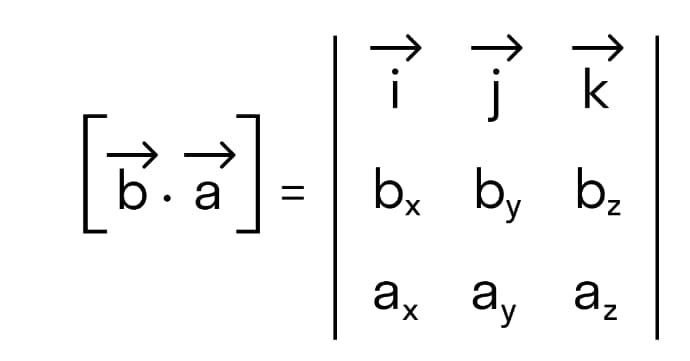
Исходя из того, что если переставить две строчки местами, значение определителя матрицы меняется на противоположное, получаем

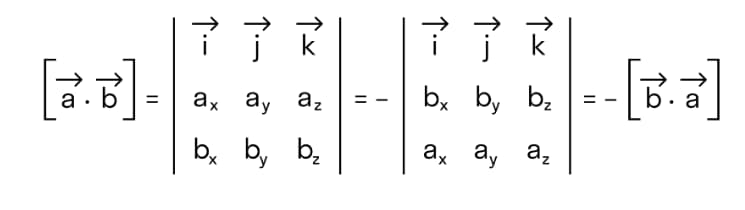
Разберем примеры – задачи и решение

FAQ

Чем отличается скалярное произведение от векторного произведения векторов?

Разница состоит в том, что результатом скалярного произведения является число, а векторного – вектор.

Какие вектора называют компланарными?

Компланатрные вектора – это вектор или вектора, расположенные на одной плоскости или параллельные ей.

В чем геометрический смысл векторного произведения?

Векторное произведение имеет перпендикулярное направление к плоскости, которая проходит через вектор-сомножитель. По модулю оно равно площади параллелограмма, который построен на этих векторах.

Вывод

Векторное произведение векторов используют, когда необходимо проверить несколько векторов на перпендикулярность или исследовать угол между ними. Векторы могут использоваться не только в математике, но и физике (импульс, скорость, сила могут быть представлены в виде векторных величин).