Уравнение касательной к графику функции
Уравнениями касательной графику функции занимаются в 10 классе общеобразовательной школы. Уравнение касательной позволяет определить точное положение касательной линии в заданной точке графика функции.
Мы расскажем, как составить уравнение касательной к графику функции, геометрический смысл производной, приведем задачи с решениями.
Геометрический смысл производной
Геометрический смысл производной заключается в определении скорости изменения функции в каждой точке графика. Если производная положительна, то функция возрастает в данной точке, а если производная отрицательна, то функция убывает. Также нулевое значение производной указывает на точку экстремума функции - либо максимум, либо минимум.
Определение геометрического смысла производной:
- Возьмем произвольную функцию y = f(x) и обозначим на ней точку А с координатами (x0;f(x0)) и точку В с координатами (x0+Δx;f(x0+Δx)
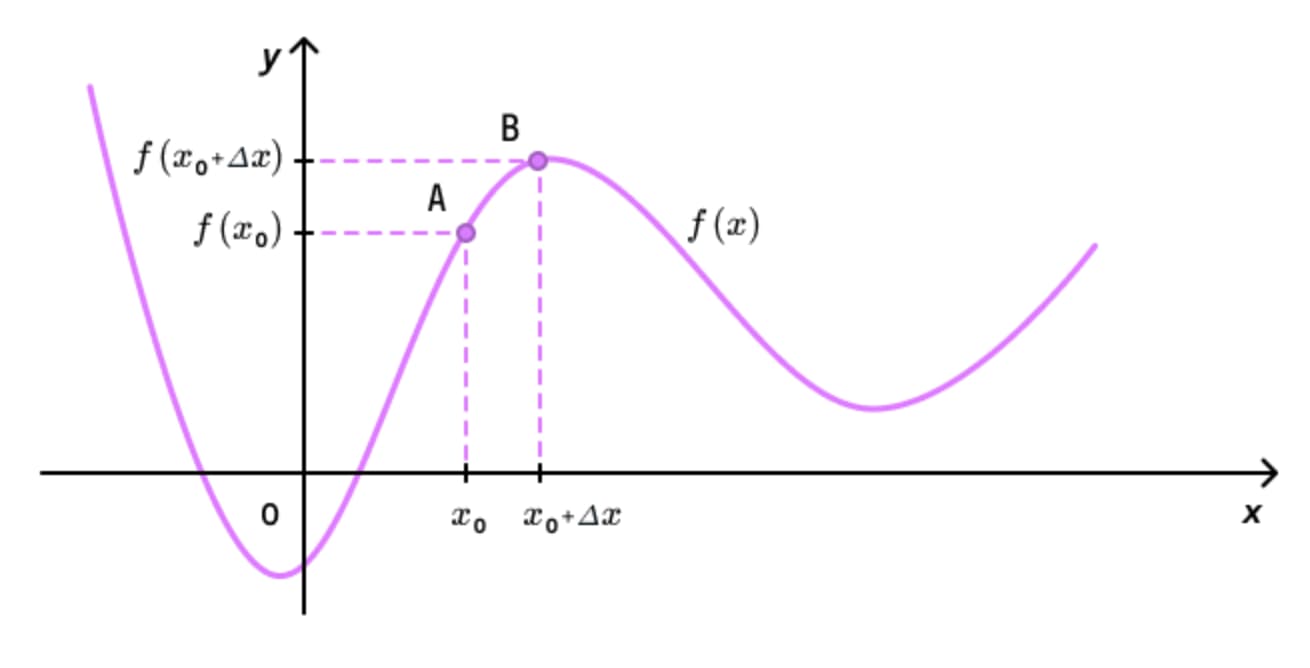
- Через точки А и В проведем прямую.
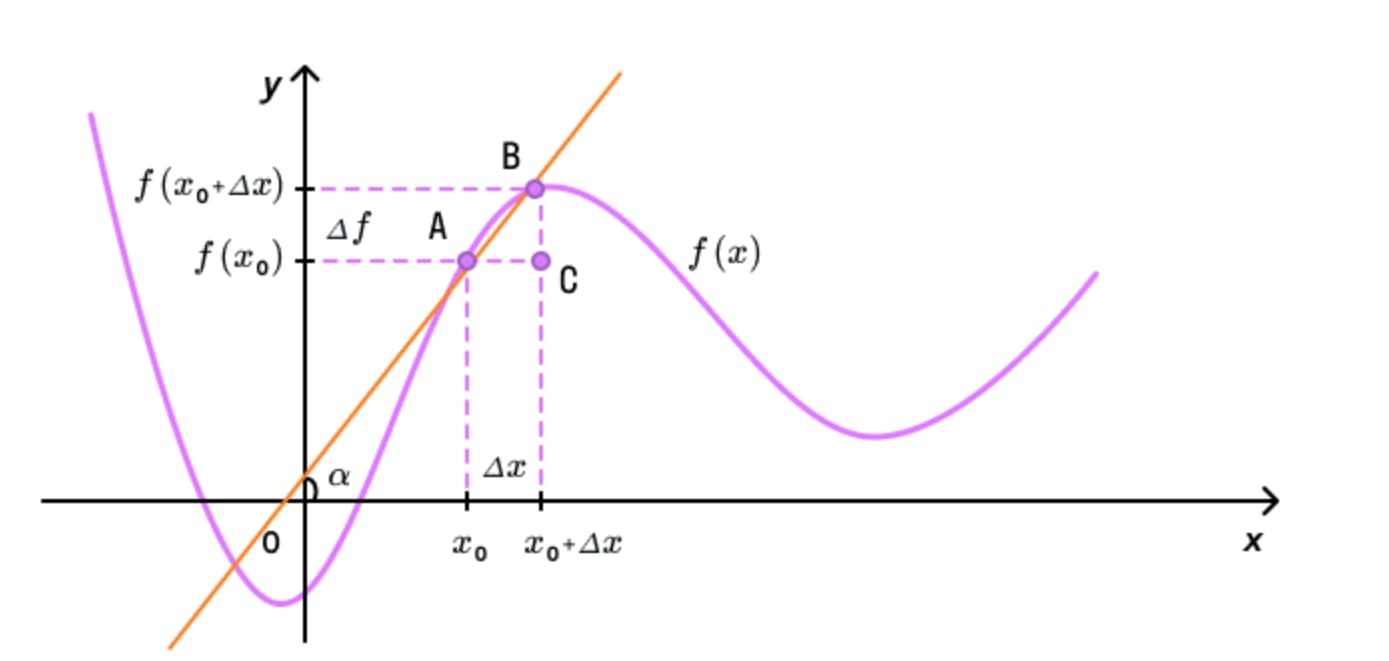
- Угол α будет наклона прямой к оси абсцисс.
- Через точку А проводим прямую, параллельно оси абсцисс, а через точку B — прямую, параллельно оси ординат (прямые y и х). Точку пересечения прямых обозначим как С.
- Получаем прямоугольный треугольник АВС, в котором катет AC = Δ x, катет BC=Δf.
- Возьмем отношения этих значений Δf/Δx и получим отношение противолежащего катета к прилежащему катету, что равно tgα.
- При уменьшении расстояния между точками A и B, как следствие будут уменьшаться длины отрезков Δx и Δf и в какой-то момент точка В совпадет с точкой A, а отношение Δ/fΔx станет равно производной функции y = f(x) в точке x
- Касательная — это прямая с уравнением y = kx + b, где k — это коэффициент наклона прямой, который равен тангенсу угла между прямой и осью абсцисс.
- Отсюда k = tgα=f′(x0).
Разберем примеры – задачи и решение
Разберем несколько задач.
Задача №1
Дан график функции 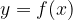 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой 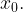 Найдите значение производной функции
Найдите значение производной функции 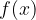 в точке
в точке 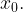
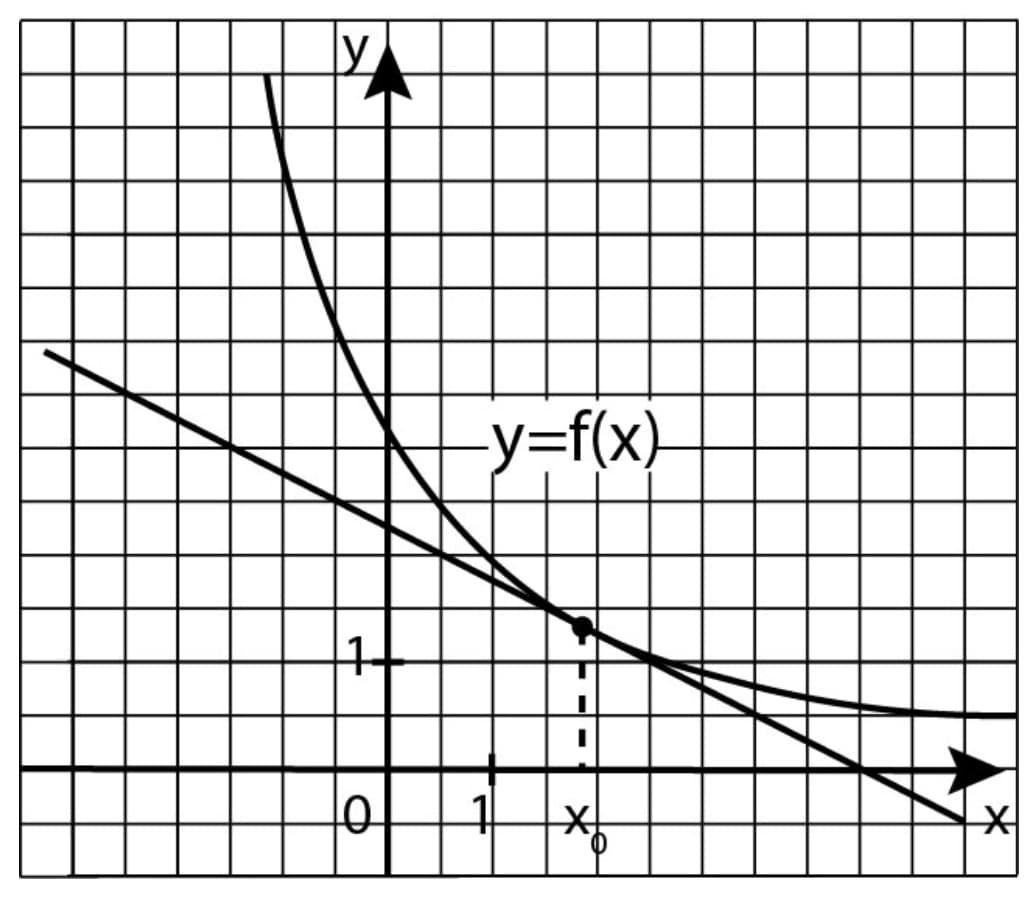
Решение:
Геометрический смысл производной:
Производная функции в точке равна тангенсу угла наклона касательной, проведенной к графику функции в этой точке (то есть угловому коэффициенту касательной).
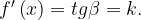
В точке 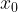 функция y = f(x) убывает. Касательная, проведенная к ее графику в этой точке, образует тупой угол
функция y = f(x) убывает. Касательная, проведенная к ее графику в этой точке, образует тупой угол 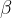 с положительным направлением оси Х. Найдем тангенс острого угла
с положительным направлением оси Х. Найдем тангенс острого угла 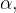 смежного с углом
смежного с углом 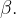
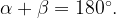
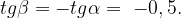
Ответ: -0,5.
Задача №2
К графику функции y = f(x) проведена касательная в точке с абсциссой x0. Требуется найти угловой коэффициент касательной к графику функции.
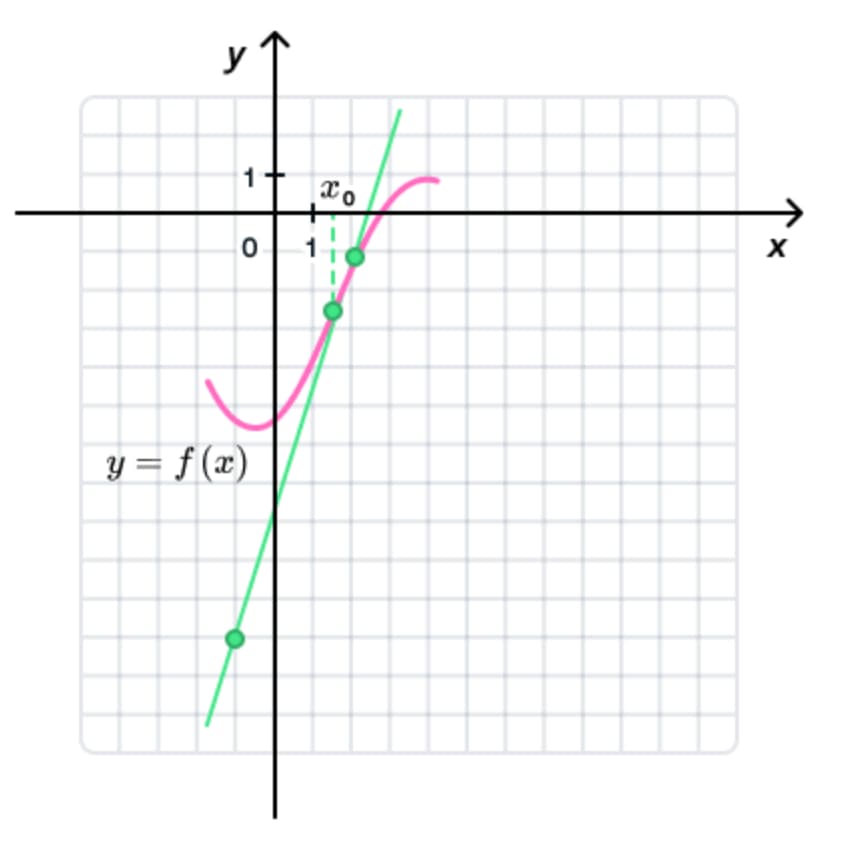
Найдем угловой коэффициент касательной, который равен тангенсу угла наклона касательной к графику функции в точке. На прямой построим прямоугольный треугольник и найдем отношение противолежащего катета к прилежащему:10/3»3
Ответ: 3
Как составить уравнение касательной к графику функции
Уравнение касательной к графику функции y = f(x) в точке x0:
y = f′(x0)(x−x0) + f(x0)
Алгоритм составления уравнения
Дано: уравнение кривой y=f(x), абсцисса точки касания x0.
Порядок выведения уравнения касательной:
- Найдем значение функции в точке касания f(x0).
- Найдем общее уравнение производной f'(x).
- Найдем значение производной в точке касания f'(x0).
- Запишем уравнение касательной y = f'(x0)(x - x0) + f(x0).
- Приведем уравнение к виду y = kx + b.
Пример:
Составьте уравнение касательной к графику функции 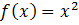 в точке с абсциссой
в точке с абсциссой  .
.
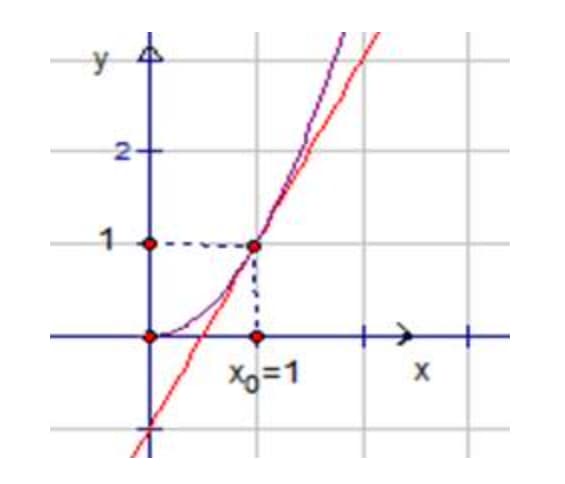
Порядок нахождения уравнения:
Для решения задачи поставим точку  . Значение функции в этой точке равно 1.
. Значение функции в этой точке равно 1.
Составим уравнение касательной к графику функции:
- Находим
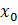 и точку касания.
и точку касания.
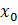 - дано, точка касания: (
- дано, точка касания: ( ;
;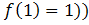 .
. - Находим производную в любой точке
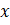 .
.
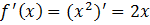 .
. - Находим значение производной в точке с абсциссой
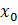 .
.
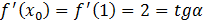 .
. - Уравнение касательной.
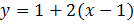 .
.
Упрощаем и получаем: 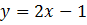 .
.
Ответ: уравнение касательной к графику функции в точке 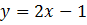 .
.
FAQ
Определение геометрического смысла производной?
Производная функции в точке равна тангенсу угла наклона касательной, проведенной к графику функции в этой точке (то есть угловому коэффициенту касательной).
Можно ли составить уравнение касательной к графику функции в заданной точке онлайн?
Да, есть специальные онлайн-калькуляторы, помогающие составлять уравнения, например, symbolab.com, mathforyou.net, math.semestr.ru
Вывод
- Касательная — это прямая с уравнением y = kx + b, где k — это коэффициент наклона прямой, который равен тангенсу угла между прямой и осью абсцисс, k = tgα=f′(x0).
- Уравнение касательной к графику функции y = f(x) в точке x0 формула:
y = f′(x0)(x−x0) + f(x0).
- Знание математической теории и опыт в составлении уравнений касательных, понимание геометрического смысла производной и умение решать задачи с помощью производных помогут создавать точные математические модели, описывающие изменения в различных ситуациях и анализировать их геометрическое значение.

