Умножение десятичных дробей

Умножение десятичных дробей важно, когда речь идёт о группировке элементов, например, при расчёте количества закупаемых товаров на несколько человек. Но эта математическая операция часто не столь проста в реализации, как кажется на первый взгляд. Чтобы провести её правильно, нужно понимать некоторые нюансы работы с десятичными числами.

Что такое десятичная дробь – понятие

В математике рассматриваются разные типы чисел, например, натуральные, целые, рациональные и пр. Среди них есть десятичные числа – стандартная форма представления целых и нецелых чисел.

Десятичная дробь представляет собой число, состоящее из целой и дробной частей, которые традиционно разделяют запятой (в англоязычных странах в качестве разделителя используется точка). В числовом ряду она располагается между соседними целыми числами и выражается, как числовое значение меньшей из этих чисел плюс некоторая часть целого.

Например, человек получает заработную плату в размере 34700 руб. Если выразить её в тысячах, то получится десятичное число: 34,7 тыс. руб.

Свойства десятичных дробей

Прежде чем научиться оперироваться десятичными числами, следует понять их суть. Они обладают всего 4 базовыми свойствами, которые очень просты и легко запоминаются:

1. Величина десятичной дроби останется прежней, если справа (после последней значащей цифры) вписать любое количество нулей. Например,
   0,35 = 0,350 = 0,3500000
2. Величина десятичной дроби останется прежней, если справа (после последней значащей цифры) зачеркнуть любое количество нулей. Например,
   0,3050 = 0,305
3. При смещении разделителя (запятой) вправо на 1, 2, 3… шагов величина десятичной дроби взрастает в 10, 100, 1000… раз. Например,
   0,558 x 100 = 55,8
4. При смещении разделителя (запятой) влево на 1, 2, 3… шагов величина десятичной дроби уменьшается в 10, 100, 1000… раз. Например,
   55,8 / 100 = 0,558

В расчётах с участием десятичных чисел используются стандартные математические законы и правила. На основании этого можно выделить ещё несколько важных свойствах:

1. Коммутативное: при сложении и умножении десятичных чисел их порядок не имеет значения. Например, 0,4 + 0,1 = 0,1 + 0,4 или 0,3 x 0,7 = 0,7 x 0,3.
2. Ассоциативное: при сложении и умножении перегруппировка чисел не приводит к изменению результата. Например, (0,4 + 0,3) + 0,8 = 0,4 + (0,3 + 0,8) или (0,4 x 0,3) x 0,8 = 0,4 x (0,3 x 0,8).
3. Распределительное: умножение десятичной дроби на сумму любых десятичных дробей аналогично её умножению на каждое число суммы с последующим сложением результатов (произведений). Например, 0,2 x (0,3 + 0,5) = 0,2 x 0,3 + 0,2 x 0,5.
4. Свойство идентичности: число 1 – это мультипликативное тождество десятичных дробей, а число 0 – аддитивное тождество. Например, 0,5 x 1 = 0,5 и 0,5 + 0 = 0,5.
5. Обратное свойство: каждая десятичная дробь имеет аддитивную обратную (противоположную) и мультипликативную обратную (обратную). Например, аддитивная инверсия 0,5 = -0,5, а мультипликативная инверсии 0,5 = 1/0,5 = 10/5.

Как записать десятичную дробь

На практике часто приходится записывать простые дроби в виде десятичных чисел. Чтобы делать это правильно, запомните простое правило: сначала указывается целое число, после которого ставится запятая и записывается дробная часть.

Например, нужно обыкновенную дробь 15⁄10 перевести в десятичную. В этом случае целой число равно 1, т.к. при делении числителя на знаменатель получается число больше 1, но меньше 2. После него ставим запятую и в дробную часть записываем остаток. Получается число: 1,5.

Как читать десятичную дробь

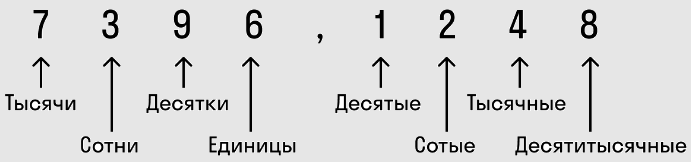
Существует правило, как правильно произносить десятичные дроби вслух. Сначала называют целую часть с упоминанием слова «целые», затем дробную – с упоминанием разряда числительного.

Чтобы запомнить разрядность десятичных дробей, используйте простую схему:

Умножение десятичных дробей

В целом процедура умножения десятичных чисел похожа на умножение целых чисел, за исключением размещения десятичной точки в произведении.

Умножение на целые числа

При умножении десятичной дроби на целое число в произведении ставится запятая с учётом того, сколько цифр в дробной части первого числа.

Алгоритм выполнение математической операции:

1. Умножьте 2 числа обычным способом (в столбик), игнорируя разделитель.
2. Получив результат, поставьте разделитель, отсчитав то же количество десятичных знаков, что и в десятичном числе (одном из множителей).

Умножение на числа, кратные 10

Умножение любой десятичной дроби на 10, 100, 1000… (возведение в степень 10, 100, 1000…) просто сдвиньте разделитель (запятую) вправо на столько знаков, сколько нулей в числе, кратном 10. Например, при умножении десятичной дроби на 10 запятая сдвигается вправо на 1 шаг, на 1000 – на 3 шага и т.д.

Умножение двух десятичных дробей

Это то же самое, что и для целого числа, но с той лишь разницей, что при этом мы должны взять сумму общего количества десятичных знаков в обоих данных числах, которая должна быть равна количеству десятичных знаков в продукт . Чтобы умножить две десятичные дроби, выполните действия, перечисленные ниже:

Алгоритм выполнение математической операции:

1. Умножьте 2 числа обычным способом (в столбик), игнорируя разделитель.
2. Получив результат, поставьте разделитель, отсчитав то количество десятичных знаков, равное общему количеству десятичных знаков в обоих множителях.

Разберем примеры – задачи и решение

Задача №1. Умножение на целое число

Студенты решили сделать вклад в один из благотворительных фондов. Каждый из них внёс по 1,5 тыс. руб. Какова общая сумма вклада, если в учебной группе числится 24 студента?

Решение:

Находим общую сумму, которую студенты внесли в фонд:

1,5 x 24 = 36 (тыс. руб.)

Результат получен путём умножения десятичной дроби на целое число:

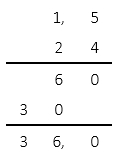
Ответ: общая сумму вклада студентов учебной группы в благотворительной фонд составила 36 тыс. руб.

Задача №2. Умножение на числа, кратные 10

По результатам любительской велогонки по бездорожью было установлено, что средняя скорость спортсмена, пришедшего последним, составила всего 3,4 км/ч. Скорость победителя оказалась выше в 10 раз. Определите, чему она равна.

Решение:

Находим, чему равна скорость победителя велогонок:

3,4 x 10 = 34 (км/ч)

При умножении десятичной дроби на число, кратное 10, результат получают простым перемещением запятой вправо. При этом количество шагов равно количеству нулей в этом числе.

Ответ: скорость победителя любительских велогонок составила 34 км/ч.

Задача №3. Умножение двух десятичных дробей

Средняя скорость вращения Луны вокруг Земли по эллиптической орбите составляет 1,023 км/с. Какой путь пройдёт естественный спутник нашей планеты за 3,5 с?

Решение:

Находим расстояние, которое пройдёт Луна за 3,5 с:

1,023 x 3,5 = 3,5805 (км)

Результат получен путём умножения десятичных дробей:

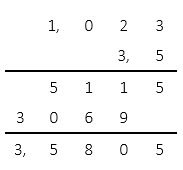
Ответ: за 3,5 с Луна пройдёт по околоземной орбите путь протяжённостью 3,5805 км.

Онлайн-калькуляторы – обзор

На первом этапе обучения при умножении десятичных дробей школьники часто испытывают трудности. Чтобы подтверждать свои результаты, им рекомендуется использовать современные специализированные калькуляторы (онлайн). Наиболее эффективные программы размещены на сайтах:

• https://web-calculator.ru/kalkulyator-drobej;
• https://calculator-drob.ru/calc/decimal-fraction.html;
• https://ru.onlinemschool.com/math/assistance/fraction/fraction_calc/.

FAQ

Легко ли научиться умножать десятичные числа?

В целом это простая тема. Однако статистика показывает, что и школьники, и студенты испытывают фундаментальные трудности при проведении математических операций с десятичными дробями. И это большая проблема, поскольку такие вычисления широко используются в практических ситуациях.

Причиной трудностей в освоении материала являются неполное понимание значения десятичных дробей. Если Вам сложно понять, как работать с такими числами, разберите тему с учителем.

Вывод

Умножение десятичных дробей – простая математическая операция, при освоении которой большинство учеников 5 классов не испытывают трудностей. В этой теме важно понять свойства десятичных чисел и научиться правильно разграничивать целую и дробную части.