Треугольник – как найти площадь треугольника?

Треугольник входит в число самых распространенных геометрических фигур. Расчет его площади требуется не только для получения высокой оценки в школе, но и для решения множества практических задач. Причем в самых разных видах деятельности, включая проектирование, инженерию, дизайн одежды, конструирование и множество других. Рассмотрим более внимательно, как найти площадь треугольника, какие формулы для этого используются и как выбрать подходящую.

Основные определения

Треугольником называют плоскую геометрическую фигуру, которая образована из трех отрезков, соединяющих три точки, не расположенные на одной прямой. Точки являются вершинами, а отрезки – сторонам треугольника.

Площадь представляет собой пространство внутри границ геометрической фигуры. Она выражается количественно в специальных единицах измерения – квадратных миллиметрах, сантиметрах и т.д. Площадь входит в число основных численных характеристик любой фигуры, включая треугольник. Поэтому ее расчет выступает обязательным элементом математического анализа.

Важно добавить, что площадь треугольника относится к числу базовых параметров и понятий геометрии в целом. Поэтому тема статьи имеет настолько серьезное значение для всей школьной программы.

Формулы расчета площади треугольника

Классификация треугольников позволяет выделить несколько их видов. В зависимости от размеров и соотношения сторон они бывают разносторонними, равносторонними и равнобедренными. В зависимости от величины углов различают остро-, тупо- и прямоугольные треугольники.

Площадь фигуры определяется с использованием разных формул. Некоторые из них подходят для любых треугольников, другие – только для треугольников определенного вида. Что необходимо учитывать при выборе подходящей формулы для расчета.

Площадь любого треугольника рассчитывается следующим образом:

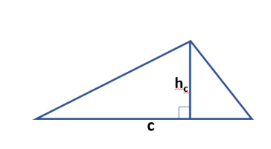
1. По стороне и высоте, опущенной на нее: S = ½ *c * h_c.
   
   
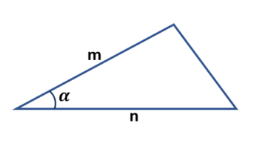
2. По двум сторонам и расположенному между ними углу: S = ½ * m * n * sin α.
   
   
3. По формуле Герона (по трем сторонам):
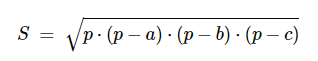   , где
   P – периметр (P = а + b + с);
   p – полупериметр (p = P/2).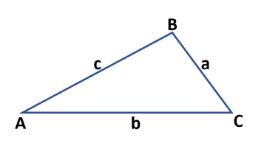
   
   
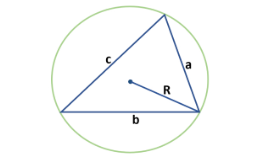
4. По трем сторонам и окружности, описанной вокруг треугольника: S = а * b * c /(4R).
   
   
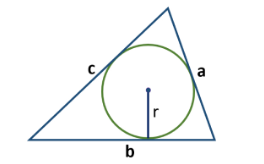
5. По полупериметру и радиусу окружности, вписанной в треугольник: S = p*r (правила расчета p показаны выше).
   
   

Площадь прямоугольного треугольника рассчитывается по формуле: S = ½ * а * b.

Формула является следствием приведенной выше для любого треугольника (по двум сторонам и углу между ними). В данном случае задействует прямой угол, синус которого равняется 1. Что позволяет убрать его из расчета и сделать формулу намного более простой и удобной для практического применения.

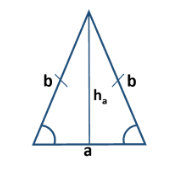
Площадь равнобедренного треугольника определяется так: S = ½ * b² * sin α. В расчете используется та сторона, которая имеет аналог (то есть не основание), и угол, расположенный между ними. Альтернативная формула вычисления площади подобной фигуры применяется, если даны основание и опущенная на него высота. В этом случае S = ½ * а * h_a.

Онлайн-калькуляторы

Расчет площади треугольника в большинстве случаев не относится к числу сложных задач. Что вовсе не означает необходимости производить его вручную. Сегодня можно найти множество специализированных или универсальных онлайн-калькуляторов, способных выполнить подобные вычисления в автоматическом режиме. В качестве примеров можно привести следующие сервисы:

• https://ru.onlinemschool.com/math/assistance/figures_area/triangle1/. Определяет площадь треугольника по трем сторонам, то есть классической формуле Герона;
• https://www.calc.ru/ploshchad-treugolnika.html. Универсальный калькулятор, предлагающий рассчитать площадь любого треугольника, причем разными способами на выбор пользователя;
• https://24calc.ru/ploshhad-treugolnika/. Онлайн-сервис с набором возможностей, полностью аналогичным описанному в предыдущем пункте списка. Выступает частью обширной платформы, на которой размещены самые разные калькуляторы;
• https://skysmart.ru/calculators/ploshad-treugolnika. Простой и удобный сервис для расчета площади треугольника тремя основными способами: по трем сторонам, по двум сторонам и углу между ними, по стороне и опущенной на нее высоте.

Важным достоинствами всех перечисленных и большинства подобных онлайн-калькуляторов выступает их доступность. Необходимые пользователю вычисления выполняются не только полностью бесплатно, но даже не требуют регистрации на сайте.

FAQ

Когда нужно вычислить площадь треугольника?

Задача решается как для получения высокой оценки (или экзаменационного балла на ЕГЭ), так и в практических целях (разными специалистами: проектировщиками, дизайнерами, инженерами, конструкторами и т.д.)

Чему равна площадь треугольника?

Для расчета искомой величины используются разные формулы. Самой распространенной считается вычисление площади треугольника по 3 сторонам (так называемая формула Герона).

Что нужно учесть при выборе формулы расчета площади треугольника?

Выбор оптимального способа расчета зависит от двух базовых параметров: известные исходные данные и разновидность треугольника.

Вывод

1. Треугольник – очень распространенная геометрическая фигура.
2. Необходимость найти его площадь возникает как в рамках школьного обучения, так и при решении практических задач в работе проектировщиков, инженеров, дизайнеров и множества других специалистов.
3. Расчет площади треугольника допускает использования различных формул: по трем сторонам, по двум сторонам и расположенному между ними углу и т.д.
4. Выбор подходящей формулы зависит от наличия исходных данных и разновидности треугольника.