Теория вероятностей

Теория вероятностей лежит в основе современной актуарной и финансовой математики, научных исследований разного уровня. Она позволяет вычислять возможность наступления событий, использовать полученные сведения в построении прогнозов и принятии решений во всех областях. Чтобы понять её сущность и начать использовать в решении практических задач, необходимо освоить базовые понятия: события и их типы, алгебру событий, классическое определение вероятности.

Онлайн-калькуляторы для расчёта вероятности события – обзор сервисов

Начиная изучать теорию вероятности, ученику полезно иметь под рукой инструмент, позволяющий быстро проводить математические вычисления и сверять полученные результаты со своими. В интернете есть множество калькуляторов для расчёта вероятности события; вот наиболее полезные из них:

1. Корпоративный портал «Томский политех». Здесь представлено 2 варианта калькуляторов: простой и профессиональный. Первые позволяет быстро рассчитать вероятность события по классической формуле, второй – производить более сложные расчёты. Обе программы имеют строгий, интуитивно понятный интерфейс с пояснениями.
2. Calculator Online. Сервис предоставляет простой калькулятор, с помощью которого можно рассчитать вероятности разного типа, например, единичную, условную, множества событий и пр. Его можно установить на мобильный телефон.
3. Statistics Kingdom (на английском языке). Здесь находится простой, но многофункциональный онлайн-калькулятор вероятности. Здесь можно не только выполнить простейшие расчёты, но и увидеть каждый шаг вычисления. При использовании классических формул из алгебры событий автоматически генерируются диаграммы Эйлера-Венна, которые помогают ученикам понять алгоритмы расчётов и усвоить основную терминологию.

Теория вероятностей – основные понятия

Теория вероятностей – это раздел математики, изучающий анализ случайных событий. Она основывается на систематическом исследовании случайного эксперимента – математической модели реального опыта, результаты которого заранее неизвестны.

Классическим примером случайного эксперимента является бросок игральной кости: бросающий не знает число, которое выпадет. Исследование предполагает визуализацию всех возможных вариантов и осознание того, что они непредсказуемы. Но, исходя из характера испытаний и прошлых результатов (если имеются), можно определить вероятность наступления каждого из событий.

Событие: определение и виды

Центральным понятием в теории вероятностей является событие, которое представляет собой набор результатов (подмножество выборочного пространства) случайного эксперимента.

Сразу важно понять, что выборочное пространство – это весь спектр исходов, возможных при проведении опыта. Например, при одновременном подбрасывании 3 монет вероятны такие результаты:

S = {(A₀, A₀, A₀), (A₀, A₀, A̅₀), (A₀, A̅₀, A₀), (A̅₀, A₀, A₀), (A₀, A̅₀, A̅₀), (A̅₀, A₀, A̅₀), (A̅₀, A̅₀, A₀), (A̅₀, A̅₀, A̅₀)}, где

S – выборочное пространство;

A₀ – событие, при котором монета выпадает «орлом»;

A̅₀ – событие, при котором монета выпадает «решкой».

Выборочное пространство состоит из множества элементарных событий A₀ и A̅₀. Но если нужно учесть только некоторые результаты, например, при которых выпадает «решкой» 2 и более раз, то набор возможных вариантов изменится:

E = {(A₀, A̅₀, A̅₀), (A̅₀, A₀, A̅₀), (A̅₀, A̅₀, A₀), (A̅₀, A̅₀, A̅₀)}, где

E – событие, являющееся подмножеством выборочного пространства S;

A₀ – событие, при котором монета выпадает «орлом»;

A̅₀ – событие, при котором монета выпадает «решкой».

Классификация событий

В рамках случайного эксперимента может существовать только одно выборочное пространство, но множество событий разных типов. Вероятность наступления каждого из них лежит в области от 0 до 1; и в зависимости от принимаемого значения выделяют говорить 3 класса событий:

1. Достоверные (неизбежные) – это события, которые гарантированно произойдут при соблюдении определённых условий. Например, после зимы наступит весна, а при подбрасывании классической игральной кости выпадет число менее 7. Подобные события обозначаются символом Ω, а вероятность их наступления равна 1.
2. Невозможные – это события, которые заведомо не могут произойти в ходе эксперимента. Например, невозможно, что вода в реке замёрзнет при температуре воздуха +35°C и выше, а при подбрасывании монета зависнет в воздухе. Такие события обозначаются символом ∅, а вероятность их наступления равна 0.
3. Случайные (равновероятные) – это события, которые могут произойти или не произойти в каждом из испытаний в рамках эксперимента. Например, при подбрасывании монеты обязательно выпадет «орёл» или «решка». Вероятность наступления таких событий больше 0, но меньше 1.

Принято говорить, что событие E выборочного пространства S произошло, если результат ω эксперимента таков, что ω ∈ E и не произошло – если ω ∉ E.

Алгебра событий

В рамках случайного эксперимента разные события могут появляться одновременно. Например, при подбрасывании игральной кости событие A означает выпадение числа 5, а B – выпадение нечётного числа. Чтобы оперировать разными данными и выстраивать логичные рассуждения, в теории вероятностей используются математические операции. Они составляют основу алгебры событий.

Базовыми операциями являются объединение и пересечение событий. В первом случае получают , включающие включает результаты, которые происходят в любом из событий, тогда как пересечение событий включает результаты, которые происходят в обоих событиях.

Объединение событий: сложение

Событие «A или B» предполагает наступление хотя бы одного из событий A и B и представляет собой объединение (сумму) множеств A и B. На практике оно обозначается как A ∪ B, или A + B. Следовательно, событие «A или B» = A ∪ B = {ω: ω ∈ A или ω ∈ B}.

Объединение 2 множеств наглядно представлено на схеме «Эйлера-Венна»:

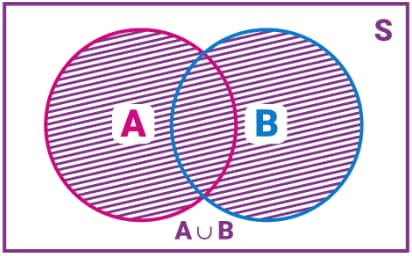
Например, испытание предполагает подбрасывание 2 игральных костей одновременно. Выборочное пространство можно записать как:

S = {(1, 1), (1, 3), (2, 5), (5, 5), (2, 2), (1, 2), (2, 1), (2, 2) , (2, 3), (2, 1)}

Пусть A – это событие получения общей суммы очков, равной 3; а B – это событие получения одинаковых очков на обеих игральных костях. Тогда результатами испытаний являются:

А = {(1, 2), (2, 1), (2, 1)}

B = {(1, 1), (5, 5), (2, 2), (2, 2)}

Теперь можно записывать сумму множеств:

A ∪ B = {(1, 1), (1, 2), (2, 1), (2, 1), (2, 2), (2, 2), (5, 5)}

Пересечение событий: умножение

Событие «A и B» предполагает одновременное наступление обоих событий A и B и представляет собой пересечение (произведение) множеств A и B. На практике оно обозначается как A ∩ B, или AB. Следовательно, событие «A и B» = A ∩ B = {ω: ω ∈ A и ω ∈ B}.

Пересечение 2 множеств наглядно представлено на схеме «Эйлера-Венна»:

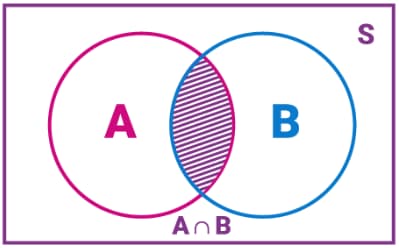
Например, испытание предполагает подбрасывание 2 игральных костей одновременно. Выборочное пространство можно записать как:

S = {(1, 5), (4, 6), (2, 1), (3, 5), (2, 3), (4, 2), (4, 4), (2, 2) , (2, 3), (6, 5)}

Пусть A – это событие получения общей суммы очков, равной 6; а B – это событие, когда на второй игральной кости фиксируется 5 очков. Тогда результатами испытаний являются:

А = {(1, 5), (4, 2)}

B = {(1, 5), (3, 5), (6, 5)}

Теперь можно записывать произведение множеств:

A ∩ B = {(1, 5)}

Классическое определение вероятности: формула

Согласно классическому определению, вероятностью (P) события A называют отношение числа (m) исходов испытания, благоприятствующих событию, к числу (n) равновозможных несовместных элементарных исходов, образующих полную группу. Формула вероятности записывается так:

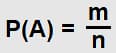
Вероятность обладает 2 постоянными свойствами:

• вероятность достоверного события приравнивается к 1;
• вероятность невозможного события приравнивается к 0;
• вероятность случайного события является положительным числом, лежащим между 0 и 1.

Таким образом, вероятность случайного события удовлетворяет неравенству:

Как решать задачи по теории вероятности

Задача 1. Классическая теория вероятности

Михаил обнаружил, что не записал последнюю цифру телефонного номера нового коллеги. Какова вероятность, что он наугад наберёт верный номер максимум с 3 раза?

Решение:

Существует 10 вариантов набора номера, и вероятность верного выбора составляет 1/10.

Согласно условиям задачи возможно несколько событий:

1. Верный номер набран сразу. Вероятность этого события составляет 1/10.
2. В первый раз Михаил ошибся, но во второй – набрал верный номер. Поскольку сначала ему пришлось выбирать 1 из 10 цифр, а затем 1 из 9, то вероятность наступления указанного события равна: P = 9/10 x 1/9 = 1/10.
3. В первый и во второй раз Михаил ошибся, а в третий – угадал верный номер. По аналогии с п. 2 вероятность этого события равна: P = 9/10 x 8/9 x 1/8=1/10.
4. С учётом 3 возможных вариантов вероятность того, что Михаил дозвониться коллеге максимум с третьего раза, равна: P = 1/10 + 1/10 + 1/10 = 3/10 = 0,3.

Ответ: 0,3.

Задача 2. Алгебра событий (умножение)

В первой корзине находятся 5 белых и 5 чёрных шаров, а во второй – 2 белых и 8 чёрных. Из каждой корзины взяли по 1 шару. Найдите вероятность, при которой оба предмета окажутся белыми.

Решение:

Пусть событие A равнозначно тому, что из обеих корзин вынули белые шары.

Также введём вспомогательные события:

E₁ – из первой корзины взяли белый шар;

E₂ – из второй корзины взяли белый шар.

Найдём вероятности наступления событий E₁ и E₂, используя классическую формулу:

P(E1) = 5/(5+5) = 5/10 = 1/2;

P(E2) = 2/(2+8) = 2/10 = 1/5.

Найдём вероятность события A:

P(A) = P(E1xE2) = P(E1) x P(E2) = 1/2 x 1/5 = 1/10 = 0,1.

Ответ: 0,1.

FAQ

В чём заключается суть теории вероятности?

Теория вероятностей (тервер) – это раздел математики, посвящённый изучению случайных событий и их свойств. Имея статистические сведения и умея находить между ними закономерности, можно прогнозировать наступление различных событий.

Какова польза теории вероятностей?

Поскольку случайность существует повсюду, теория вероятностей позволяет анализировать случайные события или результаты, строить прогнозы и использовать их в управлении процессами принятия решений. Расчёты вероятностей необходимы в разных сферах, например, в финансовой, социальной, научной.

В чём измеряется вероятность?

Как правило, вероятность выражается в виде десятичной дроби (или в процентах). Она принимает значения от 0 до 1 (или от 0% до 100%), где 0 обозначает невозможное событие, а 1 (или 100%) – неизбежное.

Как связаны теория вероятности и математическая статистика?

Эти области тесно вязаны между собой. Теория вероятностей позволяет оценивать возможность наступления случайных событий, а математическая статистика – анализировать и интерпретировать наборы сведений.

Вывод

Азы теории вероятностей и математической статистики школьники начинают осваивать в 7 классе. Этот раздел математики, на первый взгляд кажется сложным. Но чтобы понять его суть, ученику следует изучить лишь несколько базовых понятий: событие (и его разновидности), основные алгебраические операции (сложение и умножение), классическое определение (формулу) вероятности.