Теорема Виета для квадратного уравнения

Рабочая программа по Алгебре за 8 класс включает изучение теоремы Виета. Это понятие связывает корни многочлена с его коэффициентами. Данная теорема применяется в разных науках – математике, физике, экономике, везде, где требуется производить вычисления корней квадратных уравнений. В повседневной жизни формулы используются при расчете площадей, для определения прибыли от продукта или для расчета скорости объекта.

Мы доступно объясним, что такое теорема Виета для сведенного квадратного уравнения, расскажем про обратную теорему Виета. Приведем примеры, задачи и решения.

Основные понятия

Теорема – это утверждение, у которого ранее было сформулировано доказательство.

Теорема Виета – это классическое утверждение, связывающее корни многочлена и его коэффициенты. Сформулирована французским математиком Франсуа Виета в 16 веке.

Квадратное уравнение — это уравнение в виде:

аx² + bx + c = 0.

Где:

• a — первый коэффициент, не равный нулю;
• b — второй коэффициент;
• c — свободный член.

Квадратное уравнение может иметь один корень, два различных корня или не иметь корней.

Приведенное квадратное уравнение – это уравнение, в котором первый коэффициент равен 1.

Дискриминант (D) – это все корни многочлена.

Порядок вычисления дискриминанта:

D = b² − 4ac.

Как рассчитываются корни:

• D = 0, есть один корень;
• D > 0, есть два различных корня;
• D < 0, корней нет.

В случае, когда второй коэффициент четный, можно воспользоваться формулой нахождения дискриминанта:

D₁=k²−ac.

Где k=b/2.

Корень уравнения – это число, при подстановке которого в уравнение вместо неизвестного, получается верное числовое равенство.

Корни вычисляются по формулам:

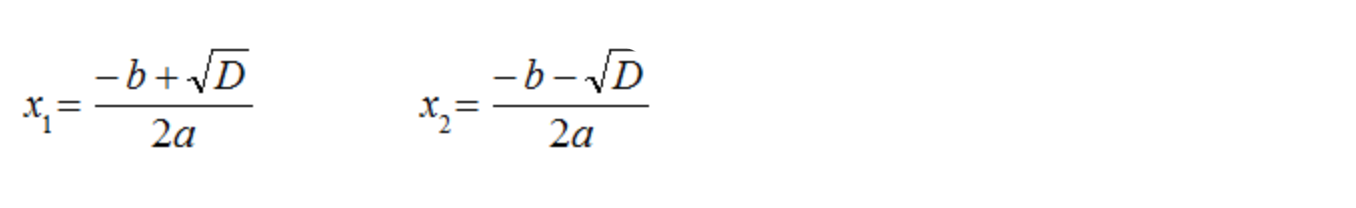
Формула Виета

Формула Виета выглядит так:

а𝑥² + b𝑥 + c=0,𝑥1⋅𝑥2 =c;𝑥1 +𝑥2 = −b

где a, b и c являются действительными числами, а x – неизвестная величина.

Теорема Виета

Формулировка теоремы Виета:

Сумма корней многочлена равна отрицательному коэффициенту при старшей степени этого многочлена, взятому с обратным знаком, а произведение корней равно коэффициенту при свободном члене.

Доказательство теоремы

Ниже приведено доказательство теоремы Виета.

Дано:

Квадратное уравнение: x² + bx + c = 0.

D > 0

Доказать:

Уравнение имеет два корня, их сумма равна второму коэффициенту с противоположным знаком, а произведение корней равно свободному члену:

x₁ + x₂ = −b,

x₁ * x₂ = c.

Доказательство будет состоять из двух частей, отдельно для каждого уравнения.

Доказательство, что x₁ + x₂ = −b:

• Для нахождения суммы корней x₁ и x₂ подставим вместо них то, что соответствует им из правой части формул корней.
• В данном квадратном уравнении x² + bx + c = 0 старший коэффициент (а) равен единице. Значит после подстановки формулы дискриминанта знаменатель будет равен 2.
  
  
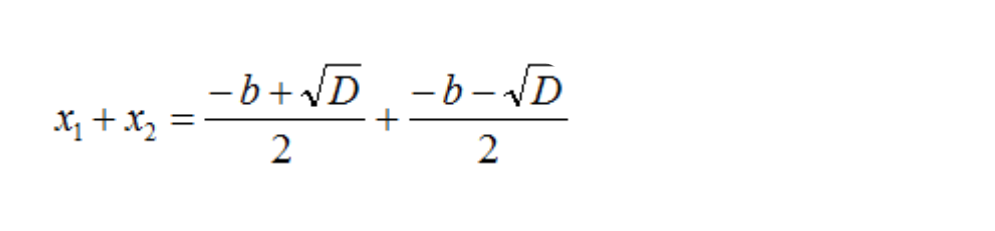
• В правой части уравнения произведем объединение числителя и знаменателя.
  
  
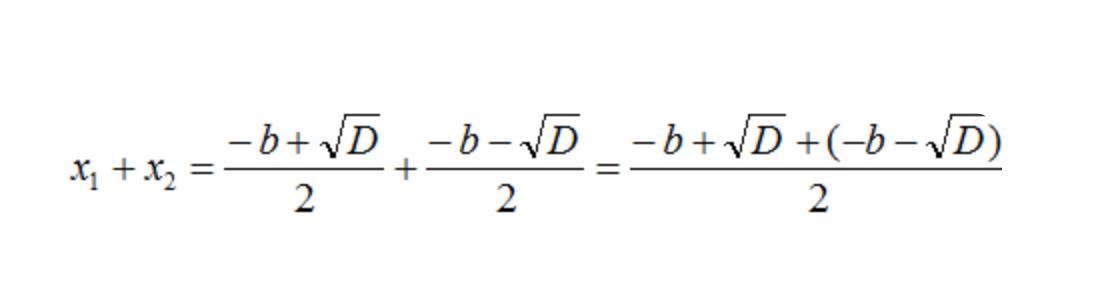
• Приведем подобные члены, раскрыв скобки и произведем сокращение:
  
  
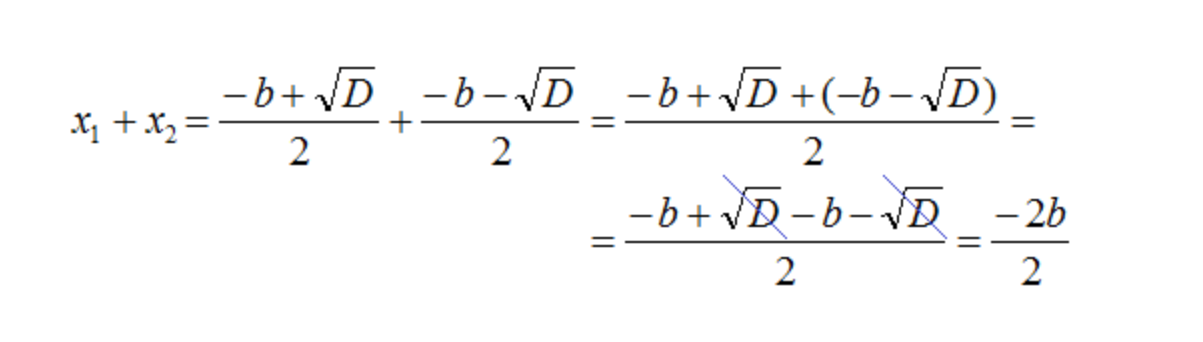
• После сокращения полученной дроби на 2, останется −b:
  
  
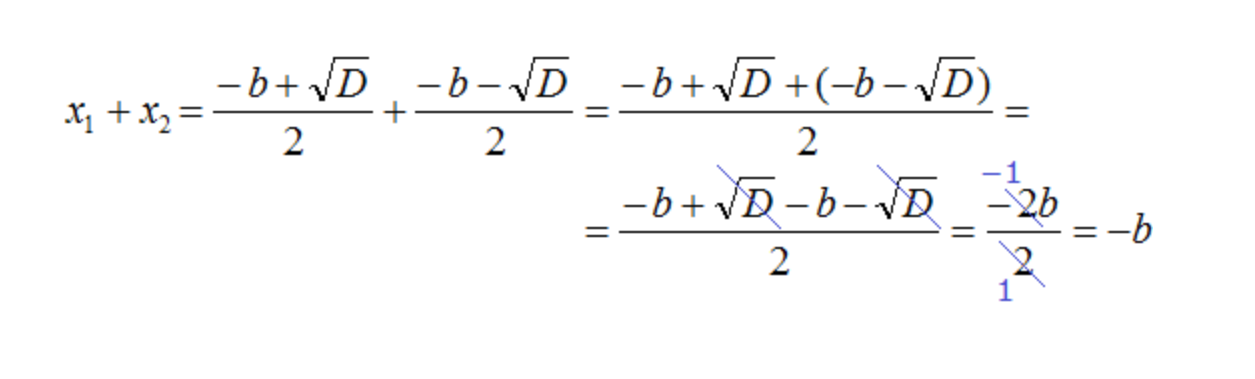
• Таким образом, мы доказали, что x₁ + x₂ = −b.

Доказательство, что x₁ * x₂ = c:

• Вместо x₁ и x₂ подставляем соответствующие части из формул корней квадратного уравнения:
  
  
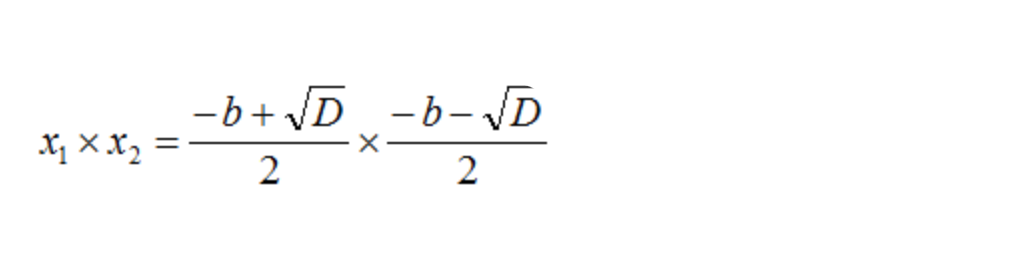
• Числители и знаменатели перемножаем между собой:
  
  
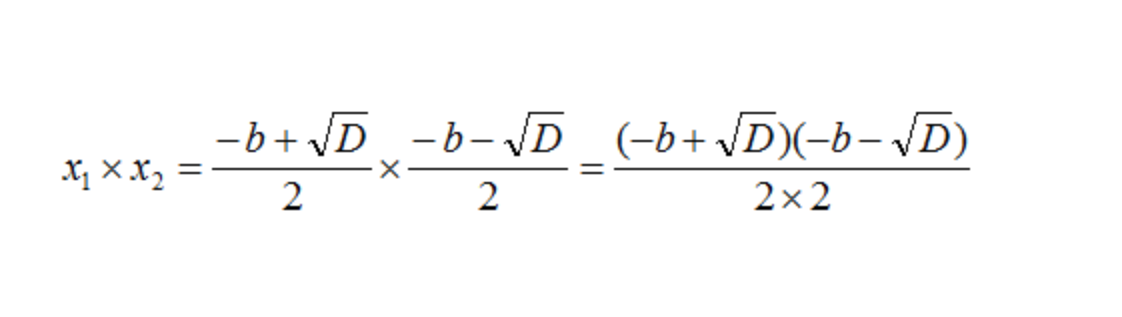
• Получилось, что числитель содержит произведение суммы и разности двух выражений. Поэтому воспользуемся формулой (a + b) * (a − b) = a2 − b2. В результате получим:
  
  
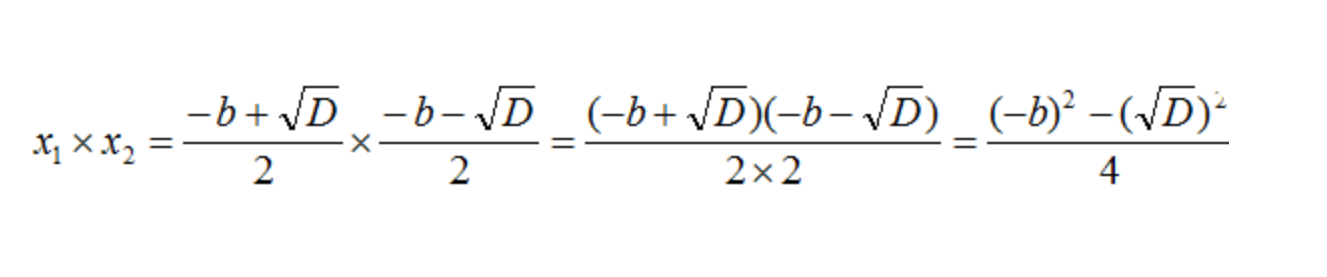
• Далее произведем трансформации в числителе:
  
  
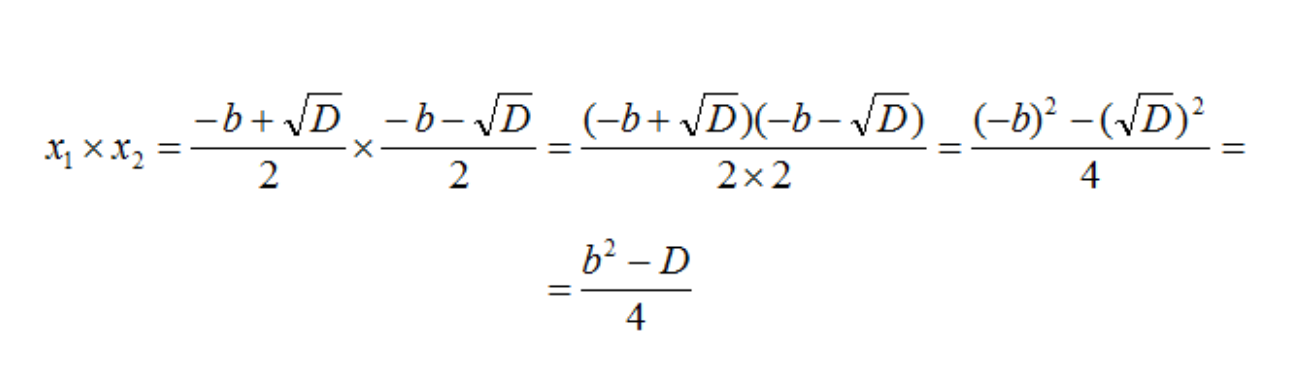
• Подставим формулу дискриминанта – D = b² − 4ac в получившееся выражение:
  
  
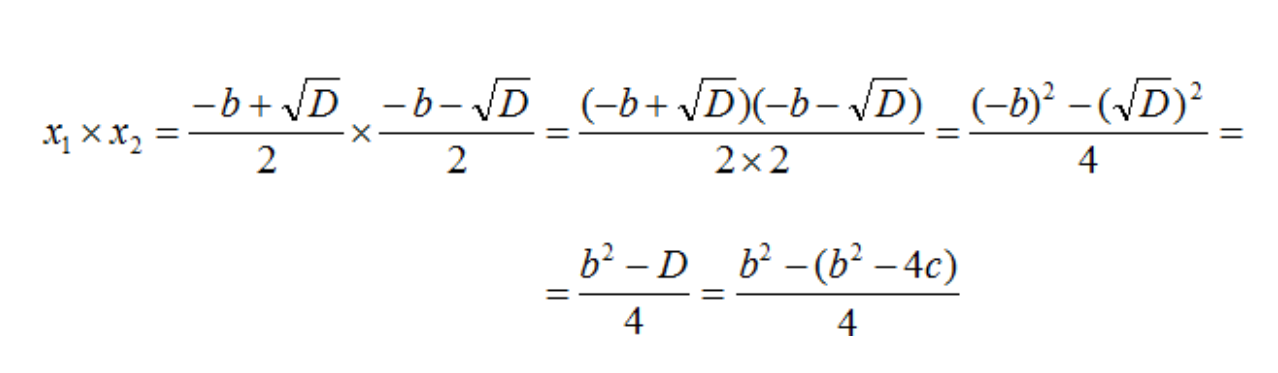
• Приведем подобные члены, раскрыв скобки и сократив:
  
  
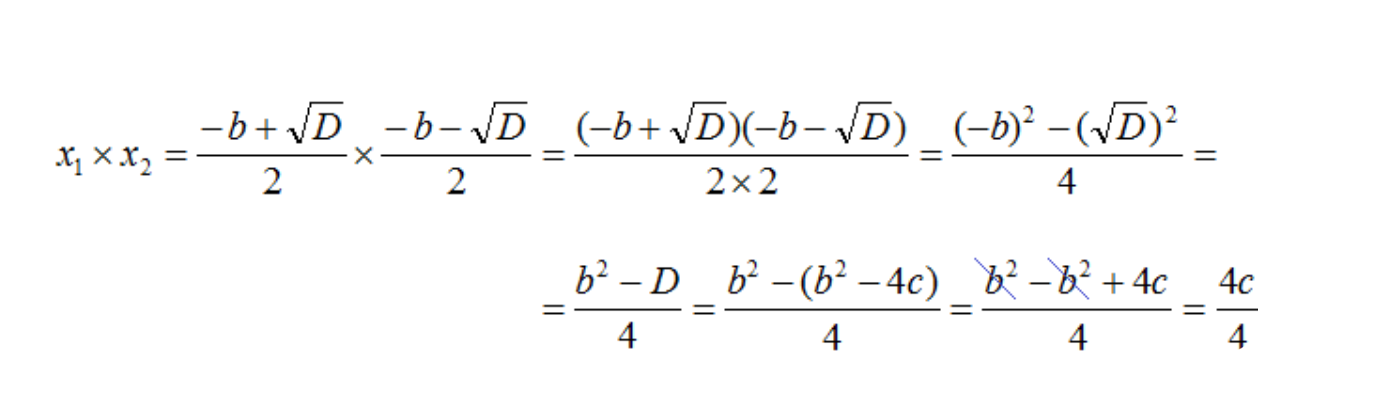
• Теперь получившееся выражение можно еще раз сократить и получить с.
• Мы доказали, что x₁ * x₂ = c.

Таким образом, теорема полностью доказана.

Примеры и задачи

Рассмотрим несколько конкретных примеров и задач с применением теоремы Виета.

Пример 1.

Рассмотрим теорему Виета на примере: x² + 4x + 3 = 0, где

• 1 – первый коэффициент;
• 4 – второй коэффициент;
• 3 – свободный член.

В соответствии с теоремой Виета сумма корней уравнения равна второму коэффициенту с противоположным знаком. Поскольку он равен 4, нужно использовать -4:

Произведение корней по теореме Виета соответствует свободному члену. У нас он равен 3. В соответствии с нашим примером получилась следующая система уравнений:

Произведем вычисление корней уравнения x² + 4x + 3 = 0.

Воспользуемся формулами для чётного второго коэффициента:

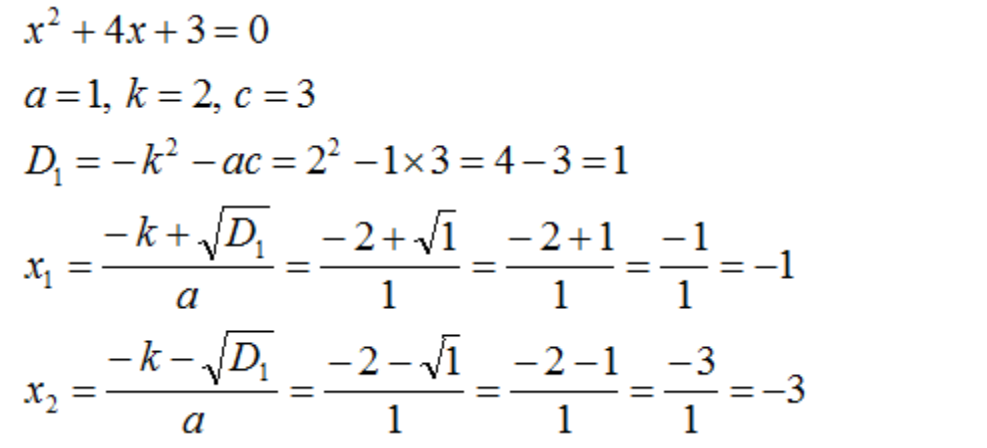
В итоге мы получили, что корнями приведенного квадратного уравнения являются числа −1 и −3.

Сумма корней равна: (-1)+(-3) = -4, с противоположным знаком получается второй коэффициент 4, т. е. решение правильное.

Произведение корней равно: (−1) х (−3) = 3, т. е. равно свободному члену, значит условие выполняется.

Таким образом, мы доказали теорему Виета на конкретном примере.

Пример 2

Дано квадратное уравнение: х²-5*х+6=0

Нужно найти корни уравнения, используя теорему Виета.

Решение:

В соответствии с теоремой Виета:

х₁+х₂=5

х₁*х₂=6

Подобрать решение просто: х₁=2, х₂=3

Ответ: х₁=2, х₂=3

Обратная теорема Виета

Обратная теорема Виета работает наоборот, и ее формулировка будет следующей:

Если некоторые два числа таковы, что их сумма равна второму коэффициенту сводного квадратного уравнения, взятому с противоположным знаком, а их произведение равно его свободному члену, то данные числа являются корнями этого сводного квадратного уравнения.

Таким образом, из соотношений x₁+x₂=−b, x₁·x₂=c следует, что x₁ и x₂ являются корнями квадратного уравнения x²+b*x+c=0.

Доказательство обратной теоремы

Докажем, что если числа x₁ и x₂ таковы, что x₁+x₂=−b, x₁·x₂=c, то сами x₁ и x₂ являются корнями приведенного квадратного уравнения: x²+b*x+c=0.

Доказательство, что х₁ является корнем уравнения в соответствии с обратным теореме Виета расчетом:

• Заменим в уравнении x²+b*x+c коэффициенты b и c на их выражения через x₁ и x₂, получим равносильное уравнение:

х²−(x₁+x₂)*x+x₁*x₂=0.

• В полученное уравнение подставляем вместо x число x₁, и получаем следующее уравнение:

х₁²−(x₁+x₂)*x₁+x₁*x₂=0.

• Данное уравнение при любых x₁ и x₂ представляет собой верное числовое равенство 0=0, х₁²−(x₁+x₂)*x₁+x₁*x₂=х₁²−х₁²−x₂*x₁+x₁*x₂=0.
• Получаем, что x₁ – корень уравнения x₂−(x₁+x₂)·x+x₁*x₂=0 или x²+b*x+c=0.
• Доказано, что, x₁ является корнем уравнения x²+b*x+c=0.

Доказательство, что х₂ является корнем уравнения:

• Подставим в уравнение х²−(x₁+x₂)*x+x₁*x₂=0 вместо х число х
• Получим уравнение: х₂²−(x₁+x₂)*x₂+x₁*x₂=0.
• Это также будет верным равенством, поскольку:

х₂²−(x₁+x₂)*x₂+x₁*x₂=х₂²−х₁*х₂−x₂² +x₁*x₂=0.

• Следовательно, x₂ тоже является корнем уравнения x₂−(x₁+x₂)·x+x₁x₂=0, а значит, и уравнения x²+b*x+c=0.
• Теорема доказана.

Пример использования обратной теоремы Виета

Дано квадратное уравнение: x² + 3x – 18 = 0

Нужно найти корни.

В соответствии с теоремой Виета:

х₁ + x₂ = – 3

х₁ × x₂ = – 18

Найдем корни посредством подбора:

х₁ = – 6

x₂ = 3

Подставляем:

– 6 × 3 = – 18

– 6 + 3 = – 3

Ответ: – 6; 3.

FAQ

Где используют обратную теорему Виета?

Обратную теорему Виета используют при подборе корней квадратного уравнения.

Пример:

Дано квадратное уравнение x2−5*x+6=0.

Чтобы числа x₁ и x₂ были корнями этого уравнения, должны выполняться два равенства:

• x₁+x₂=5
• x₁*x₂=6

Числа можно найти посредством обыкновенного подбора.

Получаем 2 и 3, так как 2+3=5 и 2*3=6.

Корнями квадратного уравнения в нашем примере являются: 2 и 3.

Также обратную теорему применяют для составления квадратных уравнений по заданным корням x₁ и x₂. Для этого нужно вычислить сумму корней, которая дает коэффициент при x с противоположным знаком приведенного квадратного уравнения, и произведение корней, которое дает свободный член.

Каким образом нужно искать корни в сложных уравнениях?

В сложных задачах решать квадратные уравнения путем обыкновенного подбора будет невозможно. Для нахождения корней применяют формулы корней квадратного уравнения через дискриминант.

Что такое формулы Виета?

Это формулы, связывающие действительные корни и коэффициенты не только квадратных, но и кубических уравнений, уравнений четверной степени, и в целом уравнений степени n.

Для получения формул Виета используют теорему о разложении многочлена на линейные множители, а также определение равных многочленов через равенство всех их соответствующих коэффициентов.

Как привести неприведенное квадратное уравнение в приведенное?

Чтобы привести неприведенное квадратное уравнение в приведенное, потребуется произвести равносильное преобразование. Нужно разделить обе части уравнения на первый коэффициент.

Знание теоремы Виета потребуется при проведении итоговой аттестации по математике?

Несмотря на то, что отдельных заданий на теорему Виета при проведении ЕГЭ не предусмотрено, знание теоремы потребуются при решении приведенных квадратных уравнений или заданий, которые сводятся к их решению.

Вывод

Формула теоремы Виета позволяет вычислить сумму и произведение корней квадратного уравнения.

Суть теоремы:

В приведенных квадратных уравнениях x² + b*x + c = 0 сумма корней равна второму коэффициенту с противоположным знаком x₁ + x₂ = −b, а произведение корней равно свободному члену x₁ * x₂= c.

Если у вас вызывает трудности решение задач с применением теоремы, попробуйте найти подобные примеры на тематических сайтах, онлайн, и подставьте свои исходные данные в уравнение.