Теорема синусов

Тригонометрия базируется на нескольких функциях, одной из которых выступает синус. Одной из сфер его практического использования выступает теорема синусов, которая устанавливает зависимость между двумя параметрами треугольника (длинами сторон и величиной углов, расположенных напротив). Тема заслуживает внимания, так как знание теоремы становится важным условием получения хорошей оценки по геометрии и успешной сдачи ЕГЭ по математике.

Теорема синусов и ее доказательство

Содержание рассматриваемой теоремы выглядит следующим образом. Стороны треугольника пропорциональны синусам противолежащих им углов. Ниже представлен внешний вид фигуры с обозначениями, которые используются для записи изложенной выше теоремы обычной математической формулой.

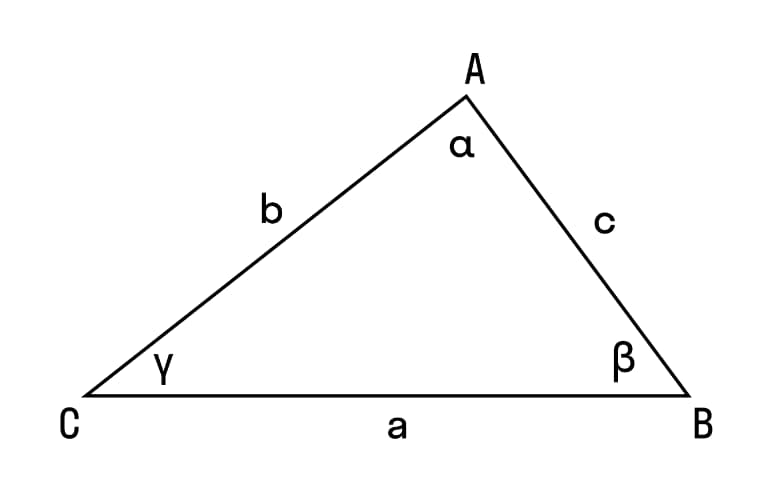
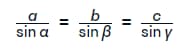
Указанный выше вариант является обычной теоремой. Что объясняется наличием еще и расширенной. Которая используется применительно к произвольным треугольникам и выглядит следующим образом:

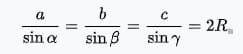
В качестве дополнительного обозначения используется R, то есть радиус окружности, которая описана около треугольника.

Чтобы доказать обычную теорему синусов, используется стандартная формула расчета площади треугольника, предусматривающая задействование синуса его угла.

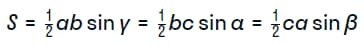
Следствием ее применения становится два соотношения следующего вида.

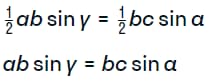
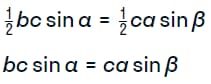
Правила позволяют сократить b, которая присутствует в обеих частях уравнений. Что дает на выходе такую картину.

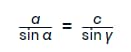
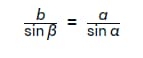
Если объединить итоговые соотношения, получаем искомое доказательство теоремы синусов.

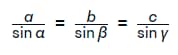
Доказательство следствия из теоремы синусов

Рассматриваемая теорема позволяет решить сразу две важных задачи. Первая – поиск сторон треугольника при условии, что известны два угла и сторона между ними. Вторая – расчет углов треугольника при наличии в качестве исходных данных двух сторон и прилежащего угла.

Не менее серьезным результатом успешного доказательства теоремы синусов становится ее расширенная версия, сформулированная выше. Ее следствием становится получение трех формул, позволяющих рассчитать радиус описанной около треугольника окружности.

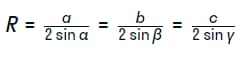
Несложные преобразования дают на выходе еще один важный результат в виде математической формулы с тригонометрической функцией. Ее смысловое содержание выглядит так: удвоенный радиус окружности, описанной вокруг треугольника, равняется отношению стороны последнего к синусу противолежащего ей угла. Сама формула имеет следующий вид:

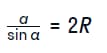
Доказательство расширенной теоремы синусов предусматривает рассмотрение трех случаев. Каждый заслуживает более детального описания.

№1. Угол А (α) треугольника ABC – острый

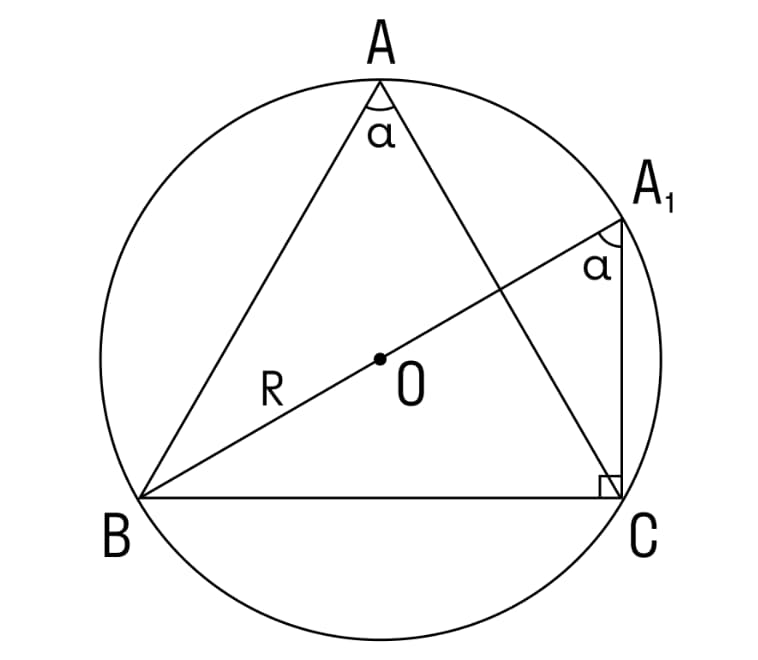
Сначала строится диаметр ВА₁. Результатом становится расположение точек А и А₁ в одной полуплоскости по отношению к прямой ВС. Исходя из теоремы вписанного угла, можно сделать вывод, что угол А будет больше угла А₁. Важно отметить, что треугольник ВА₁С является прямоугольным из-за того, что он опирается непосредственно на диаметр. Далее вычисляется катет а треугольника ВА₁С, для чего необходимо перемножить длину гипотенузы (ВА₁) на синус угла, которые расположен напротив. Решение задачи достигается выполнением трех операций:

• ВА₁ = 2R;
• а = 2R*sin α;
• R = а / (2 * sin α).

Итоговый результат является доказательством теоремы применительно к треугольнику с описанной окружностью с острым углом.

№2. Угол А (α) треугольника АВС – тупой

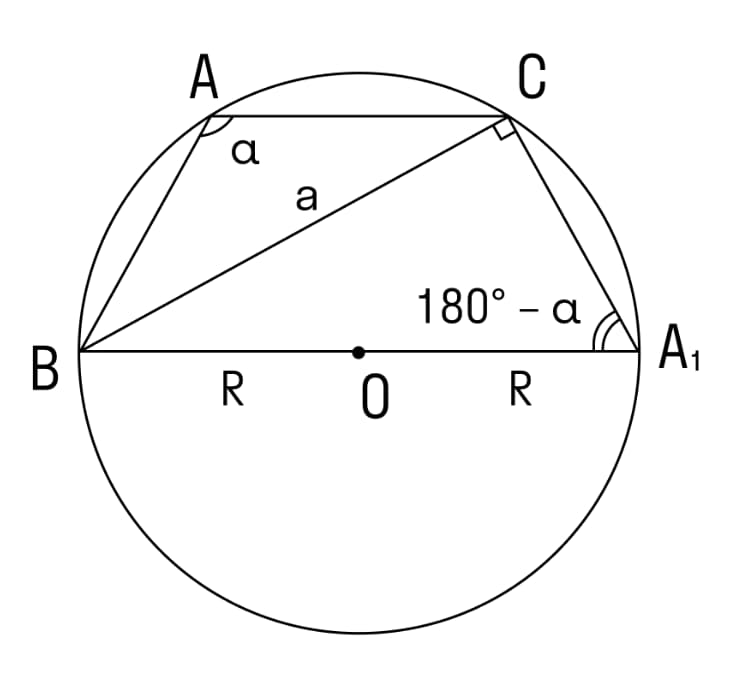
В этом случае доказательство базируется на том, что угол А1 равняется 180 градусов минус α. Данное утверждение становится следствием основного свойства вписанного в окружность четырехугольника. Далее в качестве основы для последующих выводов используются такие основания.

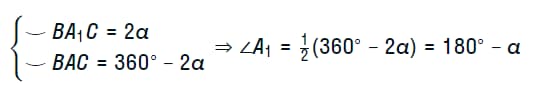
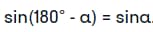
Важным дополнением становится статус прямого угла треугольника ВСА₁ у вершины С, что объясняется опорой на диаметр. Поэтому катет а рассчитывается по уже указанной выше формуле.

Отсюда следует очевидное доказательство теоремы для описанной окружности с тупым углом в виде:

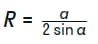
В качестве дополнения имеет смысл привести тупые углы, которые используются на практике наиболее часто. Вместе с формулами расчета синуса.

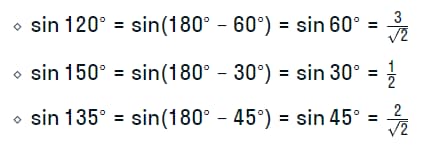
№3. Угол А (α) треугольника АВС – прямой (равен 90 градусам)

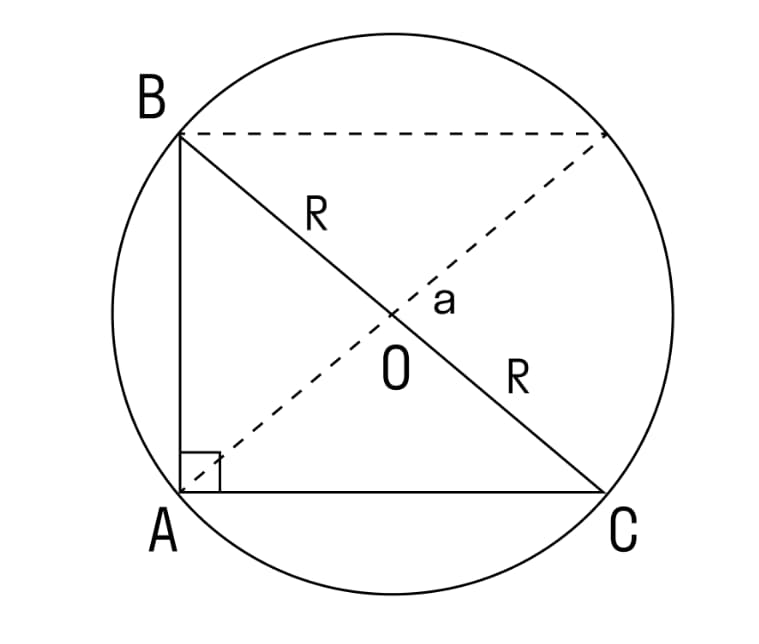
Доказательство такого варианта треугольника проще всего. Наличие прямого угла А, позволяет определить противоположную сторону как ВС = а = 2R. Следствием приведенной формулы становится вполне логичное доказательство теоремы, имеющее такую последовательность выводов:

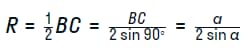
Задачи и их решения – примеры

Задачи на использование теоремы синусов появляются в 9 классе. Пример такого задания выглядит следующим образом. Нужно найти угол, расположенный напротив катета, если известна длина последнего и гипотенузы (8 и 10 см, соответственно).

Решение задачи предусматривает использование х, которым обозначается искомый угол. Соотношение сторон выражается следующим уравнением:

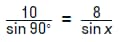
Что позволяет произвести следующие операции:

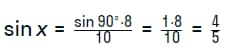
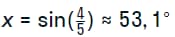
Последнее число является ответом задачи.

FAQ

В чем состоит суть теоремы синусов?

Стороны треугольника пропорциональны синусам противолежащих им углов.

Каково основное следствием обычной теоремы синусов?

Удвоенный радиус окружности, описанной вокруг треугольника, равняется отношению стороны последнего к синусу противолежащего ей угла.

В каком классе изучают данную теорему в рамках школьной программы?

В девятом.

Как найти радиус окружности, описанной около треугольника?

Значение этого параметра определяется на основании расширенной теоремы синусов (или следствия обычного варианта этой теоремы).

Вывод

1. Теорема синусов изучается в 9 класса общеобразовательной школы.
2. Суть ее предельно проста: стороны треугольника пропорциональны синусам противолежащих им углов.
3. Следствие теоремы синусов используется для определения радиуса окружности, описанной около треугольника. Его удвоенное значение равняется отношению одной из сторон фигуры к синусу противоположного угла.