Теорема Пифагора
Теорема Пифагора имеет 367 доказательств. Но в рамках школьной программы изучают значительно меньше. Рассмотрим основные формулы и доказательство теоремы Пифагора.
Теорема Пифагора – основные понятия и формула
Теорема Пифагора звучит так: «В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.» Формула при этом выглядит следующим образом:
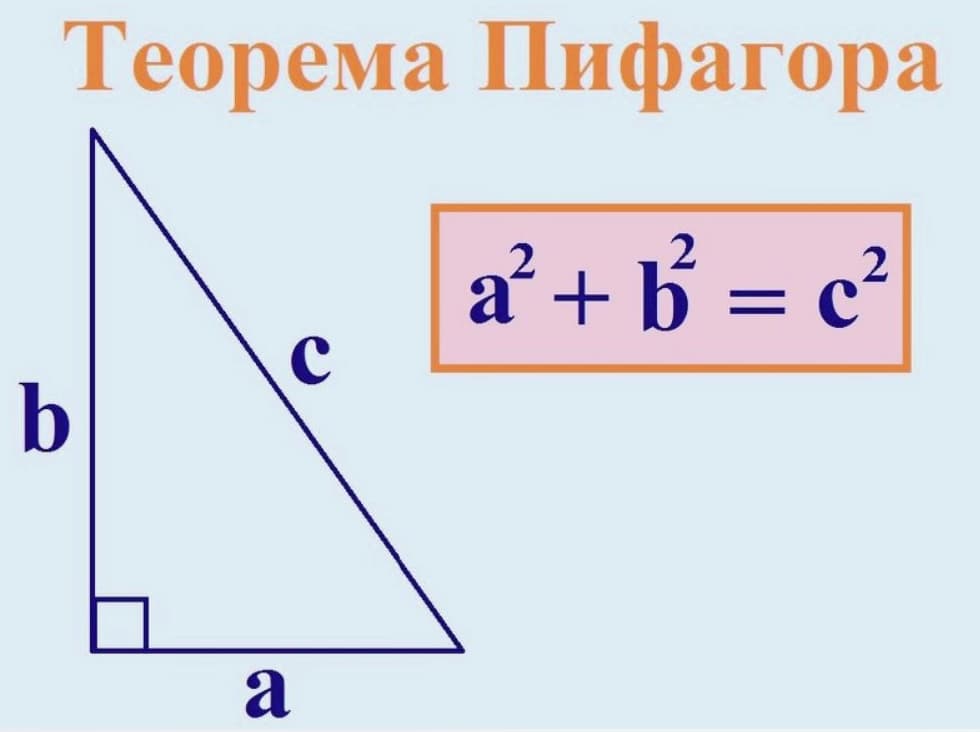
С у данного треугольника – гипотенуза, а и b – катеты.
Гипотенузой называют сторону, которая расположена напротив прямого угла. Катетом является одна из сторон, формирующих прямой угол.
Из этой формулы следует:
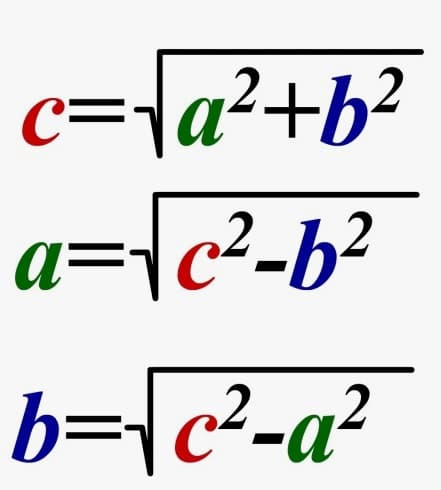

Доказательство теоремы Пифагора
В прямоугольном треугольнике гипотенуза равна сумме катетов или квадрат гипотенузы равен сумме квадратов катетов.
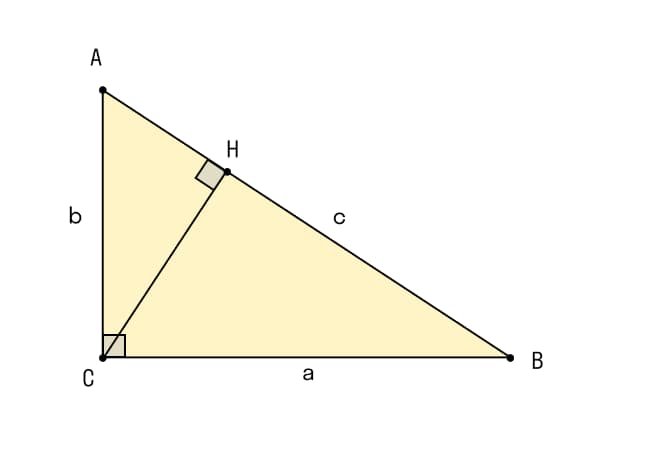
У нас есть треугольник АВС. Его угол С – прямой (∠С=900). Нам требуется доказать, что а2+b2=с2.
Доказательство выглядит следующим образом:
- Из вершины С необходимо провести высоту СН на гипотенузу АВ.
- Прямоугольные треугольники ◺АСН и ◺АВС имеют подобные углы. ∠АСВ=∠СНА=900. Угол А у них общий.
- Также подобны прямоугольные треугольники ◺СВН и ◺АВС, у которых ∠АСВ=∠СНВ=900. ∠В у них общий.
- Обозначим ВС=а, АС=b, АВ=с. Отсюда получим: а:с=НВ:а, b:с=АН: b.
- Получаем а2=с*НВ, b2=с*АН.
- Складываем равенства:
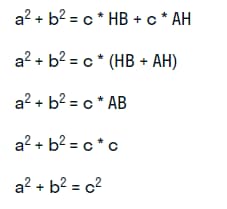
Теорема доказана.
Доказательство обратной теоремы Пифагора
Треугольник, у которого сумма квадратов 2 сторон равняется квадрату третьей стороны, является прямоугольным. Рассмотрим доказательство этой теоремы.
Имеем ◺АВС
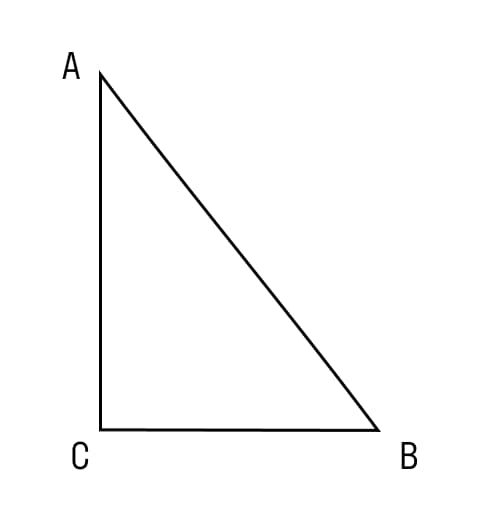
Нам необходимо доказать, что угол С прямой и равен 900.
Доказательство будет выглядеть следующим образом:
- Построим угол, равный 900. Его вершина располагается в точке С1.
- На его сторонах отметим отрезки С1А1=СА и С1В1=СВ.
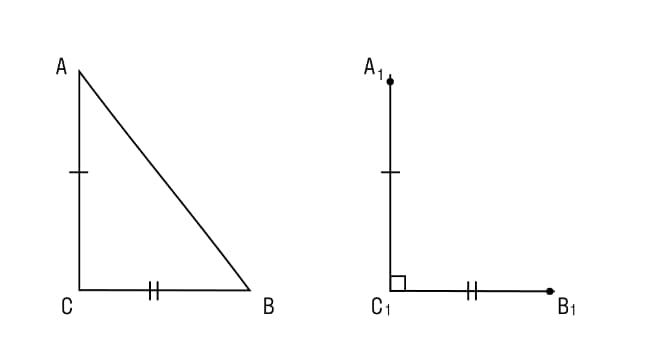
- Проведя отрезок А1В1, получим треугольник А1В1С1. У него угол С – прямой и равен 900.
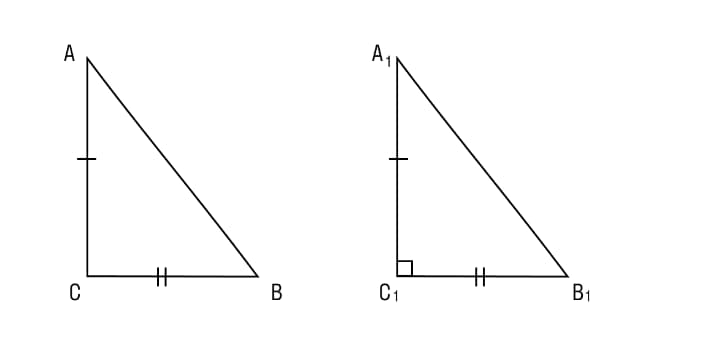
- К треугольнику А1В1С1 применим теорему Пифагора: А1В12= А1 С12+ В1С12.
- Отсюда получаем:
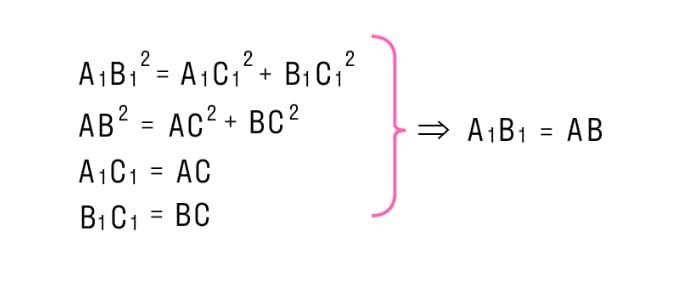
- В треугольниках АВС и А1В1С1:
СА= С1 А1 исходя из построения и АВ= А1В1 по доказанному результату. - Следовательно ◺АВС=◺ А1В1С1 по всем трем сторонам. Отсюда следует, что ∠С=∠С1=900.
А это и следовало доказать.
Разберем примеры – задачи и их решения
Рассмотрим несколько задач, решение которых основано на теореме Пифагора.


FAQ
Где можно применить теорему Пифагора?
Помимо решения задач в геометрии (определение расстояния или длин в прямоугольном треугольнике) данная теорема также используется в строительстве, физике, архитектуре, астрономии и даже литературе. Некоторых поэтов, она вдохновила на написание стихов. К примеру, немецкий писатель Адельберт фон Шамиссо написал следующий сонет:

Что такое Пифагоровы тройки?
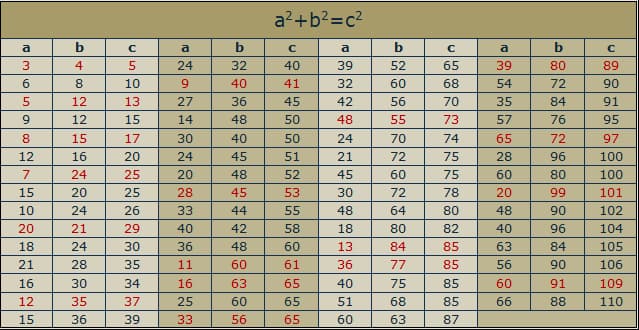
Так называют наборы из 3 чисел (а, в и с) для которых уравнение а2+в2=с2.
Вывод
Теорема Пифагора известна каждому школьнику. На ее основе строится масса других утверждений, которые помогают решать не только математические задачи, но и задания по физике, астрономии и другим наукам.
