Теорема косинусов и синусов

В 9 классе геометрия насыщена новыми материалами. Они используются на протяжении всей старшей школы, задачи, связанные с теоремами синусов и косинусов, попадают в ОГЭ и ЕГЭ. Разбираемся с теоремами косинусов, синусов, рассматриваем задачи и закрепляем материалы по этой теме.

Теорема синусов – формулировка и доказательство

Теорема синусов формулируется следующим образом: стороны треугольника пропорциональны синусам противолежащих углов. Для ее доказательства нарисуем треугольник и выразим теорему через формулу:

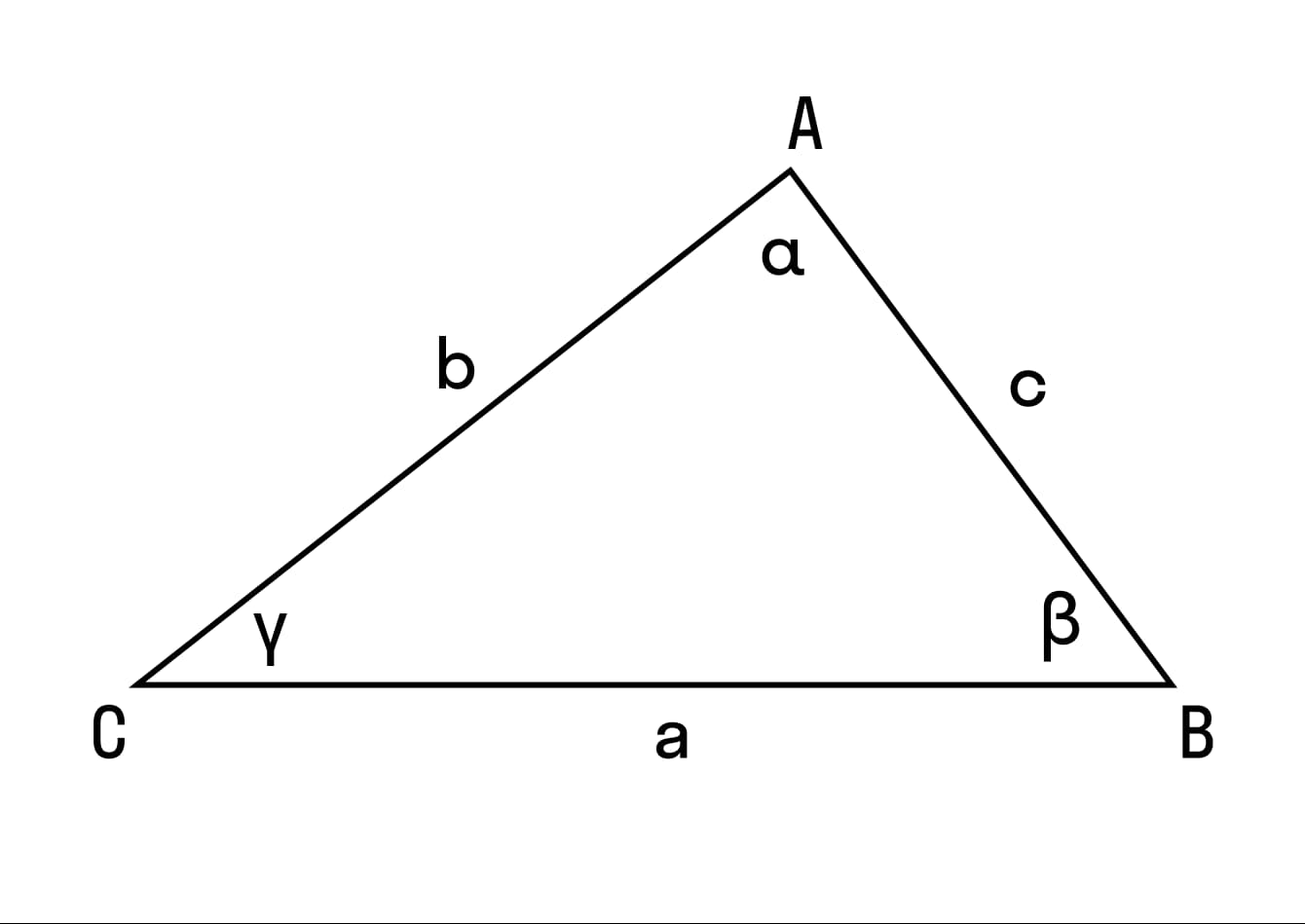
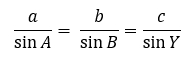
Кроме того, эти соотношения равны удвоенному радиусу описанной вокруг данного треугольника окружности. Для решения задач с теоремой синусов можно получать пропорции и находить неизвестные элементы треугольников или получать равенства с 2R и находить неизвестную величину уже таким образом.

Чтобы доказать теорему синусов, воспользуемся формулой площади треугольника через синус его угла:

Из этой формулы можно вывести 2 соотношения:

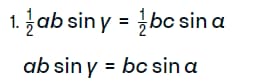
Сократим их на b с помощью правил пропорции, и мы получим равенство: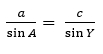 

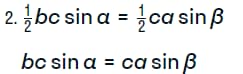
Здесь проделаем сокращение на с, что позволит нам получить: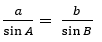 

Из этих соотношений мы установим, что:

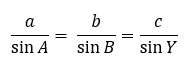
Теорема синусов доказана.

С помощью теоремы синусов находят стороны треугольника, если даны два угла и одна сторона, углы треугольника, если даны две стороны и прилежащий угол.

Следствие из теоремы синусов

Что же касается радиуса описанной около треугольника окружности, о котором было сказано ранее, нарисуем треугольник и опишем вокруг него окружность:

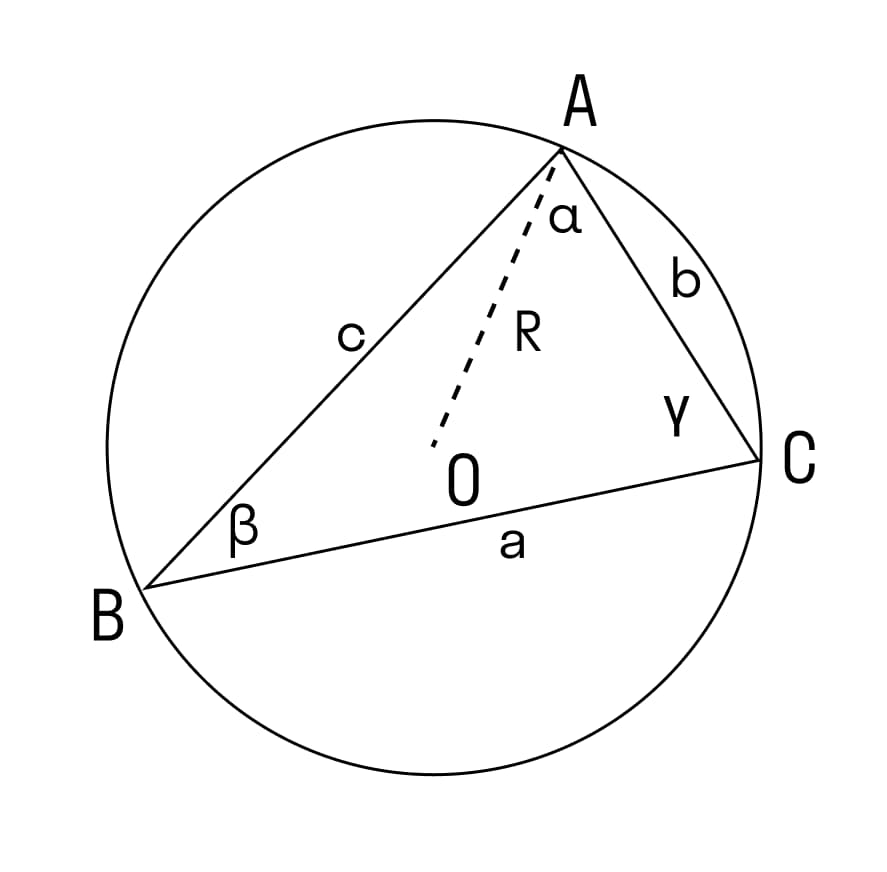
Получится такое выражение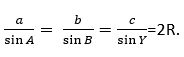 

Следовательно, можно найти радиус описанной окружности по формуле:

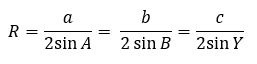
Основной смысл следствия из теоремы синусов заключается в формуле

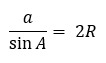
Она звучит, как: удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.

Теорема косинусов – формулировка и доказательство

Чтобы подойти к формулировке теоремы косинусов, необходимо сначала вспомнить теорему Пифагора. Она гласит, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катета. Но с помощью этой теоремы можно находить только стороны прямоугольных треугольников.

Теорема косинусов же подходит для любых. Она звучит следующим образом: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведения этих сторон на косинус угла между ними:

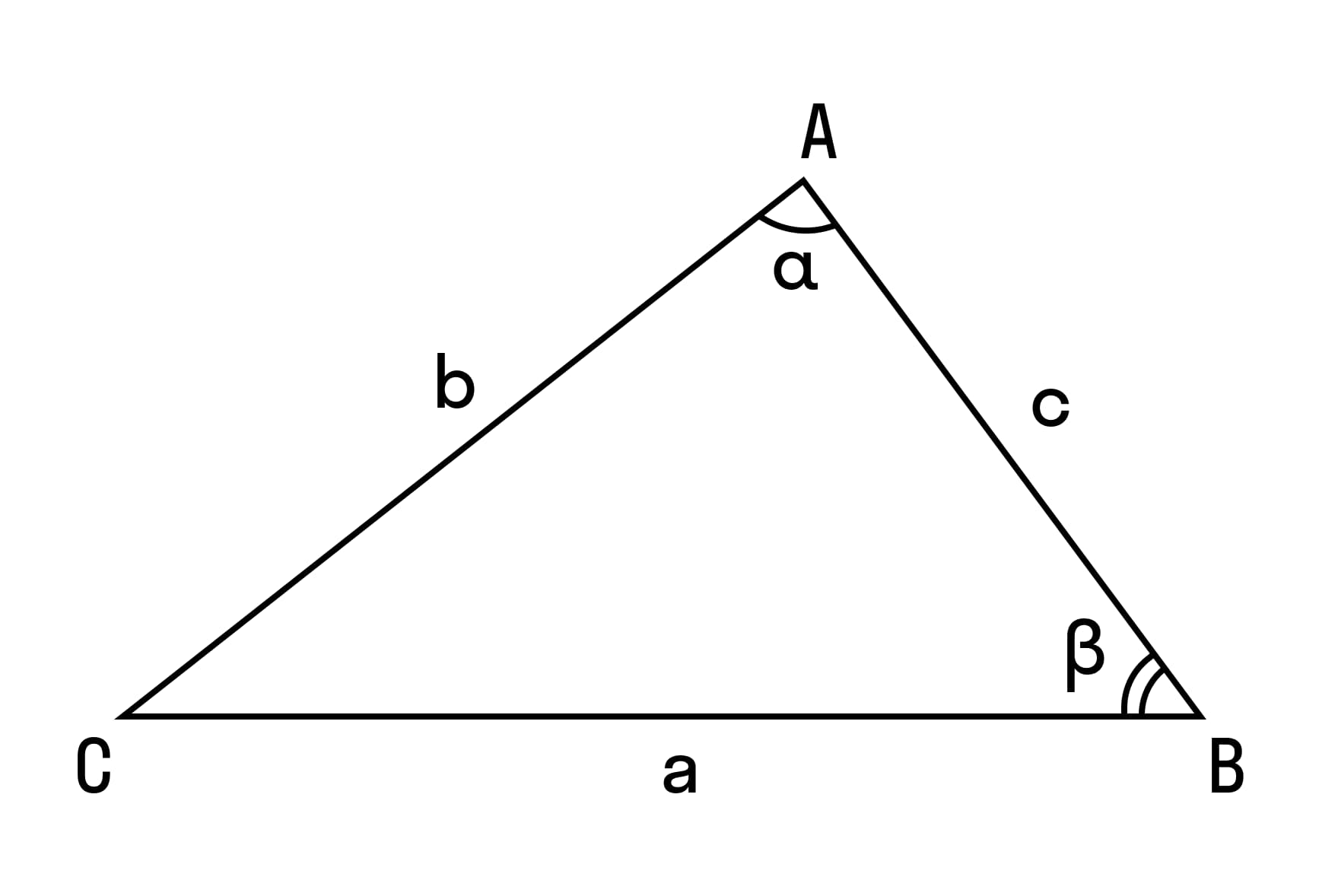
a² = b² + c² – 2bc cos a

Теорему косинусов можно доказать следующим образом:

Дан треугольник АВС, из вершины С которого на сторону АВ была опущена высота CD, значит:

• AD = b cos a,
• DB = c – b cos a.

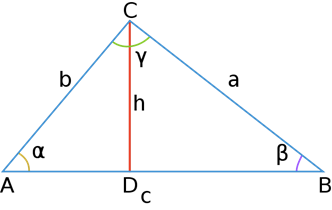
Запишем теорему Пифагора для 2-х прямоугольных треугольников: ADC и BDC:

• h² = b²- (b cos α)²
• h²= a² - (c – b cos α)²

Так как левые части у этих уравнений равны, приравниваем правые части и записываем их:

b² - (b cos α)² = a² - (c - b cos α)² или a² = b² + c² - 2bc cos α.

Теорема доказана.

Следствия из теоремы косинусов

Из доказанной формулы теоремы косинусов можно выразить косинус угла треугольника через длины его сторон, а также найти другие закономерности.

Следствие 1

Чтобы выразить cos α, треугольника со сторонами a, b, c (угол, α – противолежащий стороне а) воспользуемся теоремой косинусов:

a² = b² + c² - 2bc cos α

Перенесем cos α в левую часть уравнения и получим:

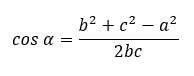
Следствие 2

Теоремой косинусов пользовались еще древние греки, но она формулировалась на языке площадей, поэтому рассматривался квадрат длины стороны треугольника, как площадь квадрата, который построен на этой стороне. Сама теорема делилась на отдельные утверждения, которые использовались для тупоугольных и остроугольных случаев значения угла α.

Поэтому теорема косинусов имеет несколько отличный вид, если вы заранее знаете, какого типа угол α перед вами. Из этого и формулируется второе следствие:

Допустим, есть треугольник со сторонами a, b, c, угол, α – противолежащий стороне а, в этом случае:

1. a²= b²+ c² (теорема Пифагора) для угла α = 90^о.
2. a²< b²+ c² для треугольников с углом α < 90^о.
3. a²> b²+ c² для треугольников с углом α > 90^о.

Докажем это следствие:

1. Так как косинус угла в 90 градусов = 0, в теореме косинусов a2= b2 + c2 - 2bc cos α часть 2bc cos α = 0, поэтому остается только a2 = b2 + c
2. cos α > 0 в тех случаях, когда угол острый, поэтому произведение 2bc cos α >0, и из теоремы косинусов получим, что a²< b²+ c², так как из правой части дополнительно отнимается определенное число.
3. cos α < 0 для тупых углов, соответственно произведение 2bc cos α будет отрицательным. Но в теореме косинусов оно вычитается из суммы квадратов сторон b и c. Поэтому a²= b²+ c²- 2bc cos α, если из него убрать какое-то число, которое добавляется к правой части станет справедливым утверждение, что a²> b² + c²

Следствие 3

Если за угол α обозначить больший угол треугольника, то с помощью следствия 2 можно определить тип треугольника: остроугольный, тупоугольный или прямоугольный. Для этого нужно просто сравнить квадрат стороны, противолежащей углу α и сумму квадратов двух других сторон:

1. a²= b²+ c² – только для прямоугольного треугольника.
2. a²< b²+ c² – только для остроугольного треугольника.
3. a²> b²+ c² – только для тупоугольного треугольника.

Разберем примеры – задачи и решение

Потренируемся в решении задач для закрепления материалов:

Задача 1:

В треугольнике ABC известно, что AB = 10, BC = 10, AC = 12. Найдите cosA.

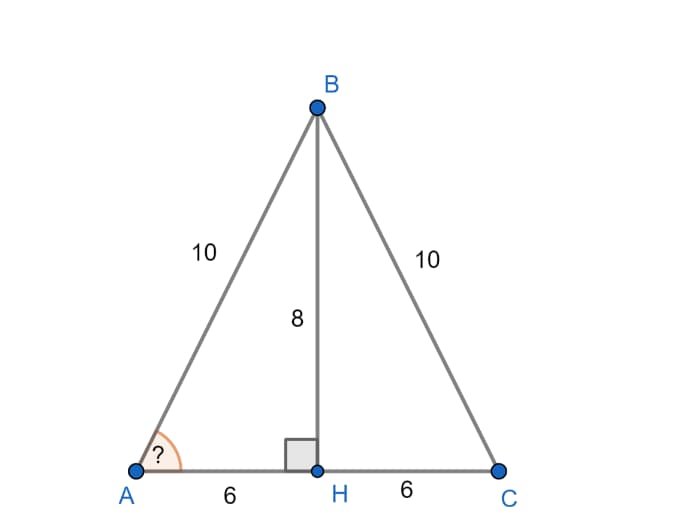
1. Так как треугольник равнобедренный, необходимо опустить высоту BH из вершины B, которая будет не только высотой, но и медианой.
2. Следовательно, AH=HC=6 (1/2AC).
3. Треугольник ABH – прямоугольный.
4. Cos угла в прямоугольном треугольнике – это отношение прилежащего катета к гипотенузе.
5. AH – прилежащий катет, AB – гипотенуза.
6. => cos A = AH/AB = 6/10 = 0,6.

Ответ: cos A = 0,6.

Задача 2:

Дано: треугольник ABC, вписанный в окружность с радиусом 3. Угол С=30^о, необходимо найти сторону AB этого треугольника.

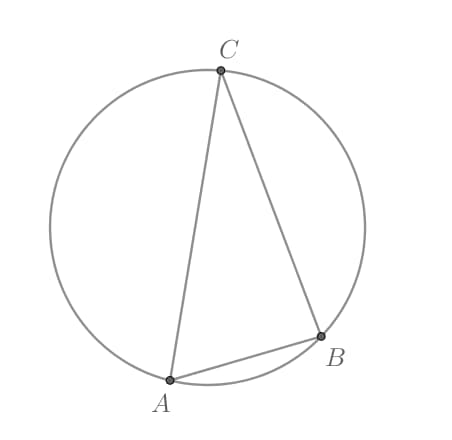
Используя теорему синусов: 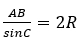 выведем сторону AB:

AB = 2R*sin C = 2*3*sin 30^o = 3

Ответ: AB = 3.

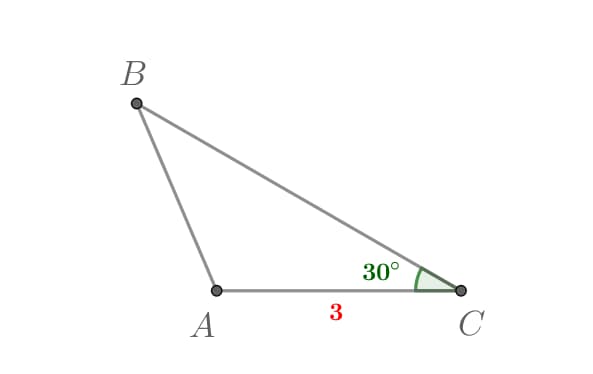
Задача 3.

Дано: треугольник ABC. Sin B = 0,6, AC = 3, угол С = 30^о. Найдите сторону АВ.

Воспользуемся теоремой синусов:

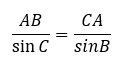
Подставим известные значения:

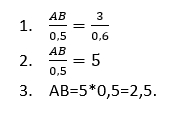
Ответ: АВ = 2,5

FAQ

В каком классе проходится теоремы синусов и косинусов?

Темы, связанные с теоремой синусов и косинусов, проходятся в 9 классе.

Как найти косинус угла в треугольнике?

Ее можно найти по теореме косинусов с использованием формулы:

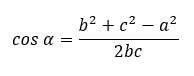
Заключение

Теоремы синуса и косинуса активно используются в решении задач в 9 классе, они встречаются и в задачах на ОГЭ, ЕГЭ. Поэтому выучить эти теоремы, разобраться в особенностях их применения – очень важно. Синусы и косинусы могут быть полезны для поиска сторон не только в прямоугольном треугольнике, но и в любом произвольном.