Таблица степеней и калькулятор
Онлайн-калькуляторы степеней – обзор
Арифметика — это простые действия с числами. Математика открывает доступ к сложным вычислениям. Например, возведение числа в степень. Сегодня в интернете можно найти калькуляторы, которые сами возводят в степень прописанные вами числа. Разработана таблица степеней, по которой можно определить каким будет число в заданной вами степени.
Однако прежде, чем проводить все эти вычисления, давайте разберемся в том, что такое степень, какие свойства имеет и попробуем решить пару задач.
Степень числа – что это, определение
Когда вы решаете математические задачи, вам предлагают одно число умножить на него же дважды, трижды или любое другое количество раз. Это действие и называется возведением числа в степень.
Например, вам нужно умножить число 2 само на себя 10 раз. Если вы не знакомы со степенями, то вы запишите пример решения следующим образом:
- 2х2х2х2х2х2х2х2х2х2. Получится 1024.
Чтобы не писать такие длинные математические примеры, было придумано записывать 2 в 10 степени или aⁿ, где:
- а — это число, которое возводится в степень. Его называют основанием степени;
- n — обозначение количества раз, на которое умножается число а. Обозначение называют показателем степени.
Прочитать записанное число в степени можно в одном из двух вариантов:
- 2 в десятой степени;
- десятая степень числа 2.
Чтобы дальше продвинуться в изучении математики, необходимо изучить степени, знать таблицу степеней и свойства. Тогда вам будет проще понимать многие действия, совершаемые в математическом анализе.
Свойства степеней
В математике существует такое понятие, как свойство степени. Каждая степень числа имеет определенные свойства и особенности. Например, если число равно 0, то 0 в пятой степени тоже будет равен 0. Эти свойства помогают решать математические задачи быстрее и с первого взгляда понимать, какие действия нужно производить над числами и степенями, чтобы получить нужный результат.
К свойствам степени относят:
- произведение степеней с одинаковым основанием. Формула этого свойства будет выглядеть так, как на рисунке ниже. Из нее следует, что прежде, чем умножать числа друг на друга, нужно сложить показатели.
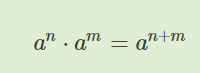
- произведение степеней с одинаковыми показателями. Формула показана на скрине ниже. Как видно из формулы, для умножения чисел с одинаковыми степенями потребуется сначала перемножить основания, а потом возвести полученное число в степень.
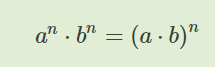
- деление степеней с одинаковым основанием. Вы можете видеть формулу на скрине. Из этой формулы следует, что нужно вычислить частное из степеней, и только потом возвести число в полученную степень.
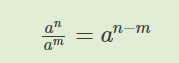
- деление степеней с одинаковыми показателями. Формула дана на скрине. При делении степеней с одинаковыми показателями, нужно пользоваться принципом умножения основания степени с одинаковыми показателями. Вначале разделить числа друг на друга, а потом уже полученный результат возвести в степень.
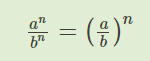
- возведение степени в степень. Формула также расположена на скрине. В нем мы видим, что при возведении степени в степень основание остается прежним, а показатели степеней перемножаются между собой. По окончании число возводится в полученный результат от перемножения степеней.
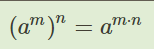
- дробная степень тоже является свойством. Вычисляется число в дробной степени по формуле, которую видно на скрине. Берется корень из основания в степени знаменателя дроби и полученный результат возводится в степень числителя дроби.
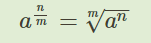
Есть еще свойства сравнения. Давайте сравним степень с нулем. Узнаем, почему «С» в степени n больше 0, при условии, что «С» больше 0.
Из вышеописанных свойств степеней мы знаем, что при умножении одного положительного числа на другое, мы получаем положительное число. Отсюда следует, что положительный результат от числа множителей не зависит, так как сам по себе результат умножения любого числа положительных чисел есть число положительное.
А степень является результатом умножения чисел. Тогда для любой степени с положительным основанием и натуральным показателем верным будет следующей выражение:
- С в степени N всегда больше 0, если само основание больше 0.
Также нам известно, что степень с основанием равным 0 всегда равна 0, в какую бы степень она не была возведена.
А теперь давайте посмотрим еще на некоторые особенности степеней:
- отрицательное число, возведенное в четную степень, – число положительное;
- отрицательное число, возведенное в нечетную степень, – число отрицательное.
Таблица степеней
Таблица возведения в степень простых чисел
|
n |
n |
n |
n |
n |
n |
n |
n |
n |
|
2 |
8 |
16 |
32 |
64 |
128 |
256 |
512 |
1024 |
|
3 |
27 |
81 |
243 |
729 |
2187 |
6561 |
19 683 |
59 049 |
|
4 |
16 |
64 |
256 |
1024 |
4096 |
16 384 |
65 536 |
262 144 |
|
5 |
25 |
125 |
625 |
3125 |
15 625 |
78 125 |
390 625 |
1 953 125 |
|
6 |
36 |
216 |
1296 |
7776 |
46 656 |
279 936 |
1 679 616 |
10 077 696 |
|
7 |
49 |
343 |
2401 |
16 807 |
117 649 |
823 543 |
5 764 801 |
40 353 607 |
|
8 |
64 |
512 |
4096 |
32 768 |
262 144 |
2 097 152 |
16 777 216 |
134 217 728 |
|
9 |
81 |
729 |
6561 |
59 049 |
531 441 |
4 782 969 |
43 046 721 |
387 420 489 |
|
10 |
100 |
1000 |
10 000 |
100 000 |
1 000 000 |
10 000 000 |
100 000 000 |
1 000 000 000 |
Задачи и решения – разберем примеры
Давайте решим тройку примеров и увидим, как работать со свойствами степеней на реальных примерах.
Пример первый.
Нужно разделить числа в двух степенях:
910 : 915
Решение задачи:
Необходимо применить свойство деления степеней с одинаковыми основаниями. В результате мы получим следующее:
910 : 95 = 910–5 =95 = 59 049
Пример второй.
Нам нужно упростить следующее выражение:
(−а8)10
Как мы будем решать эту задачу:
Здесь мы должны применить свойство возведения произведения в степень, возведения отрицательного числа в четную степень, возведения степени в степень, получим:
(−а8)10 = (−1а8)10 = (− 1)10 (а8)10 = а80.
Пример третий.
Давайте представим в виде степени следующее выражение:
(а6)b (ab)2, где b – натуральное число
Решать будем так:
Используем свойство возведения степени в степень, а затем свойство умножения степеней:
(а6)b (ab)2 = a6b a2b = a6b+2b = a8b.
FAQ
Какое выражение будет больше, если выполняется сравнение выражений с отрицательными степенями?
В этом примере больше будет то выражение, основание в котором будет меньше.
Есть ли свойства степеней с иррациональными показателями?
Да, есть. Иррациональные числа встречаются в математике с начальной школы. Есть одна особенность у степеней с иррациональными числами. Звучит она так: степень с иррациональным показателем — это степень, показатель которой бесконечная десятичная дробь или корень.
Каким будет результат, если основание равно 8, а степень у этого числа 0?
Из ранее приведенных формул, мы знаем, что любое число со степенью 0 равно единице. Значит 8 в нулевой степени будет равно 1.
Вывод
Теперь вы знаете, что такое степени и познакомились с их свойствами. Эта теория и практические примеры пригодятся вам при сдаче ОГЭ и ЕГЭ. Если вы пойдете дальше изучать математическую науку, ваши знания по степеням максимально расширятся.
