Таблица производных функций

Алгебра при переходе к каждому следующему классу школы становится все сложнее. К числу наиболее проблемных тем относятся производные функций. Дополнительные трудности в их изучении вызывает непонимание практического смысла подобных математических конструкций. Поэтому имеет смысл рассмотреть, что такое и как используются на практике производные функции.

Производная – определение и практическое применение

Начать изучение темы правильнее всего с базовых определений. Тем более – учитывая их достаточно серьезную сложность. Производной принято называть предел отношения приращения значения функции (зависимой переменной) к росту аргумента (независимой переменной) при выполнении обязательного дополнительного условия в виде стремления приращения аргумента к нулю.

Можно привести более простой и понятное определение. Производная показывает, как именно и с какой скоростью происходит изменение функции в определенной точке. Процесс расчета производной называется дифференцирование.

Для большей наглядности имеет смысл привести пример из практики. Стажер обучается на производстве. В течение первой недели скорость выполнения рабочих операций остается неизменной. Результатом чего становится график в виде константы. Производная этой функции равняется нулю, так как аргумент не меняется.

В течение второй недели скорость выполнения рабочих операций увеличивается. За аналогичное время (например, 1 минуту) стажер изготавливает не 5, а сначала 6, затем 7 и т.д. деталей. Результатом становится возрастающий график производительности. Причем производная функции будет равняться 1, что показывает скорость роста производственных показателей работника.

Важность производных в самых разных видах практической деятельности переоценить невозможно. Этот вид математических расчетов лежит в основе самых разных дифференциальных вычислений. Включая определение максимального и минимального значения функции, промежутков убывания/возрастания, скорости изменений текущего состояния объекта и многого другого. Без производной невозможно или очень трудно решать разнообразные задачи не только в теоретических аспектах математики, физики или химии, но и практических вопросах экономики, финансов, инженерии и т.д.

Производные основных функций

Количество разнообразных функций очень велико, как и их производных. Школьники изучают самые элементарные и наиболее часто встречающиеся из них, предусмотренные учебным планом и программой подготовки. Ниже приводится таблица стандартных функций и производных.

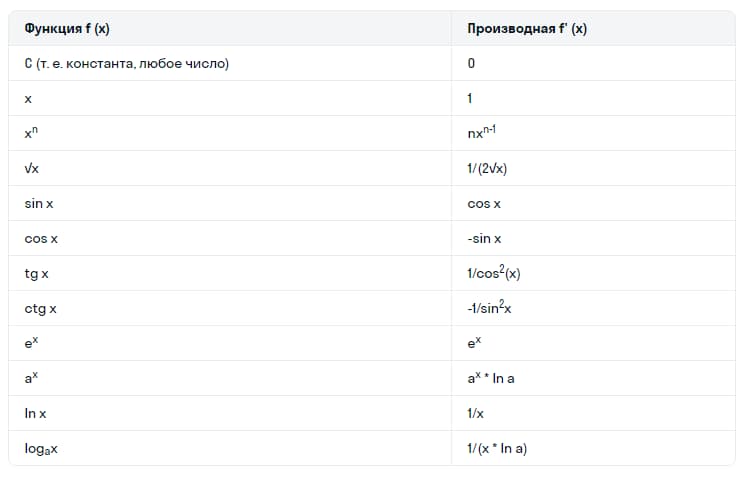
Изучение приведенной таблицы позволяет определить производную тангенса, логарифма, константы и т.д., то есть самых часто применяемых и простых функций. При этом необходимо помнить один очень существенный нюанс.

В отношении включенных в нее элементарных функций могут выполняться обычные математические действия: сложение, умножение, вычитание, деление. Осуществление подобных операций требует учета специальных правил.

Общие правила дифференцирования

Можно выделить пять базовых принципов, использование которых позволяет решить задачи на дифференцирование. Они представляют собой несложные формулы, имеющие следующий вид:

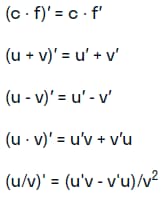
В формулах используются такие обозначения:

• с – это любой число (константа);
• f, u и v – функции.

Для упрощения формул производных функций используется стандартный принцип. Оно предусматривает внесение константы за знак производной по обычным математическим правилам.

Например, производная функции у = (6 * х³) может быть представлена в следующем виде:

у’ = 6 * (х³)’ = 6 * (x³)’ = 6 * 3 * x^3-1 = 18x².

Особенности дифференцирования сложных функций

Сложными функциями принято называть выражения, предусматривающие «вложение» одной функции в другую. Для большей наглядности имеет смысл привести пример их обозначения, который выглядит как: (f(y))’.

Дифференцирование сложной функции вполне логично требует больших усилий, чем для простых. Общим правилом становится необходимо умножения производной так называемой внешней функции на производную внутренней. Что записывается следующим образом: (f(y))’ = f’(y) * y’.

Задачи, примеры, решения

Чтобы лучше понять рассматриваемую тему, целесообразно привести несколько задач с достаточно детальным разбором решений. Сначала пример для производной элементарной функции. Задача – рассчитать производную двух следующих функций.

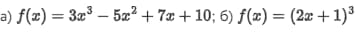
Решение задачи для первой имеет такой вид.

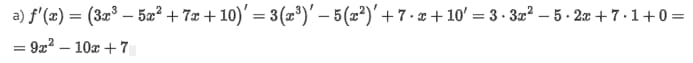
Производная второй элементарной функции определяется следующим образом.

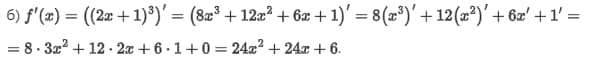
Пример задачи для сложной функции в двух вариантах:

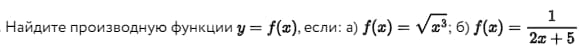
Ее решение предусматривает выполнение следующих расчетов.

FAQ

Что такое производная функции?

Если выражаться точным математическим языков, производная представляет собой предел отношения прироста значения функции к приросту аргумента (то есть зависимой и независимой переменных), причем прирост последней должен стремиться к нулю. Если говорить проще, производная показывает, как именно и как быстро меняется функция в определенной точке.

Для чего она определяется?

Определение производной принято называть дифференцированием. Его актуальность определяется очень просто: производные функций широко используются в решении множества задач, причем не только теоретических (в математике, химии или физике), но и практических (в финансах, экономике, инженерии, проектировании и т.д.)

Как узнать производную элементарной и сложной функции?

С производными элементарных функций допускается производить обычные математические действия (сложение, вычитание, умножение, деление), но с учетом пяти общих правил дифференцирования (приводятся в статье). Определение производной сложной функции требует умножения производной внешней функции на аналогичное значение внутренней.

Вывод

1. Производная – это предел отношения прироста значения функции к аналогичному изменению аргумента при условии, что последний стремится к нулю.
2. Определение производной – важная теоретическая и практическая задача, решение которой широко используется в различных науках (физика, химия, математика) и видах профессиональной деятельности (экономика, финансы, проектирование, инженерия, конструирование и т.д.)
3. Определение производных элементарных функций выполняется с применением общих правил дифференцирования. Причем они допускают проведения обычных математических действий (сложение, вычитание, умножение и деление).
4. Определение производной сложной функции требует больших усилий и предусматривает умножение производной внешней функции на производную внутренней.