Свойства умножения и деления

В 5 классе школьники начинают изучать одну из самых интересных тем в математике – деление и умножение. Уроки можно значительно упростить, если знать свойства этих действий.

В этой статье мы разберемся какие бывают свойства умножения и деления и решим примеры по каждому свойству.

Свойства умножения

Умножение – это математическая операция, которая обозначается символами «·», «×» или «*», и используется для увеличения значения одного числа на определенное количество раз.

При умножении двух чисел, первое число называется множимым, а второе - множителем. В результате операции получается произведение или результат. Количество раз, которое необходимо повторить множимое число, определяется множителем.

Например, если у нас есть число 3, и оно должно быть умножено на 4, то результатом будет 12. Это означает, что число 3 было добавлено 4 раза или воспроизведено в 4 экземплярах.

Умножение также работает с отрицательными числами. Если, например, умножить число -3 на 2, получим результат -6. Знак «-» перед числом означает, что число будет инвертировано, а затем умножено на множитель.

Также, умножение может быть представлено в виде таблицы, где каждое число представлено в строке и столбце, а пересечение строк и столбцов дает результат умножения этих чисел.

Вот пример подобной таблицы умножения:

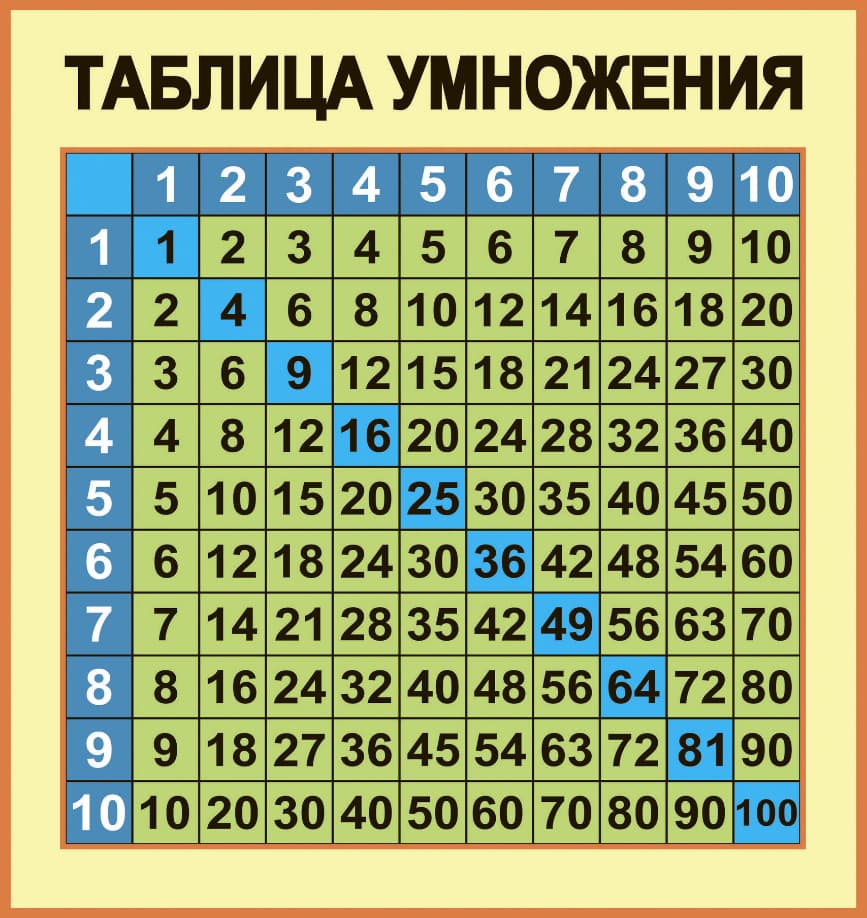
Переместительное и сочетательное свойство умножения являются одними из основных. Начнем рассматривать все свойства, начиная с этих двух.

Переместительное свойство

Переместительным свойством умножения утверждается тот факт, что порядок множителей не влияет на результат.

Другими словами, для любых чисел a и b выполняется a * b = b * a.

Например:

• 2 * 3 = 6, также как 3 * 2 = 6;
• 5 * 6 * 9 = 270, также как 9 * 6 * 5 = 270.

Важно отметить, что это свойство справедливо только для умножения, а не для всех операций.

Сочетательное свойство

Сочетательное свойство умножения означает, что результат умножения трех чисел не зависит от порядка, в котором они умножаются.

Это значит, что, для любых чисел a, b и c справедливо (a * b) * c = a * (b * c).

Например, (2 * 3) * 4 = 24, и 2 * (3 * 4) = 24.

Это свойство позволяет группировать множители в умножении, что упрощает процесс умножения.

Например, 35 * 9 * 2 = (35 * 2) * 9 = 70 * 9 = 630. Если же этот пример решать последовательно, то вычисления будут сложнее: (35 * 9) * 2 = 315 * 2 = 630.

Распределительное свойство относительно сложения

Распределительный закон умножения относительно сложения утверждает, что для любых чисел a, b и c выполняется a * (b + c) = a * b + a * c.

Например, 2 * (3 + 4) = 14, и это равносильно 2 * 3 + 2 * 4, а именно 6 + 8, что также равно 14.

То есть, умножение распространяется на каждое слагаемое внутри скобок.

Важно отметить, что это свойство работает с любым количеством слагаемых, так k * (a + b + c + d) = k * a + k * b + k * c + k * d.

Распределительное свойство относительно вычитания

В распределительных свойствах умножения относительно вычитания говорится о том, что для любых чисел необходимо умножить разность на число a * (b - c) = a * b - a * c.

Например, 2 * (4 - 3) = 2, и это равносильно 2 * 4 - 2 * 3, а именно 8 - 6, что также равно 2.

Таким образом, умножение также распространяется на каждое вычитаемое внутри скобок.

Свойство нуля

Свойство нуля гласит, что при умножении любого числа на ноль, результатом будет ноль. Другими словами, ноль является нейтральным элементом умножения.

Например:

• 3 * 0 = 0;
• 7 * 0 = 0.

Данное правило работает с любым количеством множителей: a * b * c * d * 0 = 0.

Свойство единицы при умножении

Свойство единицы утверждает, что при умножении любого числа на единицу, результатом будет это число, т.е. формула будет такой: a * 1 = a.

Например:

• 5 * 1 = 5;
• 9 * 1 = 9.

Свойства деления

Деление – это математическая операция, которая позволяет разделить одно число на другое, чтобы найти результат и остаток от такой операции. Деление обозначается символами «/» или «÷».

Деление включает в себя два основных понятия: делимое и делитель.

Делимое – это число, которое будет делиться на другое число, называемое делителем. Результат деления называется частным, а остаток – это число, оставшееся после выполнения деления.

Основная цель деления – найти число, на которое нужно разделить делимое, чтобы получить частное. В случае, если деление производится без остатка, то это называется «деление нацело». Если остаток от деления все же есть, то необходимо указать его после знака деления.

Разберем основные свойства деления натуральных чисел.

Свойство деления на самого себя

Деление на самого себя представляет простую операцию, результатом которой всегда будет единица, т.е. b / b = 1.

Например:

• 10 / 10 = 1;
• 26 / 26 = 1.

Деление на ноль

Деление на ноль – это более сложное понятие, т.к. не существует определенного значения для этой операции. Математически принято считать, что деление на число равному нулю невозможно.

Деление нуля на число

Деление нуля на число – тоже неопределенное понятие. Принято считать, что 0 / а = 0.

Например:

• 0 / 6 = 0;
• 0 / 91 = 0.

Деление на 1

Деление на 1 – это простая операция, не меняющая значение числа. Любое число, деленное на единицу, будет равно этому же числу a / 1 = a.

Например:

• 10 / 1 = 10;
• 36 / 1 = 36.

Деление суммы и разности на число

Свойство деления суммы и разности на число заключается в том, что если мы имеем сумму или разность двух чисел, то мы можем разделить это выражение на данное число: (а ± b) / c = (a / c) ± (b / c).

Например:

• (6 + 8) / 2 = (6 / 2) + (8 / 2) = 3 + 4 = 7;
• (12 – 3) / 3 = (12 / 3) – (3 / 3) = 4 – 1 = 3.

Переместительное свойство

Переместительно свойство в делении не выполняется, т.е. a / b ≠ b / a.

Например:

• 12 / 4 ≠ 4 / 12, т.к. 3 ≠ 0,3;
• 21 / 3 ≠ 3 / 21, т.к. 7 ≠ 0,4.

Свойство деления произведения на число

Свойство деления произведения на число позволяет нам разделить произведение двух чисел на данное число. Этому свойству подходят формулы:

• (a * b) / c = (a / c) * b, если a делится на c;
• (a * b) / c = a * (b / с), если b делится на c;
• (a * b) / c = a * (b / с) = (a / c) * b, если a и b делятся на c.

Например:

• (8 * 5) / 2 = (8 / 2) * 5 = 20.
• (7 * 12) / 4 = 7 * (12 / 4) = 21.
• (16 * 8) / 2 = (16 / 2) * 8 = 16 * (8 / 2) = 64,

Свойство деления числа на произведение

Свойство деления числа на произведение говорит о том, что мы можем разделить данное число на произведение двух чисел. Так получается выражение a / (b * c) = (a / b) / c = (a / c) / b.

Например, 24 / (2 * 4) = (24 / 2) / 4 = (24 / 4) / 2 = 3

FAQ

Как упростить процедуру умножения и деления чисел?

Для упрощения деления и умножения вы можете воспользоваться калькулятором. Он может быть как отдельным предметом, так и приложением в вашем телефоне или ПК.

Можно ли использовать деление и умножение с дробями или десятичными числами?

Конечно можно, на эти числа распространяются те же правила, что и на обычные.

Вывод

• Свойства деления и умножения являются основными инструментами при решении математических задач.
• Они позволяют нам упростить выражения, перемещать числа и операции в выражениях и получать правильные результаты.
• Знание и применение этих свойств помогает нам строить логические цепочки вычислений и решать сложные задачи эффективно и точно.
• Мы подробно разобрали все свойства деления и умножения, а также привели примеры решения различных задач.