Сокращенное умножение
Тему сокращенного умножения в соответствии с актуальной на сегодня школьной программе начинают изучать в 7 классе. Она представляет особый интерес для тех учеников, которые планируют в дальнейшем заниматься точными науками или поступать на инженерные и технические специальности. В статье содержится информация, которая наверняка окажется полезной как для них, так и для всех остальных школьников, так как сдавать ЕГЭ придется каждому.
Сокращенное умножение – определение и основные формулы
Формулами сокращенного умножения (часто термин дополняется еще одним словом – многочленов) называют типовые случаи умножения, которые часто встречаются на практике. Их знание и грамотное применение позволяет выполнять вычисления быстрее и проще, чем обычно.
Самые распространенные формулы приводятся в таблице ниже. Вместе с наименованием каждой, которое показывает, о каком конкретном типе умножения идет речь.
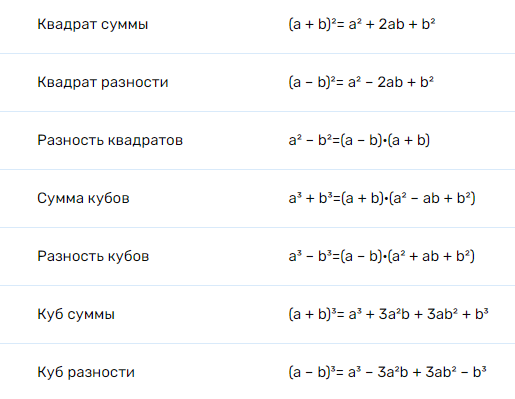
Приведенные выше формулы необходимо выучить. Доказывать их правильность не требуется. Знание правил сокращенного умножения позволяет выполнять значительную часть математических расчетов не только точно, но и максимально быстро. Первые три из приведенных выше формулы являются попросту обязательными даже для получения оценки «удовлетворительно». Остальные понадобятся для «хорошо» и «отлично», а также для высокого экзаменационного балла на ЕГЭ.
Как читать формулы сокращенного умножения?
Необходимо обязательно отметить, что вместо обозначений «а» и «b» в каждую из приведенных выше в таблице формул можно проставить не только любое число, но и переменные или даже числовые выражения. Что делает формулы по-настоящему универсальными и одновременно многофункциональными. Они могут успешно применяться практически повсеместно, а потому заслуживают еще большего внимания.
Для лучшего понимания каждой формулы следует понимать правила ее чтения. Они выглядят следующим образом (приводятся в той же последовательности, что и в размещенной выше таблице):
- Квадрат суммы равняется квадрату первого выражения в сумме с удвоенным произведением первого на второе, к которому добавляется квадрат второго.
- Квадрат разности равняется квадрату первого числа минусы умноженное на два произведение первого и второго числа, к которому добавляется квадрат второго.
- Разность квадратов двух чисел равняется произведению их суммы и их разности.
- Сумма кубов равняется произведению суммы первого и второго выражений на неполный квадрат разности между ними.
- Разность кубов равняется произведению разности первого и второго чисел на неполный квадрат их суммы.
- Куб суммы равняется кубу первого числа, к которому добавляется: умноженное на три произведение квадрата первого на второе, умноженное на три произведение первого числа на квадрат второго и куб второго.
- Куб разности равняется кубу первого числа, из которого вычитается умноженное на три произведение квадрата первого на второе число, добавляется умноженное на три произведение первого числа на квадрат второго и вычитается куб второго.
Несмотря на кажущуюся громоздкость приведенных выше расшифровок, знание формул позволяет читать их без проблем. При этом достаточно понимать значение каждого составного элемента, что избавляет от необходимости озвучивать его. Так как данное требование никак не влияет на точность и оперативность проводимых вычислений.
Нужно ли доказывать формулы сокращенного умножения?
Как было отмечено выше, рассматриваемые формулы не требуют доказательства, которым имеет смысл заниматься только в плане закрепления общих знаний по алгебре. Дело в том, что все подобные вычисления давно и успешно применяются на практике, поэтому сомнений в их точности не возникает.
Чтобы подтвердить сказанное, рассмотрим доказательство формулы разности квадратов. Она выглядит следующим образом:
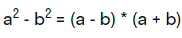
Чтобы подтвердить верность тождества, выполняются следующие действия:
- добавляем к первой части исходной формулы + a*b – a*b;
- что дает на выходе:
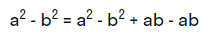
- далее производятся две перегруппировки следующего вида:
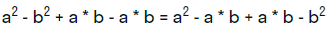
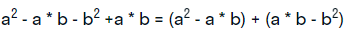
- после этого осуществляется два выноса за скобки, сначала – общих множителей:
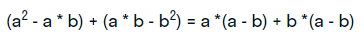
- а затем – выражения (a- b):
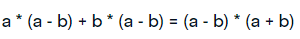
На выходе получаем вторую часть исходной формулы. Что и требовалось доказать. Во многом аналогичные действия используются для доказательства остальных формул. Поэтому приводить их в подробном формате не имеет особого смысла.
Дополнительные формулы
Помимо основных, на практике часто используются дополнительные формулы, которые также базируются на принципах сокращенного умножения. Их количество достаточно велико. Поэтому целесообразно привести в качестве примеров наиболее известные:
- Бином Ньютона.
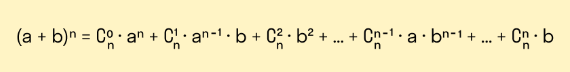
- Возведение в квадрат суммы из трех и большего числа слагаемых.
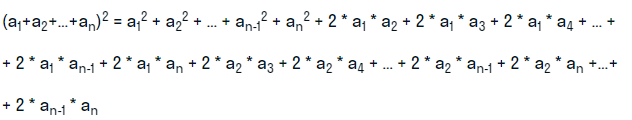
- Разность n-ых степеней двух слагаемых в трех вариантах:
- стандартном:
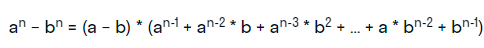
- для четных показателей:
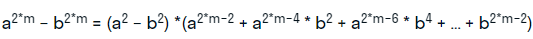
- для нечетных показателей:
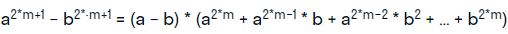
- стандартном:
Примеры и решение задач
Практическое использование формул сокращенного умножения обычно не вызывает сложностей. Намного труднее выучить их так, чтобы применять без справочных материалов. Чтобы подтвердить сказанное, рассмотрим пример обычной задачи с решением.
Задача №1. Рассчитать квадрат произведения (35 + 15)2.
Решение. Для получения ответа используется формула квадрата суммы. С ее помощью выполняются следующие действия: (35 + 15)2 = 352 + 2 * 35 * 15 +152 = 1 225 + 1 050 + 225 = 2 500.
FAQ
Что понимается под сокращенным умножением?
Это типовые случаи умножения, для которых вычисления проводятся по заранее известным и упрощенным правилам. Их использование позволяет выполнить расчет быстро и точно.
Сколько формул сокращенного умножения используется на практике?
Количество таких формул очень велико. Обязательными для школьников, желающих сдать математику на отлично, выступают семь из них.
Когда школьники начинают проходить подобные формулы?
Первое знакомство с правилами сокращенного умножения происходит в 7 классе.
Для чего необходимо изучить формулы сокращенного умножения наизусть?
С их помощью школьнику удается быстро и точно выполнять даже сложные вычисления, предусматривающие умножение переменных, чисел или даже выражений. Отсутствие знаний по теме приводит к резкому снижению оценки по предмету и результатов сдачи ЕГЭ.
Вывод
- Формулами сокращенного умножения называют типовые случаи умножения с заранее известными правилами вычислений.
- Знание и грамотное использование подобных формул позволяет произвести расчеты быстро, точно и без проблем.
- Необходимость изучения формул сокращенного умножения наизусть объясняется предельно просто: три самые распространенные из них нужны даже для получения оценки «удовлетворительно» по алгебре за 7-11 классы.
- Более высокая оценка и соответствующий экзаменационный балл на ЕГЭ требуют досконального знания всех основных формул сокращенного умножения (их количество равняется семи).
