Сокращение обыкновенных дробей

С основными свойствами дроби ученики знакомятся в 5 классе, однако работать с ними предстоит вплоть до самого окончания школьной программы. Кроме того, они могут пригодиться и в дальнейшем, в высшем или среднем профессиональном учебном заведении. Сократить дробь – значит разделить числитель и знаменатель на общий делитель – натуральное число (>0). Разберемся, для чего может потребоваться сократить дробь, почему важно это делать.

Сокращение дробей – что это

В математике очень важна точность и краткость, так как выполнять дальнейшие действия намного проще с небольшими числами, а не громоздкими. Поэтому важно сокращать все, что можно сократить. В процессе сокращения используется основное свойство дроби: при делении или умножении на одно и то же число (кроме нуля) числителя и знаменателя получится дробь, равная исходной. В виде буквенных выражений это свойство будет выглядеть следующим образом:

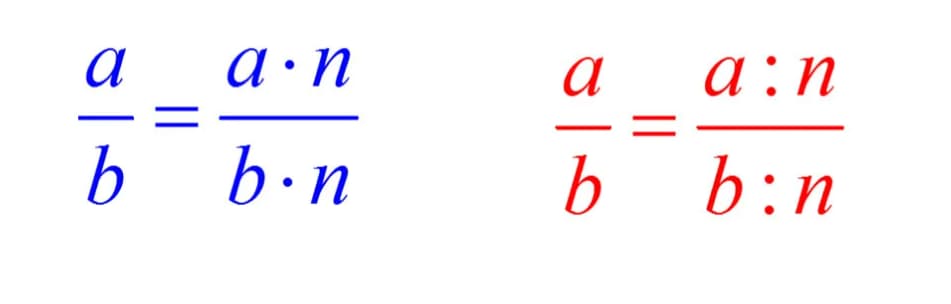
При этом a, b, n – натуральные числа.

Графически сокращение дробей выглядит следующим образом:

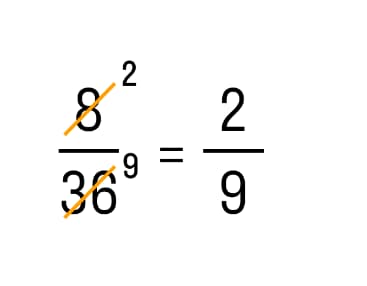
Для проведения операции сокращения числитель и знаменатель зачеркиваются, а справа над ними записывается результат их деления на общий делитель. У чисел 8 и 36 – это 4. Это число не записывается никак.

Приведение дробей к несократимому виду

Сокращение дробей проводится для того, чтобы и числитель и знаменатель состояли из наименьших возможных чисел. Например, если взять дробь: 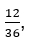 то при сокращении она примет вид  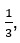так как наибольший общий делитель у этих чисел – 12. Намного проще представить и, как следствие, найти треть яблока, чем разделить его на 36 частей и выделить из них 12.

Если же в результате сокращения был выбран не наибольший общий делитель, например 6, то 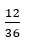 примет вид  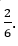Эту дробь можно еще раз сократить и привести ее к виду 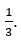. При сокращении необходимо стремится к получению дробей несократимого вида.

Для этого используется НОД (наибольший общий делитель):

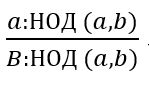 – несократимая дробь, так как свойства НОД говорят о том, что:

а : НОД(a, b) и b : НОД(a, b) являются взаимно простыми числами.

При этом два целых числа a и b могут быть взаимно простыми если их наибольший общий делитель равен единице. Примерами несократимых дробей могут быть: 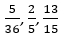 и так далее.

Правила сокращения дробей

Для того, чтобы было просто сокращать обыкновенную дробь, необходимо запомнить простой алгоритм:

1. Найти НОД числителя и знаменателя.
2. Выполнить деление числителя и знаменателя на НОД.

В 5-6 классах каждая вторая задача имеет в своих условиях или решении дроби, поэтому от умения сокращать их будет зависеть скорость и правильность решения. Самым сложным в сокращении дробей является поиск НОД. Чтобы его выполнить, необходимо уметь раскладывать числа на простые множители и хорошо помнить таблицу умножения.

Например, если дана дробь 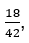 то для поиска ее НОД нужно будет разложить числитель и знаменатель на простые множители.

18 = 2 * 3 * 3

42 = 2 * 3 * 7

Из этого можно увидеть, некоторое число простых множителей совпадает. Если их перемножить, то можно получить НОД = 2 * 3. Если поделить числитель и знаменатель на 6 мы получим несократимую дробь: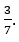 

Другой способ – просто сократить одинаковые простые множители. В итоге в числителе останется 3, а в знаменателе 7. Это позволит избежать выполнения дополнительных действий.

Разберем примеры – задачи и решение

Чтобы лучше понять материал, стоит рассмотреть несколько примеров:

Пример 1. Сократите дробь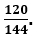 

Для этого сначала раскладываем числа на простые множители:

120 = 2 * 2 * 2 * 3 * 5

144 = 2 * 2 * 2 * 2 * 3 * 3

Из примера видно, что общими множителями являются 2 * 2 * 2 * 3. Если их убрать, то получается, что в числителе остается только 5, а в знаменателе – 2 * 3 = 6.

Поэтому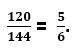  

Проверим это путем поиска НОД и деления числителя и знаменателя на него:

2 * 2 * 2 * 3 = 24.

120:24 = 5

144:24 = 6

Это действие необязательно и выполнено для наглядности.

Пример 2. Сократите дробь: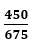 

Если в числителе и знаменателе стоят большие числа, и вы не уверены, что правильно подобрали НОД, то можно последовательно сокращать числитель и знаменатель на общий делитель.

450 = 2 * 3 * 3 * 5 * 5

675 = 3 * 3 * 3 * 5 * 5

Здесь можно зачеркнуть все одинаковые простые делители и в ответе получится 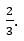 Но, так как числа большие и существует риск ошибиться в подборе делителей, можно поэтапно проверить результат.

Общими простыми делителями являются: 3 * 3 * 5 * 5. Поэтапно сократим дробь на них:

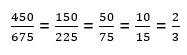
Пример 3. Сократите дробь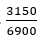 

Найдем НОД путем разложения числителя и знаменателя на простые множители:

3150 = 2 * 3 * 3 * 5 * 5 * 7

6900 = 2 * 2 * 3 * 5 * 5 * 23

При перемножении всех общих множителей между собой (2 * 3 * 5 * 5) получится, что НОД чисел 3150 и 6900 равен 150.

Разделим числитель и знаменатель на их наибольший общий делитель:

3150:150=21

6900:150=46

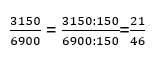
Калькуляторы для сокращения дробей – обзор

В сети существует большое количество калькуляторов, которые могут пригодиться при решении задач на сокращение дробей. Однако лучше их использовать не для того, чтобы выполнять домашние задания быстрее, а для того, чтобы лучше понять, как сокращать дроби.

Приведем примеры самых удобных, а главное – подробных калькуляторов для сокращения дробей, доступных в интернете:

• CALCULAT – простой сервис, который не только выдаст решение, но и покажет НОД. Стоит отметить, что в нем предусмотрено написание и целой части. Однако делать это вовсе необязательно, так как она останется неизменной. Кроме того, на сайте представлено несколько примеров сокращения дробей, которые позволят дополнительно закрепить материал.
• Calculator.io – здесь предложен калькулятор, который способен не просто сократить, а упростить дробь. Например, выделить целое число из неправильно дроби. Однако процесс решения этот калькулятор не показывает.
• Напишем – калькулятор, позволяющий упростить дроби, проводить вычисления, проверять полученные результаты.

FAQ

Что значит сократить дробь?

Сократить дробь – значит разделить числитель и знаменатель на общий делитель – натуральное число.

Что такое несократимый вид дроби?

Несократимая обыкновенная дробь – это когда числитель и знаменатель имеют единственный общий делитель – натуральное число, которое равно единицы. Другими словами, числитель и знаменатель – взаимно простые числа, например,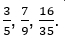 

Как проверить правильность проведенного сокращения?

Чтобы проверить, что задача решена верно, просто нужно умножить результат на НОД, на который вы делили. Должна получиться исходная дробь. Если этого не случилось, значит в расчётах была ошибка.

Заключение

Умение сокращать дроби – важный навык, который пригодиться школьнику в течение всего обучения начиная с 5 класса и заканчивая написанием экзаменов. Конечно, условно сокращать дроби не обязательно, но с помощью этой операции упрощается решение задач, не требуется работать с большими числами. К тому же, некоторые задания, особенно выполненные в электронном виде рассчитаны на получение самого простого ответа, подразумевающего проведение сокращения.