Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей изучается на уроках математики в 5 классе. Решать такие примеру достаточно просто. Все, что нужно – это выучить простое правило сложения и вычитания десятичных дробей, которое гласит «запятая под запятой». Рассмотрим тему на конкретных примерах.
Что такое десятичная дробь
Дробью в математике называют число, в котором а и b являются числами или выражениями. Следовательно дробь – это один из вариантов представления числа. Существует 2 формата записи дробей:
- обыкновенный – ½ или а/b;
- десятичный – 0,2.
Если рассматривать обыкновенную дробь, то над чертой здесь расположен числитель, а под чертой – знаменатель. Числитель является делимым, а знаменатель – делителем.
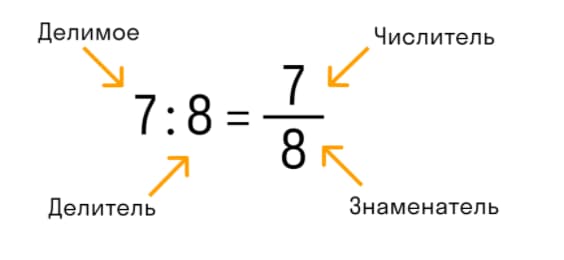
Что касается десятичной дроби, то здесь знаменатель всегда будет равен числу, кратному 10 – 10, 100, 1000. То есть десятичная дробь – это результат деления числителя на знаменатель в обычной дроби. Для отделения целой части от дробной, используют запятую: 0,3; 0,45; 5,946.
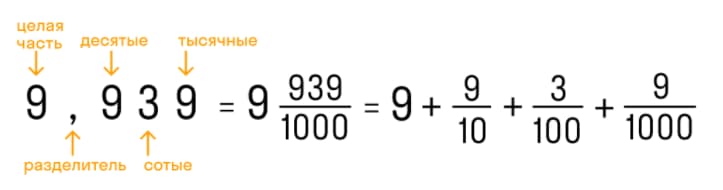
Десятичные дроби бывают:
- конечными – после запятой находится определенное количество цифр;
- бесконечными – после запятой может быть бесконечное количество цифр. Для удобства, такие дроби принято округлять, оставляя после запятой 1-3 цифры.
Свойства десятичных дробей
Основным свойством десятичной дроби является то, что приписав к ней справа любое количество нулей, ее величина останется неизменной. Если в конце дроби есть нули их можно просто упустить:
- 0,100=0,1
- 58,4500000=58,45
Между простой и десятичной дробью есть взаимосвязь:
- Целая часть смешанной и десятичной дроби равны. Если в обыкновенной дроби числитель меньше знаменателя, то его целая часть равна нулю.
- Количество цифр, которые в десятичной дроби находятся после запятой, зависит от количества нулей, которые есть в знаменатели обычной дроби.
- Дробная часть у десятичной дроби состоит из тех же цифр, что и ее числитесь в обыкновенной дроби, если ее знаменатель равен 10, 100, 1000.
Сложение десятичных дробей
Перед тем, как складывать десятичные дроби, нужно напомнить, что десятичная дробь состоит из целой и дробной частей. При их сложении каждую часть складывают по отдельности. Рассмотрим это на примере: 3,2+5,3. Сделаем это методом столбика. При этом важно, чтобы запятая стояла над запятой.


Вычитание десятичных дробей
Процесс вычитание десятичных дробей очень похож на процесс сложения. Здесь также стоит помнить о правиле «запятая над запятой», а также «одинаковое число цифр после запятой». Рассмотрим примеры вычислений.


Рассмотрим еще один пример: 7,353-3,1. Здесь после запятой разное количество цифр. Поэтому проводя вычисления к числу 3,1 необходимо дописать 2 нуля. Это нужно для того, чтобы количество цифр здесь было одинаковым. Проводим расчеты в столбик.

Еще один пример: 3-1,2. Чтобы количество цифр после запятой было одинаковым, к целому числу (3), допишем запятую и нуль.

Теперь от целой части отнимаем целую часть. При этом важно помнить, что отсюда мы уже заняли одну единицу.

Задачи для самопроверки
Рассмотрим еще несколько примеров для закрепления знаний.
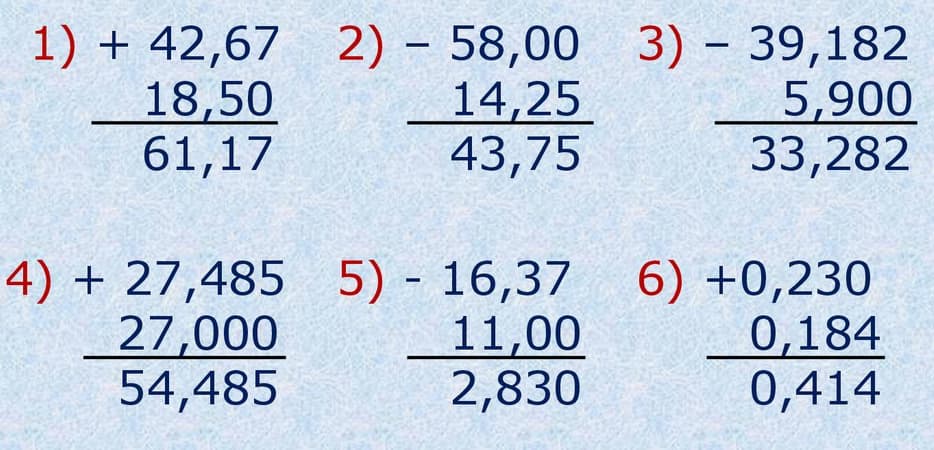
FAQ
Что такое разряд дробной части десятичной дроби?
Аналогично целому числу, дробная часть десятичной дроби может быть разбита на разряды:
- десятые – знаменатель обыкновенной дроби равен 10;
- сотые - знаменатель обыкновенной дроби равен 100;
- тысячные - знаменатель обыкновенной дроби равен 1000.
Первая цифра в десятичной дроби после запятой означает число десятых долей, вторая – число сотых долей и т. д.
Как правильно читать десятичную дробь?
Прочтение дроби зависит от количества знаков, которые стоят после запятой. К примеру, 14,3 – читается как «четырнадцать целых три десятых». 30,48 читается как «тридцать целых сорок восемь сотых».
Выводы
Правило сложения или вычитания десятичных дробей звучит следующим образом: для сложения или вычитания десятичных дробей, их записывают в столбик друг под другом, соблюдая разрядность (единицы под единицами, десятые под десятыми, запятая под запятой и т.д.). После этого обычным способом проводится сложение или вычитание.
