Скалярное произведение векторов

Скалярное произведение векторов изучают на уроках геометрии в 9 классе. Поскольку скаляр является числом, тема не самая сложная, главное в ней сразу разобраться, тогда не возникнет трудностей с решениями задач.

Мы расскажем, что такое скалярное произведение векторов, как найти произведение векторов, дадим основные определения и формулы, разберем примеры.

Произведение векторов – основные определения

Для начала дадим основные определения:

• Координаты — величины, определяющие положение точки (тела) в пространстве (на плоскости, на прямой).
• Система координат, система отсчета, используемая для определения положения точки в пространстве – это совокупность координат всех точек пространства.
• Вектор – это направленный отрезок прямой, т. е. отрезок, имеющий определенную длину и определенное направление. У вектора AB A – начало вектора, а B – конец вектора. Обозначение: .
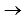• Скаляр – физическая величина, представленная числом или функцией.
  
  
• Скалярное произведение (иногда называется внутренним произведением) — результат операции над двумя векторами, являющийся скаляром, то есть числом, не зависящим от выбора системы координат.
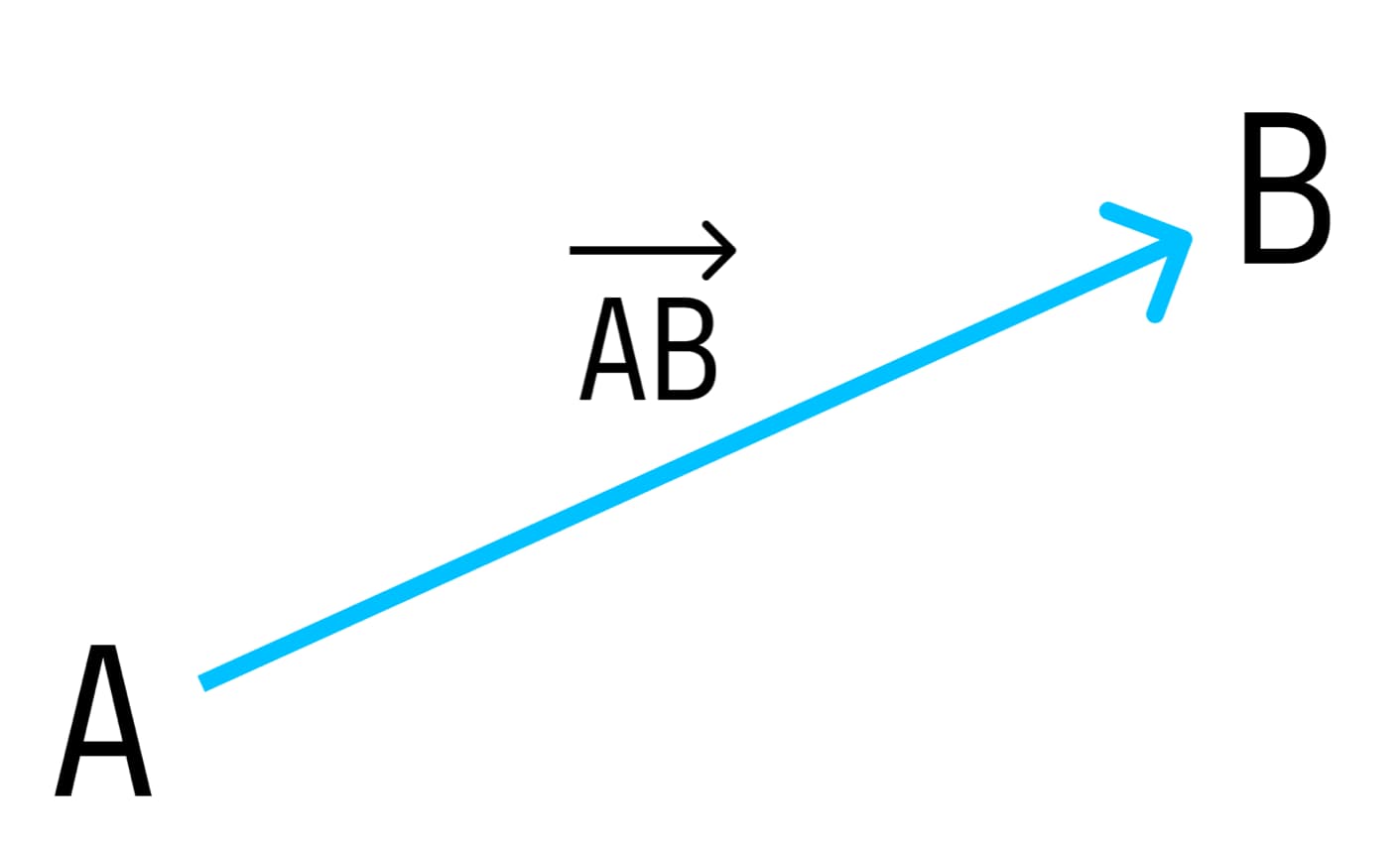
• Угол между векторами – это угол между изображающими их направленными отрезками, отложенными от одной точки пространства.

Угол между векторами

Величина угла между векторами находится в диапазоне от 0° до 180° градусов.

0°≤ ∠( aˉ; bˉ) ≤ 180° либо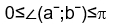 

• Если векторы перпендикулярны, то угол между ними равен 90º.
• Если векторы сонаправлены, в частности один из них или оба нулевые, то угол между ними равен 0.
• Если противоположно направленные векторы, то угол между ними равен 180º.
• Если векторы образуют тупой угол, их скалярное произведение будет отрицательным, т. к. косинус тупого угла отрицательный.

Скалярное произведение векторов

Скалярное произведение векторов — это операция в линейной алгебре, которая объединяет два вектора в скалярное значение.

Для двух векторов a = (a1, a2, ..., an) и b = (b1, b2, ..., bn), где a и b – векторы размерности n, произведением векторов будет новый вектор c = (c1, c2, ..., cn), где каждая координата ci определяется как произведение соответствующих координат исходных векторов: ci = ai * bi.

Формула для вычисления скалярного произведения векторов:
∣𝑎ˉ∣⋅∣𝑏ˉ∣⋅cos∠(𝑎ˉ;𝑏ˉ)

α – угол между векторами

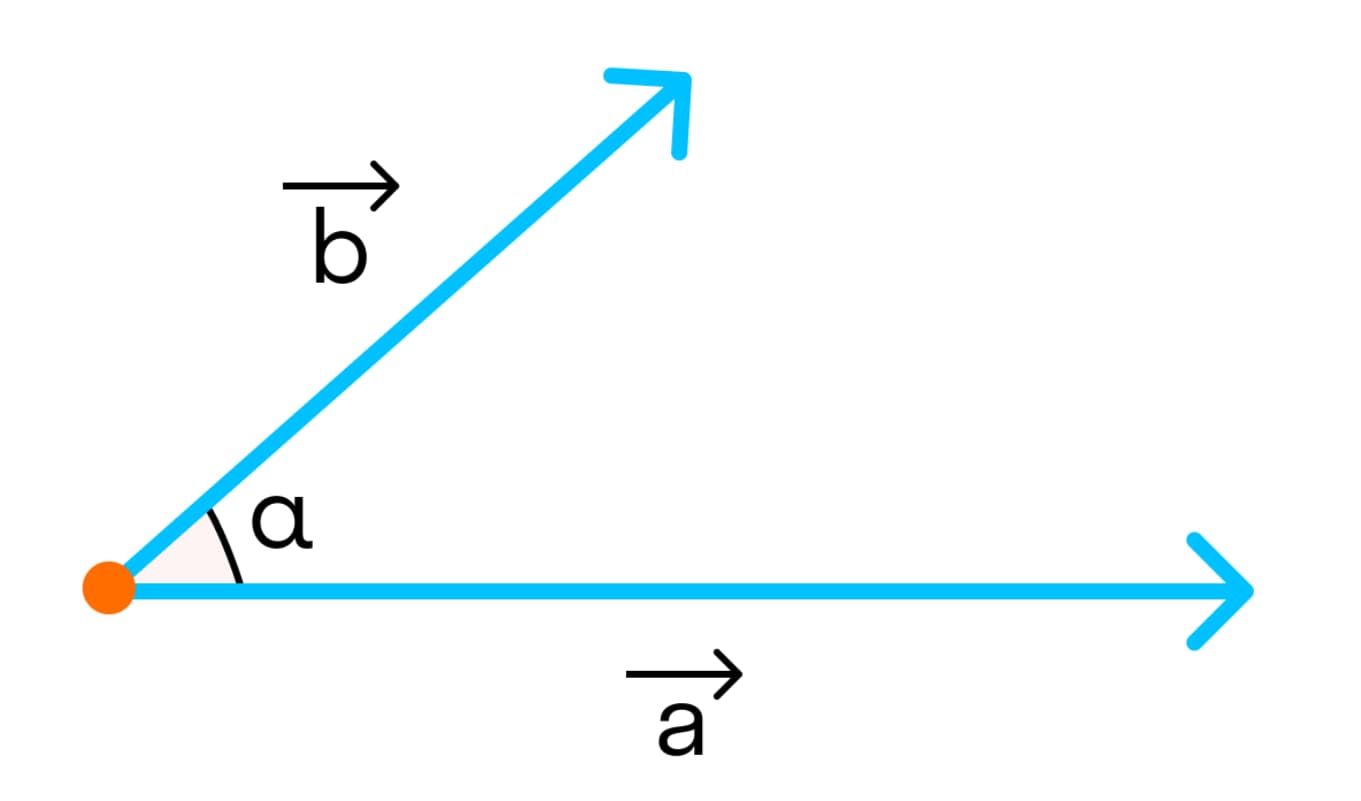
Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов, умноженная на косинус угла между ними:

• Если угол между векторами прямой, то скалярное произведение будет равным 0, так как cosα = 0.
  
  
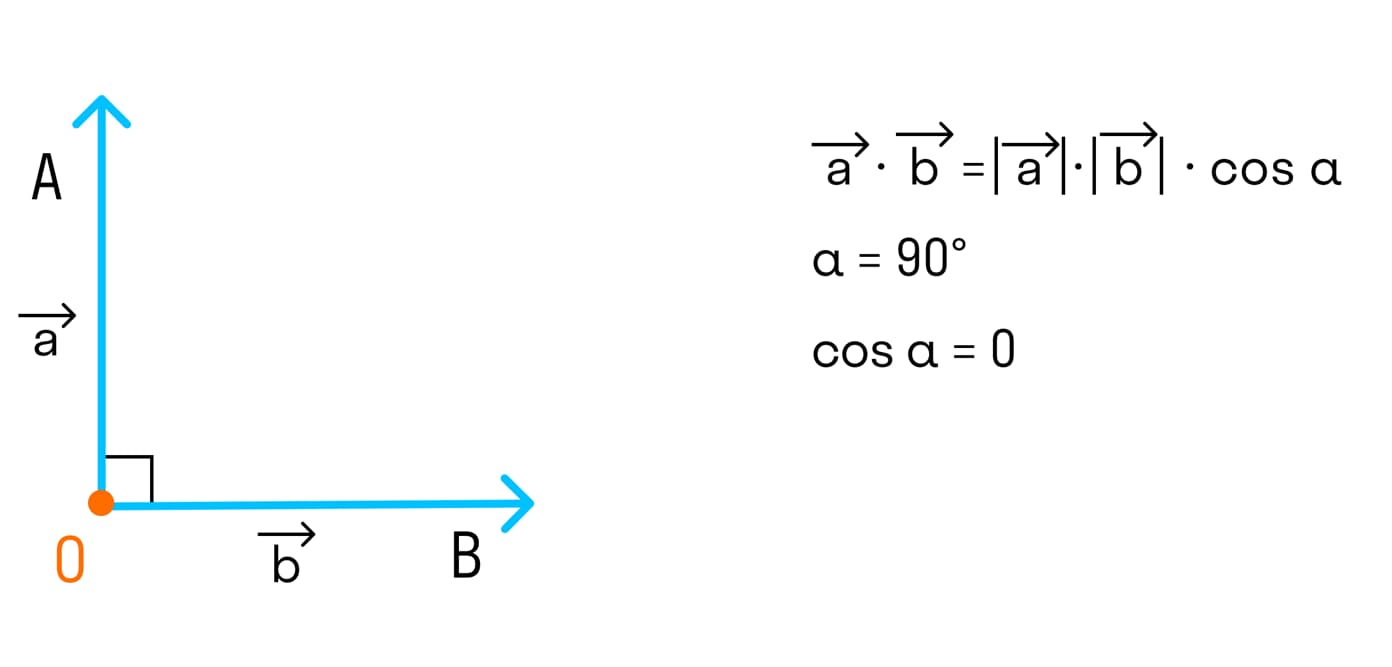
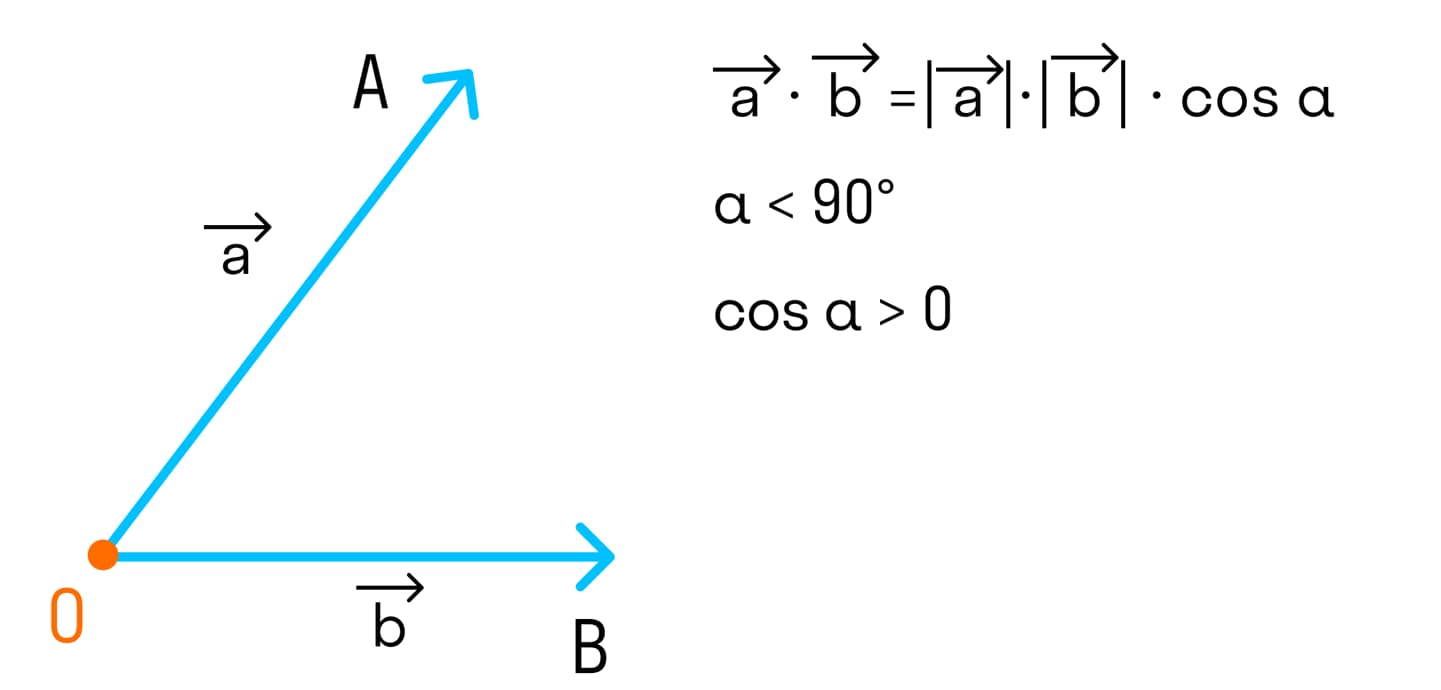
• Если угол между векторами острый и векторы ненулевые, то скалярное произведение положительно, так как cosα > 0.
  
  
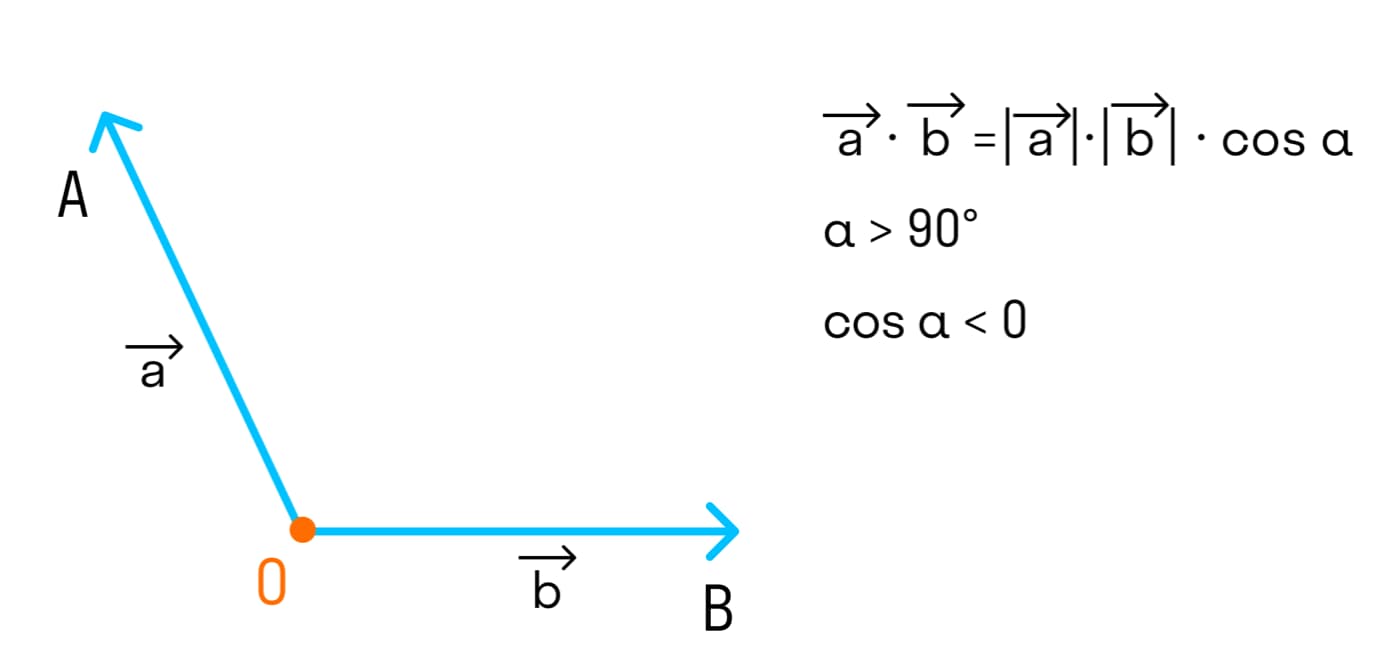
• Если угол между векторами тупой и векторы ненулевые, то скалярное произведение отрицательно, так как cosα < 0.
  
  
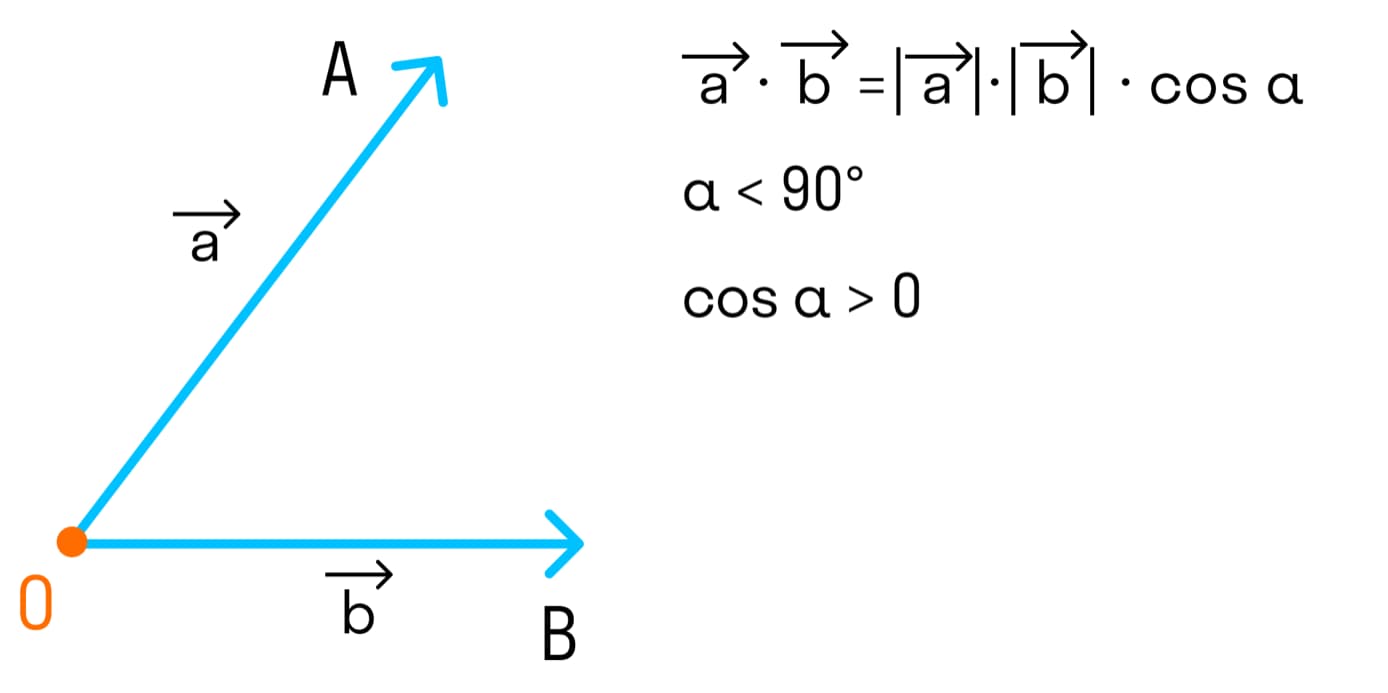
• Если угол между векторами острый и векторы ненулевые, то скалярное произведение положительно, так как cosα > 0.
  
  

Обратные утверждения будут также справедливы:

• Если 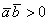, то угол между данными векторами острый. Как вариант, векторы сонаправлены.
• Если 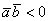, то угол между данными векторами тупой. Как вариант, векторы направлены противоположно.

Произведение векторов имеет ряд полезных особенностей. Например, если произведение векторов равно нулевому вектору, то это означает, что вектора ортогональны или линейно зависимы. Если же произведение векторов ненулевое, то векторы являются линейно независимыми.

Произведение векторов может быть использовано для нахождения угла между векторами и для определения площади параллелограмма, образованного исходными векторами. Однако, чтобы векторное произведение имело смысл, векторы должны быть трехмерными.

Скалярное произведение в координатах

Скалярное произведение двух векторов на плоскости или в трехмерном пространстве в прямоугольной системе координат – это сумма произведений соответствующих координат векторов.

Математически скалярное произведение двух векторов a и b в координатах может быть выражено следующей формулой:

a · b = a₁b₁ + a₂b₂ + ... + aₙbₙ

где a₁, a₂, ..., aₙ и b₁, b₂, ..., bₙ - координаты векторов a и b соответственно.

На плоскости в прямоугольной декартовой системе координат для векторов a = (a_x, a_y), b = (b_x, b_y) скалярное произведение вычисляют по формуле:

a_x * b_x + a_y * b_y

В трехмерном пространстве для векторов a = (a_x, a_y, а_z), b = (b_x, b_y, b_z) скалярное произведение вычисляют по формуле

 = a_x * pb_x + a_y * pb_y + а_z * pа_z

Свойства скалярного произведения векторов

В скалярных произведениях есть несколько важных свойств, пользуясь которыми можно решать различные задачи, например, находить угол между векторами или проверять их ортогональность.

Свойства:

• Коммутативность: a * b = b * a.
• Дистрибутивность относительно сложения: (a + b) * c = a · c + b * c.
• Линейность: (λa) * b = λ(a * b), где λ – скаляр.
• Скалярное произведение вектора самого на себя всегда больше или равно нулю.

Скалярное произведение вектора самого на себя будет равным нулю тогда и только тогда, когда вектор равен нулевому вектору: 𝑎⃗∗ 𝑎⃗> 0 и 0⃗∗ 0⃗ = 0.

• Скалярное произведение вектора самого на себя равно квадрату его модуля: 𝑎⃗ ∗ 𝑎⃗ = ∣𝑎⃗∣²
• Если скалярное произведение двух ненулевых векторов равно нулю, то эти векторы перпендикулярны друг другу (ортогональны): а и b ≠0, a ∗ b=0 ⟺ a ⊥ b.

Разберем примеры вычислений – задачи и решение

Примеры для плоских задач

1. Найти скалярное произведение векторов a = {1; 2} и b = {4; 8}.
   Решение: (a, b) = 1 * 4 + 2 * 8 = 4 + 16 = 20.
   Ответ: 20
2. Найти скалярное произведение двух векторов a и b, если их длины равны 3 и 7 соответственно, а угол между ними равен 60 градусам.
   Решение: Для определения скалярного произведения применим основную формулу: (𝑎⃗, 𝑏⃗) = ∣𝑎⃗∣ ∗ ∣𝑏⃗∣ ∗ cos (𝑎⃗, 𝑏⃗) = 3 ∗ 7 ∗ cos60° ∗ 1/2 = 21/2 =10,5
   Ответ: 10,5
3. Найти скалярное произведение векторов 𝑎⃗ и 𝑏⃗, если ∣𝑎⃗∣ = 2, ∣𝑏⃗∣ = 5, ∠(𝑎⃗, 𝑏⃗ = 𝜋/6).
   Решение: применим формулу (𝑎⃗ ∗ 𝑏⃗) = ∣𝑎⃗∣ ∗ ∣𝑏⃗∣ ∗ cos𝛼(a ∗ b) = 2 ∗ 5 ∗ cosπ/6 =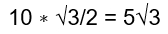 
   Значение косинуса нашли и по тригонометрической таблице.
   Ответ: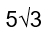 
4. Найти скалярное произведение векторов: 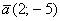 и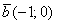 
   Решение: Применим формулу: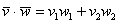 
   
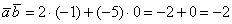
   Ответ: -2
5. Проверить ортогональность векторов: 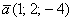 и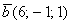 
   Решение: Вычислим их скалярное произведение: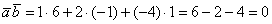 , следовательно,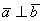 
6. При каком значении 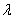 векторы  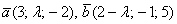будут ортогональны?
   Решение: По условию требуется найти такое значение параметра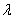 , чтобы данные векторы были ортогональны. Два вектора пространства  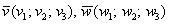ортогональны тогда и только тогда, когда .
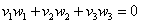   Нужно составить уравнение: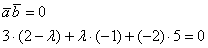
   
   Раскрываем скобки и приводим подобные слагаемые: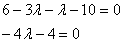
   
   
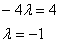
   Ответ: при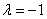 

Примеры вычисления скалярного произведения векторов для пространственных задач

1. Найти скалярное произведение векторов a = {1; 2; -5} и b = {4; 8; 1}.
   Решение: a * b = 1 * 4 + 2 * 8 + (-5) * 1 = 4 + 16 - 5 = 15.
   Ответ: 15
2. Найти скалярное произведение векторов 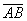 и 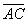, если даны точки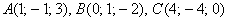 
   Решение: Найдем векторы: .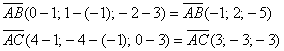
   Применим формулу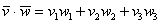  и вычислим скалярное произведение: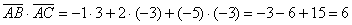 
   Ответ: 6

Пример вычисления скалярного произведения для n -мерных векторов

• Найти скалярное произведение векторов a = {1; 2; -5; 2} и b = {4; 8; 1; -2}.
  Решение: a * b = 1 * 4 + 2 * 8 + (-5) * 1 + 2 * (-2) = 4 + 16 - 5 -4 = 11.
  Ответ: 11

FAQ

Что такое алгебраическая интерпретация скалярного произведения векторов?

Алгебраическая интерпретация:

Скалярным произведением двух векторов a и b будет скалярная величина, равная сумме попарного произведения координат векторов a и b.

Что такое геометрическая интерпретация скалярного произведения векторов?

Геометрическая интерпретация скалярного произведения векторов:

Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов умноженного на косинус угла между ними.

Как обозначается и рассчитывается скалярный квадрат вектора?

Скалярным квадратом вектора называют скалярное произведение вектора a на себя, т. е. когда два вектора равны.

Он обозначается через a² и равен квадрату длины вектора a.

Что такое векторное произведение векторов?

Векторным произведением векторов является вектор, который перпендикулярен плоскости, построенной по двум сомножителям, являющимися результатом бинарной операции «векторное умножение» над векторами в трехмерном евклидовом пространстве.

Если векторы заданы в прямоугольной системе координат трехмерного пространства, векторное произведение векторов (вектор с) будет иметь следующие свойства:

• если векторы a и b коллинеарны, он будет нулевым;
• он перпендикулярен и вектору a и вектору b;
• длина векторного произведения равна произведению длин векторов a и b на синус угла между ними.

Чем отличаются скалярное и векторное произведение векторов?

• Векторное произведение не имеет свойств коммутативности и ассоциативности (антикоммутативное).
• Векторное произведение является вектором, а скалярное числом.
• В отличие от формулы для вычисления по координатам векторов скалярного произведения в трехмерной прямоугольной системе координат, формула для векторного произведения зависит от ориентации прямоугольной системы координат.
• Векторное произведение обозначается квадратными скобками.

Вывод

• Скалярное произведение векторов имеет множество приложений в различных областях, например в физике, геометрии и машинном обучении. Оно помогает определить угол между векторами, вычислить длину проекции одного вектора на другой и решить множество задач, связанных с векторами.
• Разобраться в теме помогут наши примеры и решение практических задач на эту тему.