Решение уравнений с дробями

Решение уравнений с дробями представляет собой важный аспект алгебры, который встречается в различных математических задачах и прикладных областях. Этот процесс может быть как относительно простым, так и достаточно сложным в зависимости от структуры уравнения. В данной статье мы рассмотрим основные техники и методы решения уравнений с дробями, а также предоставим примеры для наглядного понимания.

Основные Техники Решения Уравнений с Дробями:

1. Очистка Уравнения от Дробей:

Первым шагом в решении уравнений с дробями является избавление от них. Это можно сделать, умножив обе стороны уравнения на наименьшее общее кратное (НОК) знаменателей всех дробей. Этот подход помогает преобразовать уравнение в уравнение без дробей.

2. Приведение к Общему Знаменателю:

В случае, если дроби имеют разные знаменатели, их можно привести к общему знаменателю. Это облегчает операции с дробями и упрощает уравнение.

3. Решение Полученного Уравнения:

После того как уравнение стало лишено дробей, его можно решить с использованием стандартных методов решения уравнений, таких как применение свойств алгебры, факторизация, выделение полного квадрата и т.д.

Примеры Решения Уравнений с Дробями:

Рассмотрим уравнение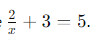

Шаг 1: Очистим уравнение от дроби, умножив обе стороны на x:

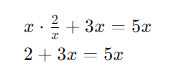
Шаг 2: Перенесем все слагаемые с x на одну сторону:

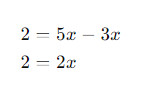
Шаг 3: Разделим обе стороны на коэффициент 2:

x=1

Таким образом, решением уравнения

Решение уравнений с дробями может быть вызовом, но с использованием правильных методов и техник, а также пониманием основных принципов алгебры, они могут быть успешно решены. Практика и углубленное изучение темы помогут в освоении этого математического навыка.