Решение линейных неравенств

Линейные неравенства впервые упоминались еще в первой половине девятого века нашей эры. Их использовали при решении задач аналитической механики. Сложно было существовать без понятий «больше» и «меньше». Неравенства были упомянуты в трактате Евдаклида. Все рассуждения он описал словами. Современные строгие знаки неравенств ввел в математику ученый Т. Гарриот, а нестрогие – Пьер Буг. Сейчас линейные неравенства изучают на уроках математики все школьники, как и уравнения. Они помогают в решении теоретических задач, в поиске ответов на практических задания.

Что такое линейные уравнения

Уравнение, содержащее неизвестную в единичной степени, называется линейным. Оно имеет вид ax + b = 0, где a, b - действительные числа, а x - переменная, которую необходимо найти. Если в равенстве одна переменная. то такое равенство называется уравнением с одной переменной. Если в уравнении есть дополнительные скобки, то их необходимо раскрыть.

У такого уравнения есть несколько вариантов решения:

1) если а ≠ 0, то оно имеет один корень

Пример:

7x + 14 = 0

7x = -14

x = -2

2) если а = 0, а в ≠ 0, то уравнение не имеет решений

0x + 1 = 0

Таких значений x нет

3) если а = 0 и в = 0, то x - любое число

0x + 0 = 0

Переменная x может иметь любое значение.

Линейные уравнения имеют свою математическую функцию. Ее можно задать формулой y = kx + b, где k и b - некоторые числа. Графиком линейной функции является прямая. Чтобы его построить, необходимы кардинаты двух точек, принадлежащих системе координат. Она может возрастать и убывать. Это зависит от коэффициента, стоящего перед неизвестной величиной. Если число к положительное, то функция возрастает, если оно отрицательная, то убывает.

Типы неравенств

Рассмотрим основные типы неравенств:

1. Линейные неравенства

В данном случае переменная находится в первой степени и не в знаменателе. Неравенство имеет вид:

ax + b > 0

где a, b - действительные числа

В линейном неравенстве две или более математических величин или выражений. Хотя бы одна из них является многочленом. Чтобы представить линейное неравенство используются различные символы:

• > больше, чем;
• < меньше, чем;
• ≠ не равно;
• ≥ больше или равно;
• ≤ меньше или равно.

Первые два знака - символы строгого неравенства, последние - нестрогого. Линейное неравенство может содержать одну или более переменных.

2. Квадратные неравенства

Неизвестная в таком неравенстве стоит во второй степени в числителе.

ax² + b - c = 0

где a, b и c - некоторые числа, причем a ≠ 0

3. Рациональное неравенство

Здесь и левая и правая части представлены алгебраическими выражениями из чисел и неизвестной, используя операции сложения, вычитания, умножения или деления. Неравенство имеет вид:

f(x) > g(x)

Где f(x), g(x) - рациональные выражения.

4. Показательное неравенство

Его можно узнать по переменной в показателе степени:

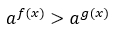
где a > 0 и a ≠ 1.

5. Логарифмическое неравенство

Переменная может содержаться как под логарифмом, так и в его основании.

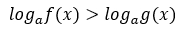
где a > 0 и a ≠ 1, f(x) > 0, g(x) > 0 .

Свойства и правила линейных неравенств

Линейные неравенства имеют свои свойства и правила. Главное их отличие — решение путем равносильных преобразований:

• любую переменную, любой член можно перенести на противоположную сторону, при этом не меняя знак самого неравенства

  ax - b > c
  ax - b > c
  ax > c + b

• обе части можно разделить или умножить на одно и то же число. Если оно положительное, то знак неравенства остается прежним, если отрицательное, то меняется на противоположный

  
  

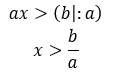
Правила сложения и вычитания.

Если к обеим частям линейного неравенства прибавить одинаковое число или выражение, то неравенство не изменится, знак останется прежним

a > b

a + x > b + x

Если из обеих частей линейного неравенства вычесть одинаковое число или выражение, но неравенство не изменится, знак останется прежним

a > b

a - x > b - x

Правила действуют при знаках <, ≤, ≥.

Как решать линейные уравнения

Решение (корень) уравнения — значение неизвестной, при котором выражение становится верным равенством.

Свободные члены необходимо перенести в левую часть, меняя их знак на противоположный. При этом получается:

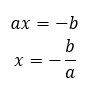
где a = 0

Можно составить определенную схему, которая поможет в решении линейных уравнений

ax + b = 0
ax = -b

Если a ≠ 0 — уравнение имеет единственный корень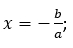 

Если a = 0 — уравнение корней не имеет;

Если a = 0, b = 0 — любое число будет корнем.

Возможно использование неравносильных преобразований при решении линейных уравнений. Для этого необходимо избавиться от знаменателей, содержащих неизвестную переменную или возвести обе части в квадрат. Название «неравносильные» предполагает, что часть корней будет потеряна.

Если значение не равно нулю, то можно применить метод интервалов. Для этого необходимо:

1. Ввести функцию y = ax + b.
2. Найти ее нули, чтобы разбить область решений на промежутки.
3. Отметить полученные корни на координатной прямой.
4. Определить знаки, отметить их на интервалах.

Равносильные преобразования

Уравнения g(x,y) = 0 и p(x,y) = 0 и равносильные если не имеют решений или их решения одинаковые.

Для решения уравнений используют равносильные преобразования:

Перенос членов уравнения на другую сторону с противоположными знаками.

Умножение или деление обеих частей уравнения на любое число отличное от нуля одновременно.

x - 3 = x²
-x² + x - 3 = 0

Перенесем x² в левую часть и изменим знак:

6x² = (24:6)
x² = 4

Так как разделила 2 части на 6, преобразование равносильное, значит их уравнения 6x² = 24 перешли к равносильному уравнению x² = 4.

Разберем примеры – задачи и их решение

В математике важен практический опыт. Начинать решать примеры рекомендуется от простых к сложным, именно так построена школьная программа по теме в 8 классе.

Рассмотрим, как решать уравнение с одной переменной.

x - 6 < 8

Используем правила переноса:

x < 8 + 6
x < 14

Изобразим числовую ось и отметим на ней получившееся число:

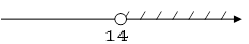
В строгих неравенствах число отмечается как «пустая» точка, потому что оно не входит в область значений.

Если неравенство не строгое, то точка «закрашенная».

Изобразим на числовой оси все решения неравенства:

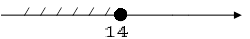
Полученный ответ также можно записать в виде (-∞; 14).

Рассмотрим другое неравенство:

3x - 18 > 0

Используем для преобразования правила переноса:

3x > 18

Разделим обе части неравенства на 3. Это положительное число, поэтому знак при этом не изменится.

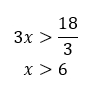
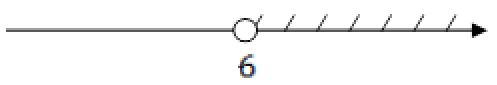
Ответ: (6;+∞)

Рассмотрим немного другой случай:

18 - 3x > 0

По правилам переноса оставляем неизвестную переменную слева, а число переносим вправо:

-3x > -18

Разделим обе части на -3, знак при этом изменится на противоположный:

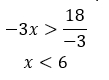
Изобразим ответ:

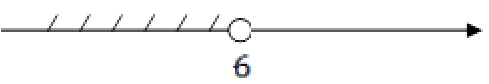
Получаем, что (-∞;6)

Неравенства на контрольных, в экзаменационных билетах обычно представлены в смешанном виде. Их необходимо привести к стандарту ax + b > 0. 

Например:

5 · (x-1) > 4 + x

Раскроем скобки:

5x - 5 > 4 + x

Воспользуемся правилом переноса:

5x - x > 4 + 5
4x > 9
x > 2,25

Ответ: (2,25;+∞)

Часто приходится решать линейные неравенства с двумя переменными. Например, x - y ≤ 5 и x + y ≤ 4. Это решается в виде системы линейных неравенств. Для этого нужно построить график. Это поможет представить решения на координатной плоскости. Для начала необходимо изобразить декартову систему координат. Неравенства преображаются в уравнения: x - y = 5 и x + y = 4.

Их необходимо рассматривать по-отдельности.

x - y = 5

Если x = 10, то y = 5;

Если x = 8, то y = 3.

Полученные точки (10;5) и (8;3) отмечаем на координатной прямой и проводим через них прямую (потому что дано линейное уравнение).

Рассмотрим второе уравнение:

x + y = 4

Если x = 2, то y = 2;

Если x = 5, то y = -1.

Отмечаем на координатной плоскости точки (2;2) и (5;-1). Проводим прямую.

Определяем их точки пересечения, это и будет решением уравнения.

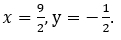
Онлайн калькуляторы для решения линейных неравенств – обзор сервисов

Symbolab — калькулятор показывает поэтапное решение линейных уравнений и неравенств. Математическую задачу можно ввести вручную или просто сфотографировать. Это облегчает работу, если время работы ограниченно.

Mathway — отличный калькулятор для того, чтобы увидеть весь процесс решения неравенства. Позволяет вычислить ответ несколькими способами: алгебраическим, с помощью графика.

SmartCalculator.online — калькулятор применяется в том случае, если необходимо только узнать ответ и записать его как в виде неравенства, так и в виде промежутка. Он не выдает пошаговое решение и график.

Math Solver — калькулятор покажет подробные этапы решения неравенства, изобразит двумерный график обеих частей. Также к каждой задаче приложены подобные видео-объяснения и связанные понятия, которые помогают разработаться в теме.

КонтрольнаяРаботаРу — калькулятор способен решить неравенства методом разложения на множители, введения новой переменной, оценки допустимых значений или функционально графическим.

Mathcracker — в калькуляторе предусмотрены все необходимые инструменты для решения линейных неравенств. Можно построить их график, видя шаги вычисления значения неизвестной переменной. Если каких-либо данных не будет хватать, калькулятор сообщит об этом.

FAQ

Для чего необходимы линейные неравенства?

Они позволяют определить максимальные и минимальные значения различных алгебраических ситуаций.

Можно ли использовать линейные неравенства в реальной жизни?

Да, они пригодятся при моделировании бизнес-задач, решении математических головоломок и т.д.

Каким способом лучше и быстрее решать линейные неравенства?

Для решения линейных неравенств подойдет как способ равносильных преобразований, так и метод интервалов. Рекомендуется решать двумя данными способами, чтобы быть уверенным в точности результатов. Важно помнить, что второй случай используется только при условии, что коэффициент при неизвестной переменной не равен нулю.

Какие частые ошибки допускают ученики, решая линейные неравенства?

Неопытные люди, «не набившие руку» часто допускают ряд ошибок. Чтобы их избежать, нужно помнить некоторые моменты:

• Возводить части неравенства в квадрат можно при условии, что они положительные;
• Из неравенства нельзя извлекать квадратный корень;
• Модуль необходимо раскрыть по всем правилам и с особой осторожностью.

В каком случае знак неравенства меняется на противоположный?

Если обе части разделить или умножить на одно и то же отрицательное число – знак меняется на противоположный. Например, 10 > 4 и умножите на -2, тогда -20 > -8. Такое неравенство неверно, значит знак изменится на противоположным чтобы значение было истина -20 > -8.

Решением линейного уравнения служит промежуток, но могут быть варианты, когда неизвестная - одно или несколько чисел. Подробное изучение правил решения линейных неравенств, много практики помогут без труда разобраться в этой теме. Онлайн-сервисы помогут удостовериться в действительности ответа.