Расстояние от точки до прямой – как определить

Найти расстояние между двумя точками не сложно. Достаточно определить длину отрезка, который их соединяет. А как искать расстояние между точкой и прямой? Рассмотрим этот вопрос на примере простых задач.

Что называется расстоянием от точки до прямой

На уроке математики школьникам объясняют, что расстоянием от конкретной точки до прямой, является длина опущенного из точки на данную прямую перпендикуляра. Перпендикуляр всегда является минимальным расстоянием от заданной точки до прямой.

Чтобы это доказать, возьмем точку М и прямую f. Из заданной точки опустим на прямую перпендикуляр, обозначив его МN. Кроме этого возьмем произвольную прямую, обозначив ее МР. Она будет являться наклонной. Исходя из свойств наклонных прямых, длина наклонной в любом случае является больше длины перпендикуляра опущенного из точки на прямую. Это нам и следовало доказать.

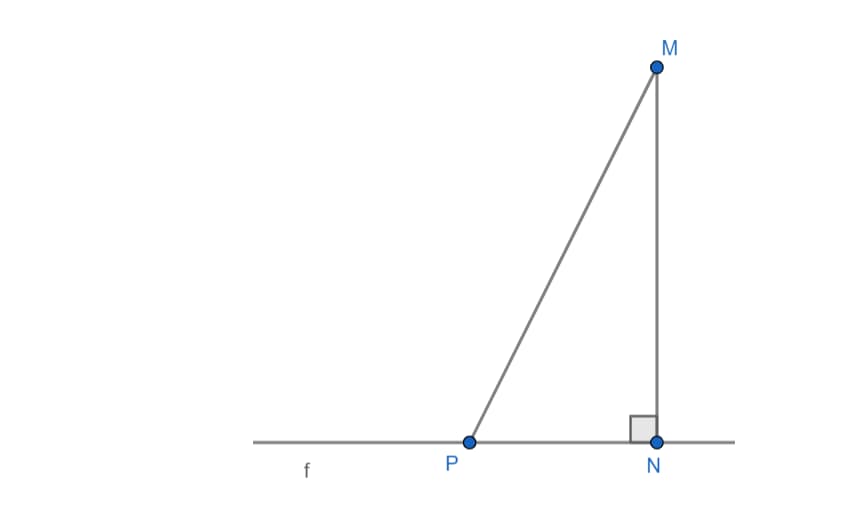
Для обозначения расстояния между нашими точкой и прямой, используем выражение: p(M,f)=MN.

Так определяется расстояние от прямой до точки в пространстве.

Расстояние от прямой до прямой

Чтобы найти расстояние между двумя разными прямыми в пространстве, которые не пересекаются друг с другом, необходимо определить длину перпендикуляра, который их соединяет.

Если необходимо определить расстояние между прямыми, одна из которых находится на плоскости, а другая располагается параллельно рассматриваемой плоскости, то следует определить расстояние от второй прямой до плоскости.

Если две прямые скрещиваются в пространстве, то расстояние между ними определяется, как расстояние от одной прямой до плоскости, в которой расположена вторая прямая. Как это сделать? Достаточно опустить из первой прямой перпендикуляр на плоскость и найти его длину.

Расстояние между параллельными прямыми

Под понятием расстояния между двумя прямыми, которые параллельны друг другу, понимают расстояние от одной прямой до другой, которая находится в той же плоскости.

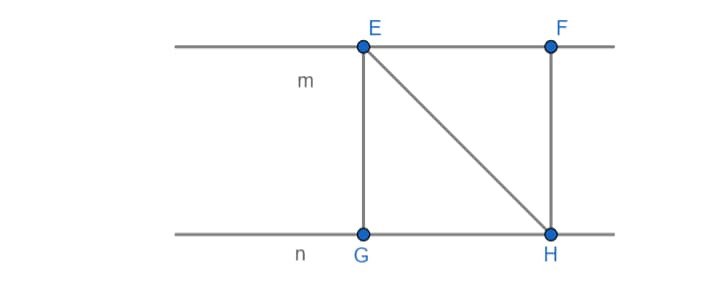
Как это проверить? Рассмотрим на представленном рисунке параллельные прямые, обозначенные m и n. Выбираем на прямой m произвольно 2 точки. Пусть это будут E и F. Из каждой из этих точек на прямую n опускаем перпендикуляры. Точки пересечения обозначаем как G  и H. Дополнительно проводим отрезок, который соединит точки Е и Р.

В результате поучаем 2 треугольника: GEN и  EFН, у которых есть общая сторона ЕН.

∠EGN= ∠EFH=90 °, ∠EHG= ∠FEG. Отсюда следует, что ΔGEH= ΔEFH, если учитывать острый угол и гипотенузу. Зная свойства равных треугольников, можно сказать, что у них будут равными все соответствующие элементы, в том числе прямые EG и FH.

Отсюда видим, что расстояние между двумя прямыми, которые находятся параллельно друг другу, это ничто иное, как длина общего для них перпендикуляра. Причем перпендикуляр можно провести в любом месте. Это можно обозначить следующим образом: p(m,n)=EG=FН.

Разберем примеры – задачи и их решение

Разобравшись, как определять расстояние между двумя прямыми, решим несколько простых задач.

Пример 1

Возьмем лист в клеточку, где размер каждой клетки равен 1*1 см. Отметим на поле произвольно точки K, M, N. Рассчитаем расстояние между точкой К и прямой MN.

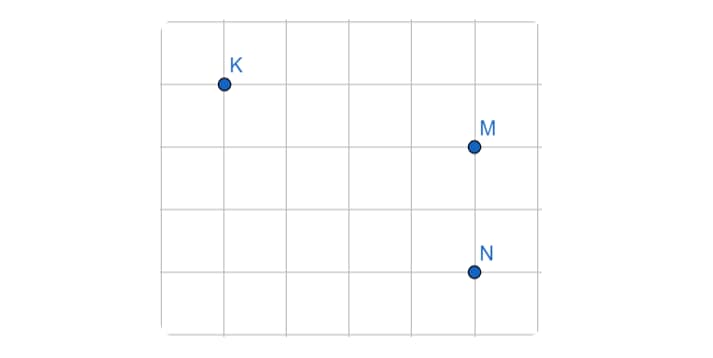
Вспоминаем из теории, что для определения расстояния между заданными точкой и прямой, необходимо из точки опустить на прямую перпендикуляр и найти его длину.

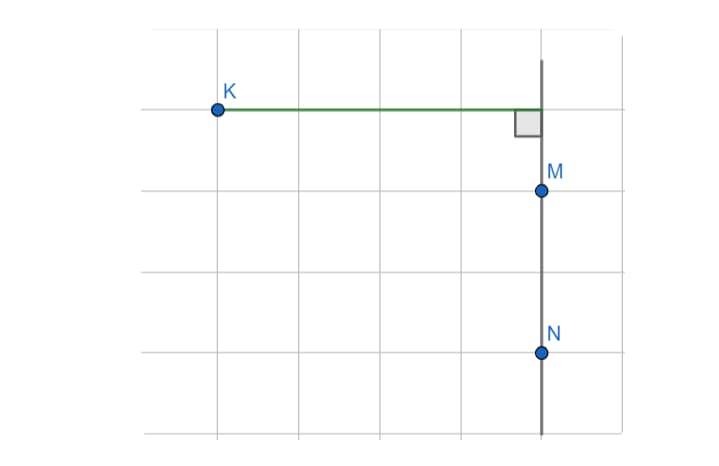
Отсюда находим ответ: 4 см.

Пример 2

Дан чертеж с нанесенными точками Q и прямой PR. Необходимо найти расстояние между ними.

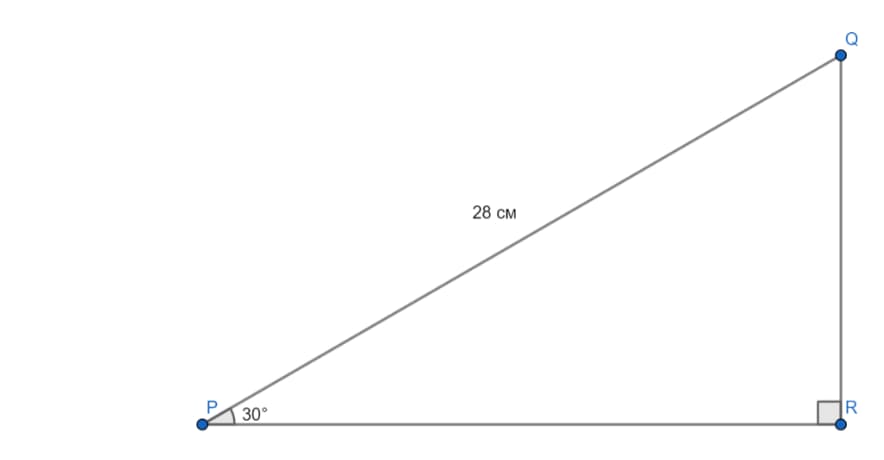
Рассмотрев чертеж можно увидеть, что отрезок QR является перпендикулярным по отношению к прямой PR. Поэтому можно сделать вывод, что QR и будет расстоянием между точкой Q и прямой PR. Так как треугольник PQR прямоугольный, а отрезок QR расположен против угла, равного 30 °, поэтому его длина равна половине гипотенузы 14 см.

Соответственно ответ: 14 см.

Пример 3

Дан равносторонний треугольник PQR с биссектрисой QS. Расстояние между точкой S и прямой QR – отрезок ST, длина которого составляет 12 см. Необходимо определить расстояние между точкой Q и прямой PR.

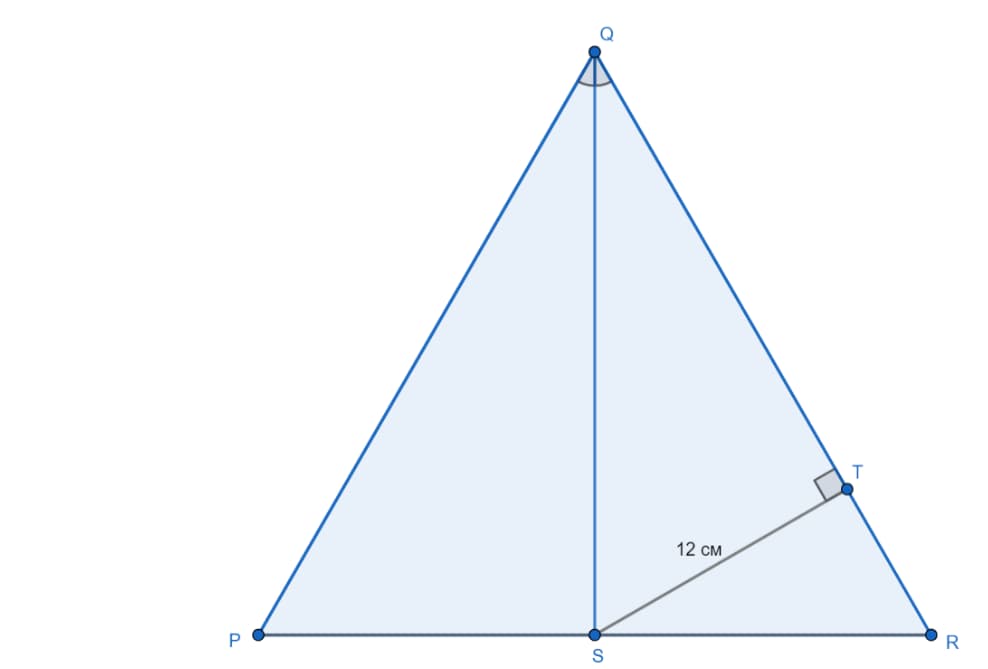
Решение будет выглядеть следующим образом:

1. Так как у нас треугольник PQR является равносторонним, значит каждый из его углов равны 60 °. ∠Р= ∠Q= ∠К=60 °. По условию у нас есть биссектриса Отсюда ∠SQR=30 °.
2. ΔQST прямоугольный, так как прямая ST перпендикулярна к QR. Также ST является катетом, расположенным против угла, равного 30 °. Отсюда находим длину QS=2 ST=24 см.
3. Исходя из того, что треугольник PQR является равносторонним, отрезок QS является не только биссектрисой, но еще и высотой треугольника. Поэтому p(Q,P,R)=QS=24см.

 Получается, что расстояние между точкой Q и прямой PR равно 24 см.

А что делать в том случае, когда провести от точки до прямой перпендикуляр невозможно физически? В таком случае может быть использована формула расчета расстояния между точкой и прямой в системе координат.

FAQ

Что такое наклонная прямая и каковы ее свойства?

Наклонной прямой называют отрезок, который выходит из определенной точки или прямой и пересекает другую прямую, но не является перпендикулярным ей. Наклонных может быть множество, а перпендикулярная прямая всего одна. При этом длина любой взятой наклонной всегда будет больше, чем длина перпендикуляра.

Что такое свойство параллельных прямых?

Абсолютно любая точка, которая находится на одной из параллельных прямых, будет равноудаленной от другой прямой.

Выводы

Для определения расстояния между точкой и прямой, достаточно провести между ними перпендикуляр и определить его длину. Для определения расстояния между двумя разными прямыми используют это же правило, если они параллельные или специальные формулы. Запомнив из можно будет легко найти расстояние между любыми прямыми, независимо от того находятся ли они в одной плоскости или в разных.