Прямоугольный параллелепипед

Понятие прямоугольного параллелепипеда широко используется в геометрии, но не в повседневной жизни. Однако нас окружают многие предметы в форме параллелепипеда. Например, данную форму имеют следующие предметы: коробки, книги, здания, холодильники, шкафы и многие другие.

Прямоугольный параллелепипед – что это такое, определение

Параллелепипед - геометрическая фигура, состоящая из четырёхугольников и отрезков, последовательно соединяющих эти четырёхугольники. Четырёхугольники ещё называются параллелограммами, которые имеют «грани», а отрезки, соединяющие их – «рёбра». Грани попарно параллельны и равны друг другу.

Рассмотрим на примере. Поверхность из 2 равных параллелограммов АВСD и А₁В₁С₁D₁ и 4 параллелограммов АВВ₁А₁, ВСС₁В₁, СDD₁С₁, DАА₁D₁.

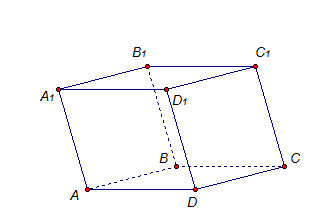
Диагонали параллелепипеда пересекаются в одной точке и этой точкой делятся пополам.

Изучение геометрической фигуры поможет понять её строение и свойства, например: объем, длины ребер, площадь поверхности, углы между гранями и другие характеристики. И также прямоугольный параллелепипед помогает в изучении многих геометрических фигур, таких как куб, квадрат, треугольник, прямоугольник, и т. д.

В изучении прямоугольного параллелепипеда есть практическое значение во многих интересных областях: строительство, дизайн, инженерия и т. д. Но также, эта фигура часто замешана в повседневной жизни.

Рассмотрим следующую ситуацию, как объяснить ребенку на простом примере ситуацию, которая могла бы произойти с каждым:

В холодильнике лежит большой прямоугольный кусок сыра. После того как отрезали кусок нужно записать, сколько съели, чтобы потом определить, когда пора идти в магазин за новым куском. Если сразу замерить длину, ширину и высоту, после того как отрежете каждый кусок рассчитывать новые данные. и родители позволили вам его есть. Но вы обязаны записывать то, сколько именно сыра было съедено, чтобы знать когда пойти в магазин. Благодаря знаниям, которые можно получить далее по статье, можно будет сделать следующее: узнать изначальные данные сыра (его длину, ширину и высоту), и после отрезания того, что вы хотите съесть - его конечные данные. Используя формулу, можно провести расчеты и научно подойти к вопросу употребления сыра.

Свойства параллелепипеда

Свойства параллелепипеда позволяют рассчитывать практически любые изменения в нём.

1. Геометрические фигуры, образующие грани параллелепипеда, представляют собой параллелограммы.
2. Грани параллелепипеда, расположенные напротив друг друга, имеют одинаковую площадь и параллельны между собой.
3. Длины любых двух диагоналей параллелепипеда совпадают.
4. Объем параллелепипеда можно вычислить, перемножив его длину, ширину и высоту.
5. Площадь параллелепипеда равна сумме площадей всех его граней.
6. Параллелепипед характеризуется наличием двенадцати ребер, восьми вершин и шести граней.

Прямой параллелепипед

Формулы для расчета площади боковой и полной поверхности, объема:

1. Площадь боковой поверхности параллелепипеда:
   Sбоковая = Периметр основания × Высота
2. Площадь полной поверхности:
   Sполная = Sбоковая + 2 × Площадь основания
3. Объем:
   V = Площадь основания × Высота

Свойства геометрической фигуры:

1. Прямой параллелепипед — параллелепипед с ребром, перпендикулярным к плоскости основания. Углы такого параллелепипеда составляют прямые (90 градусов).
2. Прямоугольный параллелепипед — фигура, все грани которой имеют форму прямоугольников. Его размеры - длины трех ребер, сходящихся в одной вершине. Является частным случаем прямого параллелепипеда.
3. Куб — параллелепипед, все грани которого представляют собой квадраты. Является частным случаем прямоугольного параллелепипеда.

Прямоугольный параллелепипед

Прямоугольный параллелепипед еще иногда называют прямолинейным, ведь у него все грани представляют собой прямоугольники, а все двугранные углы прямые. Благодаря наличию трех пар параллельных граней, прямоугольный параллелепипед симметричный. Противоположные грани прямоугольного параллелепипеда равны по площади и параллельны друг другу.

Прямоугольный параллелепипед характеризуется шестью гранями, двенадцатью ребрами и восемью вершинами. Грани прямоугольного параллелепипеда можно рассматривать как прямоугольные плоскости, а ребра – как отрезки, соединяющие вершины. Таким образом становится ясно, что:

• прямоугольный параллелепипед состоит из прямоугольников;
• прямоугольники называются гранями;
• отрезки между гранями называются рёбрами;
• углы называются вершинами;
• из свойств прямоугольников следует, что углы в параллелепипеде, также как и в них самих, будут прямыми;
• ‌грани попарно направлены друг на друга и параллельны.

Прямоугольный параллелепипед – свойства и формулы расчета

Рассмотрим основные свойства геометрической фигуры:

1. Геометрическая эквивалентность граней. Противоположные грани параллелепипеда идентичны по своим размерам и располагаются параллельно друг другу. Это обусловлено его конструкцией как призмы с прямоугольным основанием.
2. Многогранная параллельность. Параллелепипед состоит из шести граней, которые расположены попарно параллельно. Это свойство характерно для многогранников, в которых все грани параллельны попарно.
3. Прямоугольность внутренних углов. Все внутренние углы параллелепипеда прямые. Это связано с тем, что он является призмой с прямоугольным основанием.
4. Объем как произведение измерений. Объем параллелепипеда рассчитывается путем умножения его длины, ширины и высоты. Это следует из формулы объема призмы.
5. Многогранная площадь поверхности. Площадь поверхности параллелепипеда равна сумме площадей всех его граней. Это свойство выведено путем разложения параллелепипеда на шесть прямоугольников и вычисления площади каждого из них.
6. Центральное пересечение диагоналей. Диагонали параллелепипеда пересекаются в центре фигуры и имеют одинаковую длину. Более того, в точке пересечения они делятся пополам. Это свойство обусловлено симметрией параллелепипеда относительно его центра.
7. Центральная симметрия. Параллелепипед симметричен относительно середины своей диагонали. Это свойство вытекает из его симметрии относительно центра.
8. Многогранная универсальность. Любая грань прямоугольного параллелепипеда может выступать в качестве его основания. Это связано с тем, что все грани имеют одинаковые размеры.
9. Пифагорова длина диагонали. Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трех измерений этой фигуры. Это утверждение доказывается с помощью теоремы Пифагора.

Основные формулы расчета площади, объема и других параметров параллелепипеда:

1. Площадь боковой поверхности:
   Sбоковая = 2 × (высота) × (сумма длин оснований)
   где высота - высота параллелепипеда, а суммы длин оснований - сумма длин двух его сторон.
2. Общая площадь поверхности:
   Sобщая = 2 × (сумма площадей граней)
   где сумма площадей граней - сумма площадей двух оснований и четырех боковых граней.
3. Объем:
   V = (длина основания) × (ширина основания) × (высота)
4. Длина диагонали:
   D = √((длина основания)^2 + (ширина основания)^2 + (высота)^2)
5. Диагонали боковых граней:
   d1 = √((высота)^2 + (длина основания)^2)
   d2 = √((высота)^2 + (ширина основания)^2)
   d3 = √((длина основания)^2 + (ширина основания)^2).
6. Углы между диагоналями боковых граней:
   cos(α) = высота / d1
   cos(β) = высота / d2
   cos(γ) = высота / d3
7. Радиус вписанной сферы:
   r = высота / 2

Диагонали прямоугольного параллелепипеда – теорема

Диагонали — это отрезки, соединяющие противоположные вершины фигуры. Существует теорема, согласно которой квадрат длины диагонали равняется сумме квадратов трех измерений параллелепипеда:

Теорема: d² = a² + b² + c²

где:

 d — длина диагонали

 a, b, c — длина, ширина и высота параллелепипеда, соответственно

Доказательство этой теоремы опирается на геометрические свойства прямоугольного параллелепипеда.

Доказательство:

Рассмотрим треугольник ABD. Угол BAD прямой. По теореме Пифагора:

d(1)² = a² + b²

где d(1) — длина диагонали первой грани параллелепипеда.

Аналогичным образом рассмотрим треугольник B(1)BD. Угол B(1)BD также прямой. По теореме Пифагора:

d² = d(1)² + c²

Подставляя первое уравнение во второе, получаем:

d² = a² + b² + c²

Тем самым теорема доказана.

Данная теорема является обобщением теоремы Пифагора для плоских прямоугольных треугольников и находит применение в различных областях, включая геометрию, физику и инженерное дело.

Куб

Куб — это особый случай прямоугольного параллелепипеда, у которого все измерения (длина, ширина и высота) равны. Другими словами, куб — это многогранник, у которого все грани являются квадратами.

Свойства куба:

1. Квадратные грани. Куб имеет шесть граней, каждая из которых представляет собой квадрат. Площади всех граней куба равны.
2. Параллельные грани. Противоположные грани куба параллельны друг другу.
3. Прямые углы. Все углы куба, образованные двумя гранями, прямые (90 градусов). Это свойство вытекает из того, что грани куба являются квадратами.
4. Центральные диагонали. У куба четыре диагонали, которые пересекаются в центре куба и делятся им пополам.
5. Равные диагонали. Диагонали, соединяющие противоположные вершины куба, равны друг другу.

Разберем примеры – задачи и решение

Решение задач - важный фрагмент ознакомления с темой, поэтому решим несколько простых и чуть посложнее задач на темы, упомянутые выше.

1) В прямоугольном параллелепипеде длина основания равна 6 см, ширина - 4 см, а высота - 8 см. Найдите объем этого параллелепипеда.

Решение:

Для решения задачи найдем объем прямоугольного параллелепипеда по формуле:

V = a * b * h,

где a - длина основания, b - ширина, h - высота.

Подставляем данные из условия:

V = 6 см * 4 см * 8 см = 192 см³.

Ответ: объем прямоугольного параллелепипеда равен 192 кубическим сантиметрам.

2) В прямоугольный параллелепипед с основаниями 4 см и 6 см вписан шар. Найдите объем параллелепипеда, если его высота равна 8 см.

Решение:

Для начала рассмотрим формулу для объема прямоугольного параллелепипеда:

V = a * b * h,

где a и b - длины сторон основания, h - высота.

У нас дано, что a = 4 см, b = 6 см, h = 8 см.

Подставляем значения:

V = 4 * 6 * 8 = 192 см³.

Теперь найдем радиус вписанного в параллелепипед шара.

Для этого воспользуемся тем, что радиус шара равен половине высоты параллелепипеда:

r = h/2 = 8 / 2 = 4 см.

Теперь найдем объем шара, вписанного в параллелепипед. Для этого воспользуемся формулой для объема шара:

V_шара = (4/3) * π * r^3,

V_шара = (4/3) * π * 4^3 ≈ 268,08 см³.

Таким образом, объем прямоугольного параллелепипеда равен 192 см³, а объем шара, вписанного в этот параллелепипед, равен примерно 268,08 см³.

3) В прямоугольном параллелепипеде с длиной сторон 6 см, 8 см и 10 см вписана сфера. Найдите радиус этой сферы.

Решение:

Для решения задачи нам нужно использовать свойство вписанной сферы: радиус вписанной сферы в прямоугольный параллелепипед равен половине диагонали этого параллелепипеда.

r = h/2

Дано:

Длина прямоугольного параллелепипеда: 6 см, 8 см, 10 см

Чтобы найти диагональ параллелепипеда, воспользуемся теоремой Пифагора:

d^2 = 6^2 + 8^2 + 10^2

d^2 = 36 + 64 + 100

d^2 = 200

d = √200

d = 10√2 см

Теперь найдем радиус вписанной сферы, который равен половине диагонали:

r = 1/2 * d

r = 1/2 * 10√2

r = 5√2 см

Итак, радиус вписанной сферы в этот прямоугольный параллелепипед равен 5√2 см.

4) Найдите объем куба, если его площадь поверхности равна 384 квадратным сантиметрам.

Решение:

Площадь поверхности куба равна сумме площадей его граней. У куба все грани одинаковы, поэтому площадь одной грани равна площади основания.

Пусть сторона куба равна a. Тогда площадь каждой грани равна a^2.

Так как у куба 6 граней, то полная площадь поверхности равна 6*a^2.

У нас дано, что полная площадь поверхности равна 384 квадратным сантиметрам, то есть уравнение 6*a^2 = 384.

Решим это уравнение:

6*a^2 = 384

a^2 = 384 / 6

a^2 = 64

a = √64

a = 8

Таким образом, сторона куба равна 8 см. Теперь найдем объем куба.

Объем куба равен a^3:

V = a^3

V = 8^3

V = 512

Ответ: объем куба равен 512 кубическим сантиметрам.

5) В прямоугольном параллелепипеде диагональ грани АА1D1D равна 6, а АВ = 4. Найдите боковое ребро параллелепипеда.

Решение:

Так как параллелепипед прямоугольный, то все его грани — прямоугольники, а у прямоугольника, в свою очередь, обе диагонали равны. Следовательно:

А1D = AD1 = 6.

Рассмотрим диагональ А1D и боковое ребро AA1. Треугольник А1АВ — прямоугольный, так как ребро А1В перпендикулярно грани АА1В1В (по определению прямоугольного параллелепипеда). Следовательно, гипотенуза:

АА1 = √(А1В^2 + А1D^2) = √(4^2 + 6^2) = √52 = 2√13

Ответ: 2√13

6) Дано:

Прямоугольный параллелепипед ABCDA1B1C1D1 со сторонами: AB = a = 3, AD = b = 4, AB1 = c = 5

Площадь одной грани параллелепипеда S = 12

Найти:

Объем параллелепипеда

Площадь его поверхности

Решение:

Объем:

Объем параллелепипеда равен произведению его трех измерений: длины, ширины и высоты. В данном случае длина равна стороне основания a, ширина — стороне основания b, а высота — боковому ребру c.

Объем = a × b × c = 3 × 4 × 5 = 60

Площадь поверхности:

Площадь поверхности параллелепипеда равна сумме площадей всех его граней. Поскольку параллелепипед прямоугольный, все его грани являются прямоугольниками.

Площадь поверхности = 2 × (площадь основания + площадь боковой грани)

= 2 × (a × b + a × c + b × c)

= 2 × (12 + 15 + 20)

= 94

Ответ:

Объем параллелепипеда: 60

Площадь поверхности параллелепипеда: 94

Кстати говоря, если вы решили последние задачи, то возможно у вас есть шанс сдать ЕГЭ, потому что взяты они именно оттуда.

Онлайн-калькуляторы – обзор

При решении задач на параллелепипеды может потребоваться помощь дополнительных ресурсов. В интернете можно найти онлайн-калькуляторы, каждый из которых имеет свои особенности. Далее рассмотрим их с кратким описанием того, что они делают.

Простейший калькулятор, высчитывает объем параллелепипеда (хотя если внимательно прочитать формулы, то высчитать можно и на бумаге).

Сайт onlinemschool предоставляет очень много полезных калькуляторов на самые разные темы, поискав на нем, можно обнаружить калькуляторы для всего, что может понадобиться.

Сайт на котором есть самые различные калькуляторы: от дробей - до возраста или оценок.

Из приложений для расчета различных выражений, можно посоветовать:

Photomath - крайне удобное приложение, которое можно скачать из Google Play и App Store. Приложение позволяет решать большое количество разных задач. Вы так же можете сфотографировать выражение и получить подробное описание того, как оно решалось.

FAQ

Ответим на самые распространенные вопросы при изучении прямоугольных параллелепипедов:

Зачем нам нужно знать про параллелепипеды и как это может помочь в повседневной жизни?

Ответ: Параллелепипеды окружают нас всюду в повседневной жизни. Знания об этой фигуре применяются во многих науках (чаще всего в тех, которые связаны с геометрией). В жизни они почти не применяются. Но для получения аттестата и сдачи ЕГЭ очень нужны.

Какие интересные факты можно узнать о параллелепипедах?

Ответ: Практически в любом месте где бы вы ни находились, вы можете обнаружить хотя бы что-то соответствующее форме параллелепипеда. Самый большой кирпич имеет длину грани 6 метров, высоту 1 метр и ширину 3 метра. И футляры струнных музыкальных инструментов (гитара, скрипка) делают тоже в форме параллелепипеда.

Чем может быть полезно знание формул параллелепипеда?

Ответ: Знание такого базового понятия позволить с лёгкостью продолжить изучение геометрии и может потом позволить поступить на направления, связанные с архитектурой, дизайном. Таким образом, знание этой темы косвенно, но точно ведёт к будущей профессии.

Какие игры можно придумать с использованием знаний о параллелепипедах?

Ответ: Многие компьютерные игры используют параллелепипеды в формировании своих миров. К примеру, мир Minecraft - одной из самых популярных игр полностью состоит из кубов, которые в свою очередь являются частным случаем параллелепипеда.

Чем полезно изучение параллелепипедов?

Ответ: Глобально, изучение данных фигур помогает развить пространственное мышление и знакомит с трёхмерным миром самым лёгким из доступных способов. Так же, прямоугольный параллелепипед — самая удобная фигура для строительства. Даже здание, в котором вы скорее всего находитесь, при чтении данной статьи, состоит из кирпичей, которые принимают уже знакомую вам форму.

Вывод

Уже невозможно представить наш мир без концепции параллелепипедов. Они есть везде и часто встречаются в задачах. Чтобы решать такие задачи и уметь взаимодействовать с примерно половиной объектов нашего мира, нужно изучать это направление и оттачивать применение формул и свойств.