Прямоугольная система координат – ось абсцисс и ординат

В математике принято находить положение объекта на плоскости по системе координат. С помощью ее можно описать положение геометрических фигур и вычислить их свойства через решение неравенств и уравнений. Этот метод в математике называется методом алгебры.

Давайте узнаем, что это за система координат и как работать с ней.

Что представляет собой координатная система в математике?

Координатную систему создал отец аналитической геометрии — Рене Декарт. Поэтому ее еще называют декартовой системой координат.

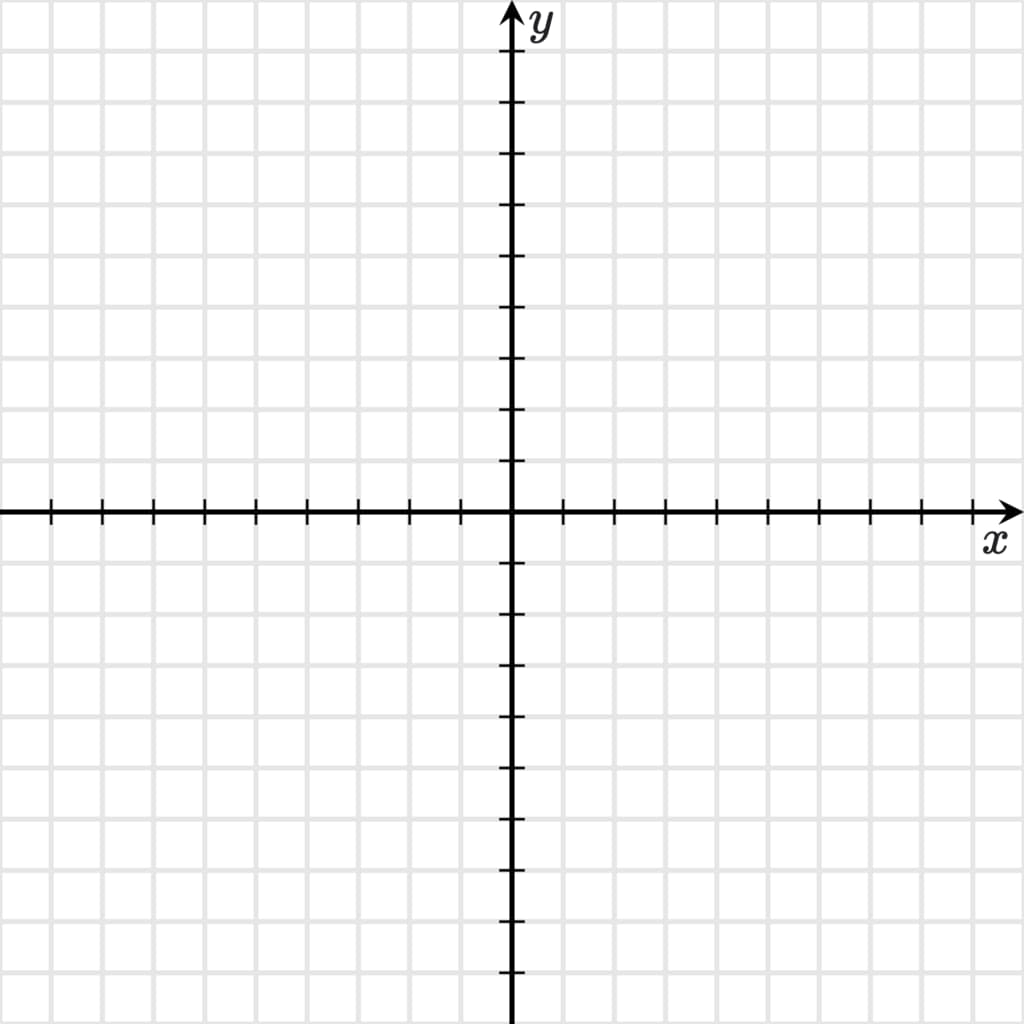
Прямоугольная система координат представляет собой пересечение двух прямых линий на одной плоскости под прямым углом. Эти линии называют осями. Система делит плоскость на 4 прямоугольных угла. Их именуют координатными четвертями.

Система координат состоит из оси абсцисс и оси ординат. Они имеют одинаковый масштаб и единицу измерения.

Положительной осью является ось абсцисс. Ее обозначают литерой «X». Она направлена слева направо. Ось ординат направлена снизу-вверх. Она обозначается литерой «Y».

Место, где пересекаются прямые, обозначают литерой «О». От пересечения начинают отсчет отрезков, на которых располагается любая геометрическая фигура.

Положительные и отрицательные значения четвертей оси координат

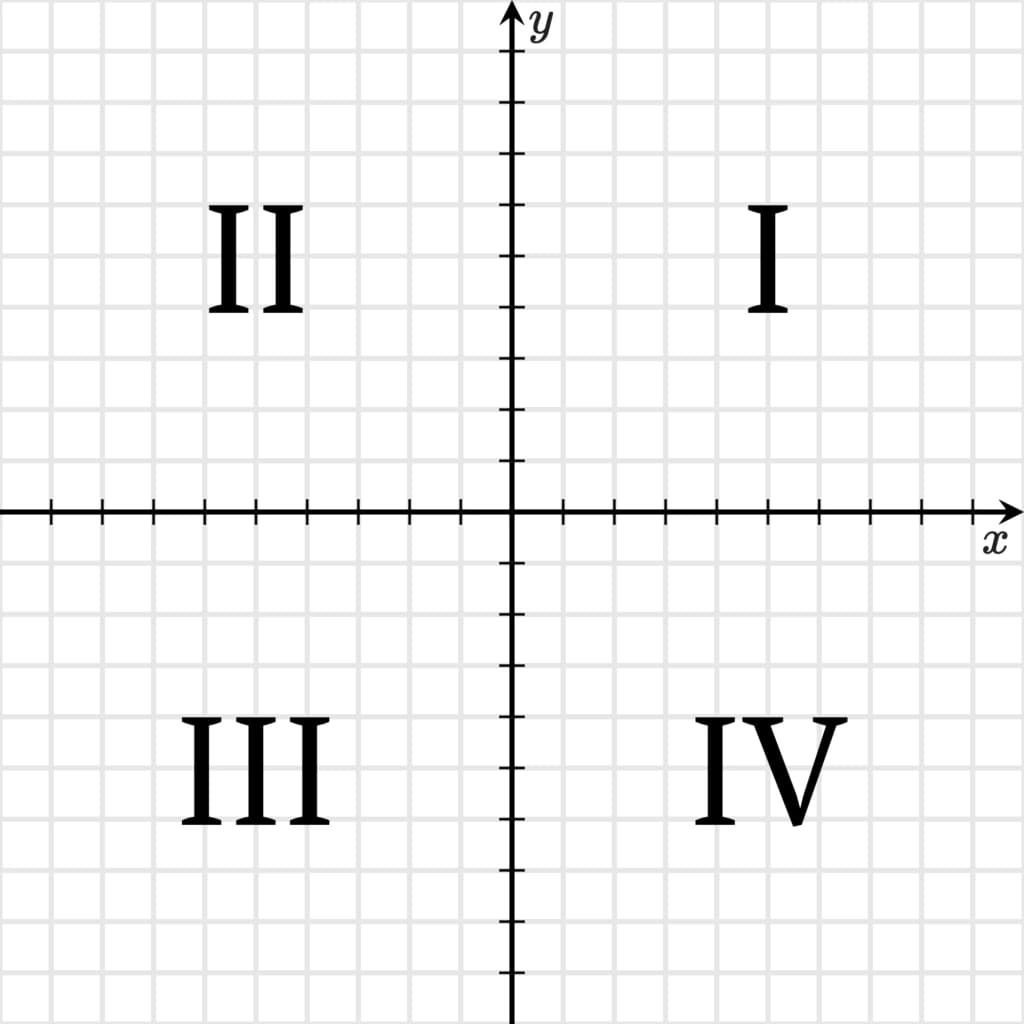
Декартову систему координат делят на 4 четверти. Четверти бывают положительными и отрицательными:

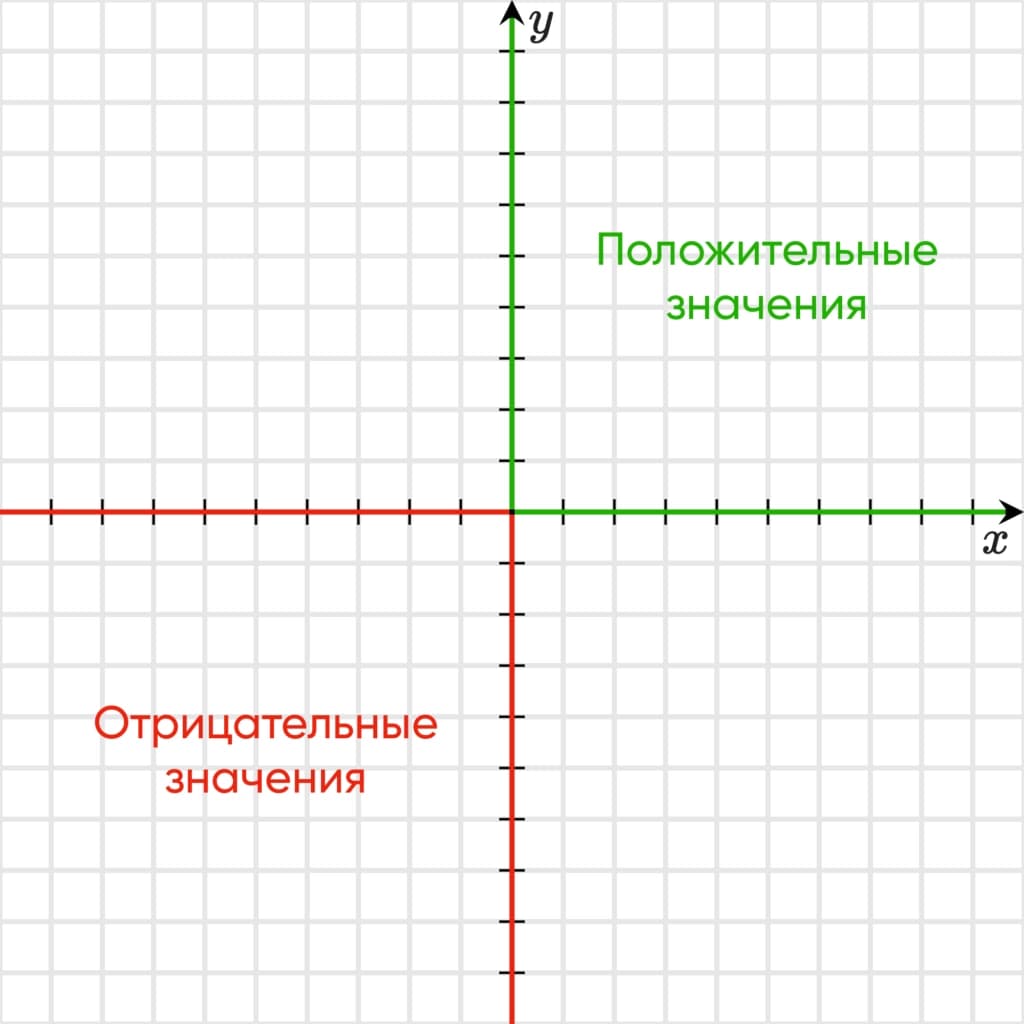
• первая четверть, обозначаемая римской цифрой I, является положительной, потому что располагается в правом верхнем углу. Так как именно верхнем и в правом направлении осей системы располагаются положительные числа;
• вторая четверть обозначается римской цифрой II и располагается в левом верхнем углу. Поэтому значения отрезка по оси «Y» будут всегда положительными, а по оси «X» — отрицательными;
• третья четверть находится в левом нижнем углу системы координат. Отрезок прямой, располагающейся в этой четверти всегда будет нести отрицательные значения, потому что в левом и нижнем направлении осей «X» и «Y» располагаются отрицательные значения чисел;
• четвертая четверть находится в правом нижнем углу. Отрезок, лежащий в этой четверти, будет нести по оси «X» положительные значения, а по оси «Y» — отрицательные.

Евклидовое пространство или система координат в трехмерном пространстве

Отличие евклидового пространства от декартовой системы координат в том, что к осям абсциссы и ординаты добавляется еще одна — ось аппликат. Она располагается взаимно перпендикулярно осям абсцисс и ординат.

В зависимости от направления евклидово пространство может быть правым или левым. Давайте определим при каких значениях она станет правой, а при каких левой:

• если повернуть ось Х против часовой стрелки на 90 градусов, то ее положение совпадет с отрицательным положением оси ординат. В этом случае трехмерная система может быть правой;
• если повернуть ось Х по часовой стрелке на 90 градусов, то ее положение совпадет с отрицательным положением оси ординат. В этом случае трехмерная система может быть левой;

Примеры с поиском расположения точек и отрезков в системе координат

Точка «А» лежит в определенной плоскости на системе координат. Чтобы узнать, в каких значения плоскости она находится, проведем перпендикулярные линии оси X и оси Y. Таким образом мы определим расположение точки в плоскости. Пусть точка А перпендикулярна числовому значению 4 на оси X, и числовому значению 5 на оси Y.

Из этого примера мы узнаем, что точка А лежит в первой четверти плоскости координат и имеет положительное значение. Для записи обозначения точки в системе координат в тетради по математике нужно прописать следующее: А (4; 5). Первым числом в скобках всегда пишем значения оси абсцисс, вторым — ординат.

FAQ

Может ли точка, располагающаяся положительной четверти декартовой системы координат, иметь отрицательные значения?

Нет, не может.

Что такое единичный отрезок на системе координат?

Единичный отрезок на системе координат является величиной, которую принимают за единицу при выполнении геометрических заданий. В прямоугольной декартовой системе координат единичный отрезок может быть отмечен на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.

Вывод

Теперь вы знаете, что такое прямоугольная декартова система координат. Еще раз изучите теорию и перейдите к решению практических задач, используя данную систему.