Признаки равенства треугольников

Признаки равенства треугольников проходят в 7 классе. Эта тема часто встречается при решении задач, в том числе, на экзаменах. Рассмотрим признаки равенства треугольников, а также разберем несколько примеров для закрепления материала.

Первый признак равенства треугольников

Суть первого признака равенства заключается в том, что если две стороны и угол между ними у одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

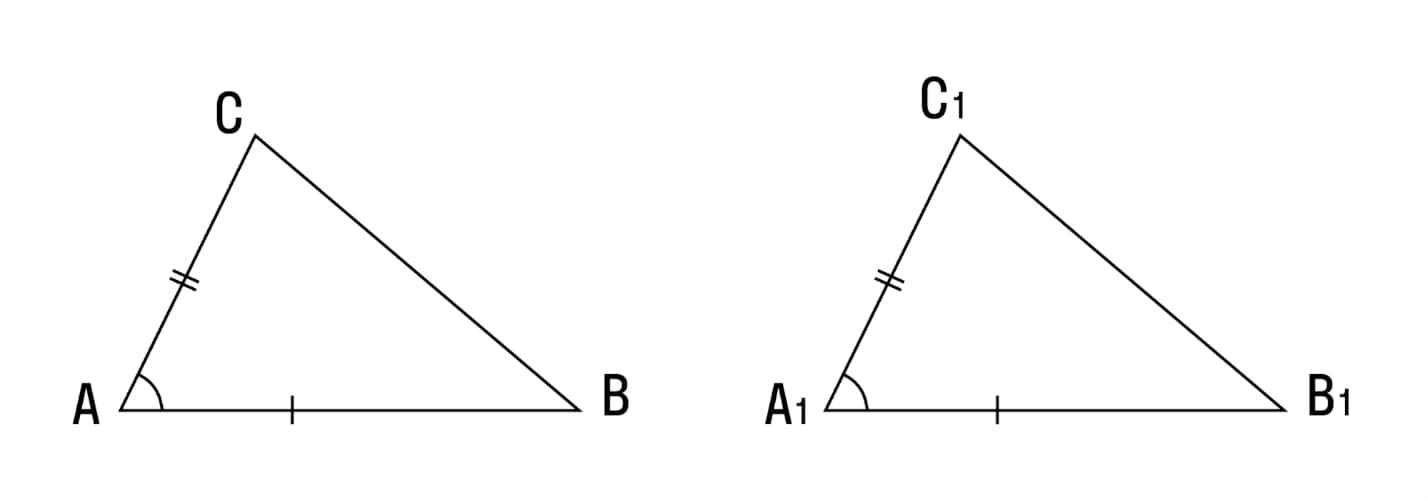
Рассмотрим такие треугольники на примере и выполним доказательство:

Даны два треугольника: ABC и A₁B₁C₁, у которых AC= A₁C₁, AB= A₁B₁, а угол А = углу A₁. Давайте докажем, что эти 2 треугольника являются равными.

Для этого наложим треугольник A₁B₁C₁ на треугольник ABC. Получится, что вершина A₁ совместится с вершиной А, сторона A₁B₁ наложится на сторону AB, а A₁C₁ на сторону АС.

Так как сторона A₁B₁ совмещается со стороной АВ, следовательно вершина В совпадает с B_1, теперь посмотрим на сторону A₁C₁, у которой вершина С₁ будет тоже совпадать с вершиной С₁.

Следовательно, происходит совмещение вершин В и В₁, С и С₁. В таком случае получается, что B₁C₁ = ВС. Так как все стороны совмещаются, а вершины совпадают в данных треугольниках, значит △ АВС = △A₁B₁C₁.

Второй признак равенства треугольников

2 признак равенства говорит о том, что если одна сторона и два прилежащих к ней угла у одного треугольника соответственно равны стороне и двум прилежащим углам второго треугольника, то такие треугольники равны.

Попробуем доказать теорему:

Рассмотрим 2 треугольника: △ АВС и △A₁B₁C_1, у которых равны сторона АС и А₁С₁, а также углы А=А₁, С=С₁.

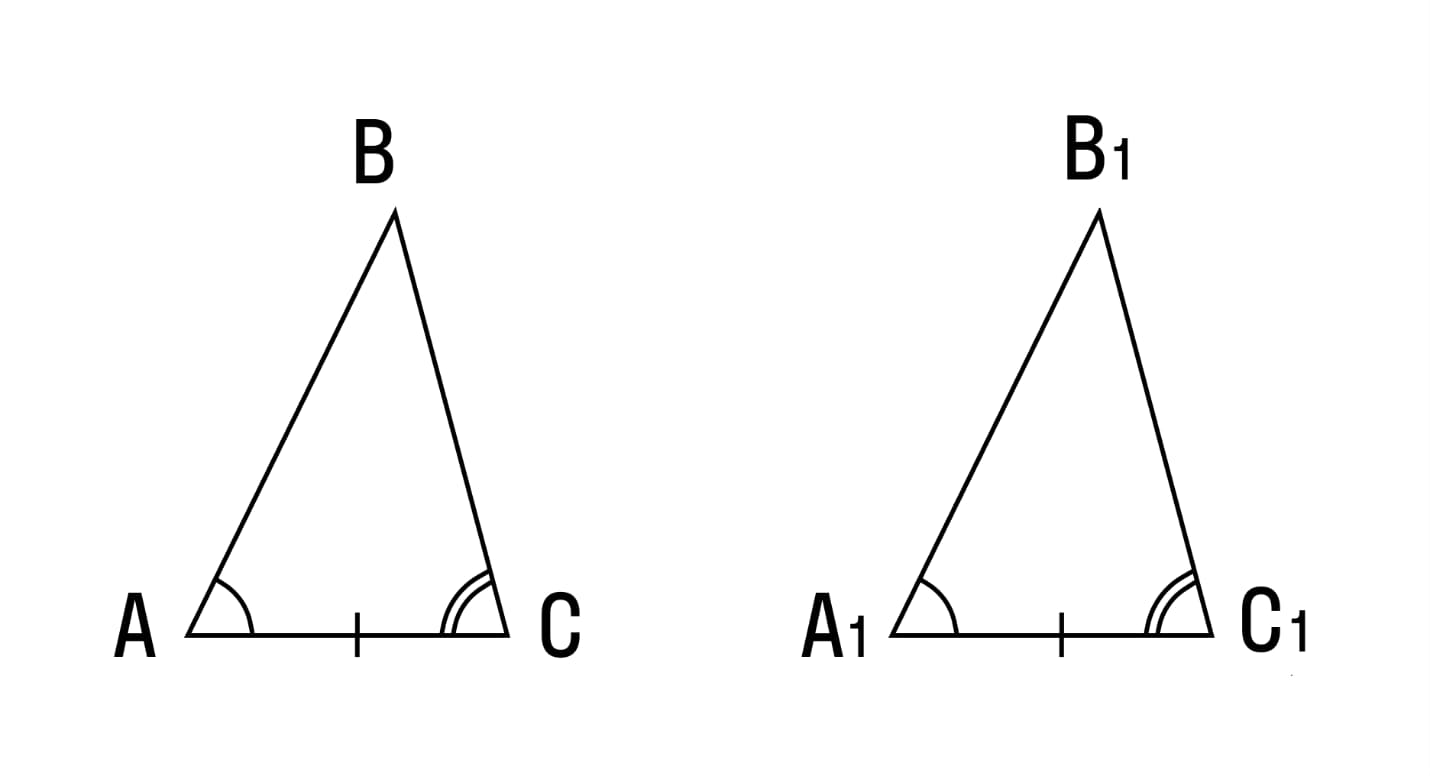
Доказательство:

1. Если наложить △АВС на △A₁B₁C₁ таким образом, что вершина А совмещается с вершиной А₁, а вершины В и В₁ лежат по одну сторону от А₁С₁.
2. Получается, что и сторона АС совмещается со стороной А₁С₁, так как мы знаем, что они равны.
3. Соответственно происходит совпадение вершины С и вершины С₁.
4. Так как угол А = углу А₁, сторона АВ накладывается на А₁В₁.
5. Так как угол С = углу С₁, сторона СВ накладывается на сторону С₁В₁.
6. Лучи АВ и СВ пересекаются в единственной точке В, а лучи А₁В₁ и С₁В₁ пересекаются в единственной точке В₁ и эти точки совпадают между собой.
7. Следовательно, △АВС полностью совмещается с △A₁B₁C₁.

Третий признак равенства треугольников

3 признак гласит, что если три стороны треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Докажем теорему:

Даны △АВС и △A₁B₁C_1, у которых:

АС=А₁С₁

АВ=А₁В₁

СВ=С₁В₁

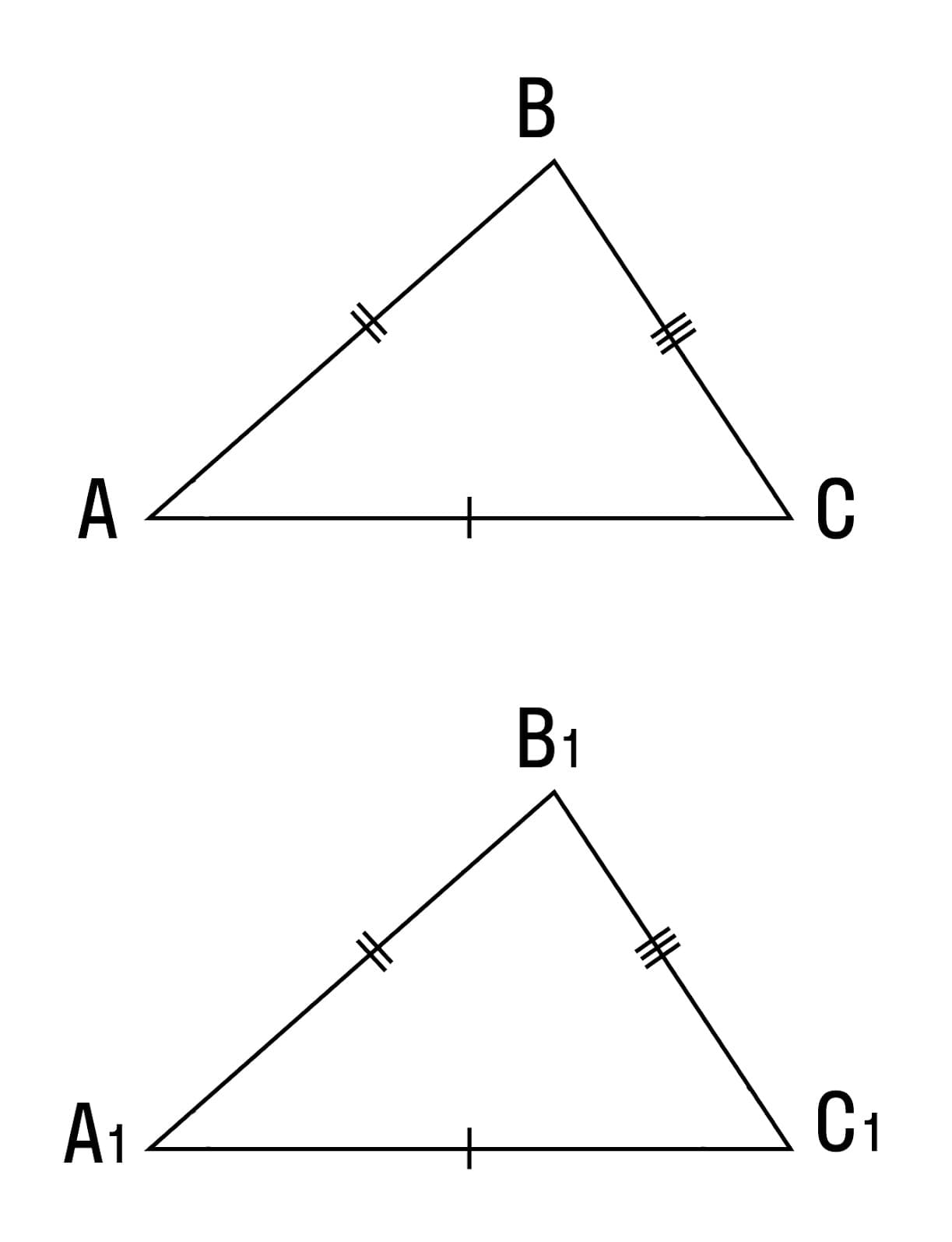
Доказательство:

1. Приложим △АВС к △A₁B₁C₁ так, чтобы вершина А совпала с вершиной А₁, вершина В – с вершиной В₁, а вершины С и С₁ легли по разные стороны от прямой А₁В₁.
2. Так как АС=А₁С₁, ВС=В₁С₁, следовательно △А₁С₁С и △В₁С₁C являются равнобедренными треугольниками.
3. Получается, что угол А₁СВ₁ равен углу А₁С₁В₁.
4. АС = А₁С₁, ВС=В₁С₁.
5. Угол С = углу С₁.
6. Воспользуемся первым признаком равенства треугольников, так как получается, что у нас 2 стороны и угол между ними равны. Следовательно, △АВС=△A₁B₁C₁.

Разберем примеры – задачи и решение

Рассмотрим несколько задач для закрепления материалов:

Задача 1.

Дано:

Равнобедренный △АВС.

Биссектрисы углов АМ и BN.

Докажите, что АМ = BN.

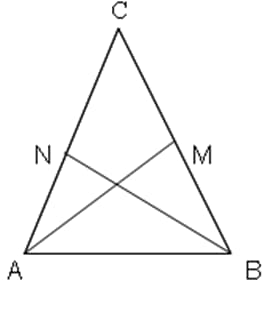
Доказательство:

Докажем, что треугольники AMB и BNA – равны:

1. Угол CAB= углу CBA, так как треугольник – равнобедренный.
2. АВ – общая сторона у треугольников AMB и BNA.
3. Угол MAB = углу NBA и = ½ угла CAB.
4. Следовательно треугольники AMB и BNA – равны (по второму признаку равенства треугольников).

Отрезки АМ и BN являются соответствующими в равных треугольниках, следовательно они равны.

Задача 2

Дано:

Треугольник АВС

Высота = биссектрисе = СР

Доказать, что если высота и биссектриса, проведенные из одной вершины равны, то треугольник является равнобедренным.

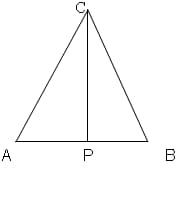
Доказательство:

Нам нужно доказать, что АС=ВС, т.е. △АВС – равнобедренный.

Для этого достаточно доказать, что △АPС=△PВС.

Воспользуемся вторым признаком равенства:

1. Угол ACP= углу BCP, так как СР – биссектриса.
2. Угол APC=углу CPB, так как СР – высота.
3. СР – общая сторона.

Следовательно: △АPС=△PВС (по второму признаку равенства), а значит АС=ВС => треугольник АВС – равнобедренный.

FAQ

В каком классе проходят признаки равенства треугольников?

Признаки равенства треугольников – тема 7 класса.

Существуют другие признаки равенства треугольников?

Да, признаков равенства треугольников намного больше, но в 7 классе пользуются преимущественно этими. Есть частные случаи, связанные с равенством прямоугольных треугольников, а также признак, по двум сторонам и углу, лежащему против большей.

Заключение

Признаки равенства треугольников – достаточно простая тема, если вникнуть в ее особенности. Однако она будет встречаться в тех или иных задачах не только в 7 классе, но и позднее. Выучить три основных признака достаточно просто, если немного попрактиковаться.