Построение графиков функций

Значительная часть математики представляет собой графическое выражение различных функций, то есть графики. Рассмотрим основные правила их построения, функциональное предназначение и специальное программное обеспечение в виде онлайн-калькуляторов, способных решить задачу быстро, точно и правильно. Тема наверняка окажется полезной школьникам и поможет лучше понять, как строитель графики функций. Что пригодится при сдаче ЕГЭ и для получения положительной оценки по одному из базовых школьных предметов.

Определение функции

Под функцией понимается зависимость одной величины (обычно обозначается как х) от другой (у). Обе они являются переменными: первая – независимой (или аргументом функции), вторая – зависимой (или значением). Если говорить математическим языком, функция является соответствием двух множеств. При этом обязательно выполняется условием, что любому элементу одного из них соответствует исключительно один элемент другого.

Функция задается с помощью правила, позволяющего определить значение зависимой переменной по значению аргумента. Решение достигается несколькими способами, каждый из которых имеет как плюсы, так и минусы. В их числе:

1. Графический. Самый наглядный. Выражается в построении графика, что является основной темой данной статьи.
2. Аналитический. Предусматривает составление формул, вычисления по которым позволяют получить зависимую переменную исходя из значения независимой. Оптимальный вариант для компактного описания соответствия. Важным плюсом становится универсальность, обеспечивающая возможность расчета в любом диапазоне.
3. Табличный. Удобный и быстрый способ определения значения функции для конкретного аргумента. Главным минусом становится ограниченность диапазона указанных переменных, которая обусловлена размерами таблицы.
4. Словесный. Наиболее сложный – как для формулирования, так и практического применения - и поэтому достаточно редко применяемый на практике.

Важно выделить еще один термин, непосредственно влияющий на процесс построения графика функции. Речь идет об области определения функции, которая представляет собой множество допустимых значений независимой переменной. Применительно к визуальному воплощению она означает проекцию функции на ось аргумента х.

Понятие графика функции

График функции представляет собой множество точек, координаты которых задаются переменными – аргументом и значением. В математической записи используются следующие обозначения:

• у=f(х) – функция или уравнение графика;
• (х; у) – координаты каждой из точек и одновременно множество точек, то есть график;
• х – независимая переменная или аргумент (абсцисса);
• у – зависимая переменная или значение функции (ордината).

Ключевое значение для визуализации и построения графика имеет правило расположения значений х и у. Первые показываются на горизонтальной оси х, вторые – на вертикальной оси у.

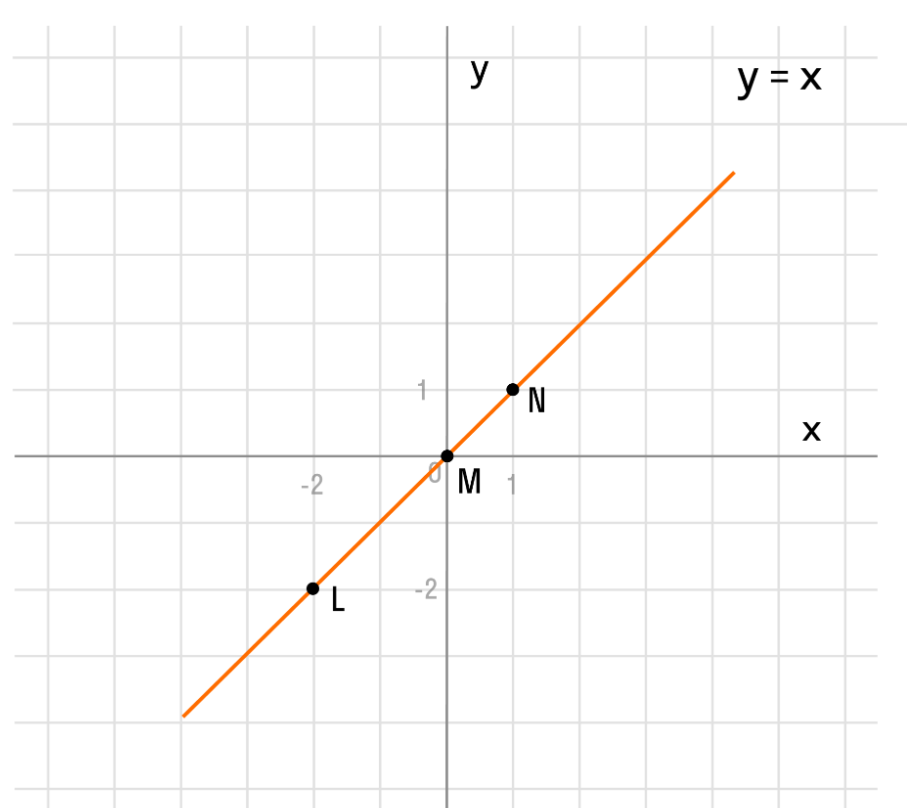
В качестве примера можно привести очень простую функцию, уравнение графика которой выглядит как у=х. Для его построения определяются координаты нескольких точек:

• L с координатами (-2; -2);
• M (0; 0);
• N (1; 1).

Далее строится координатная плоскость с указанными выше осями, на которой отмечаются точки. После этого остается их соединить, что даст на выходе полноценный график функции у=х.

Инструменты для исследования функции

Изучение графика функции предусматривает определение нескольких важных точек. В их число входят:

• стационарные (производная функции = 0);
• критические (она или =0, или не существует, то есть стационарные точки выступают как подмножество множества критических);
• экстремум – максимум или минимум значения функции в диапазоне определенного множества (это значение на графике – точка экстремума);
• нули функции – точки графика, где значение функции =0;
• асимптота – график в виде прямой, обладающей свойством стремления к нулю расстояния от точки графика до любой оси координат;
• разрыв – график, который не является непрерывным в определенной точке (для наглядности ниже приводятся примеры непрерывных функций и функций с разрывом).

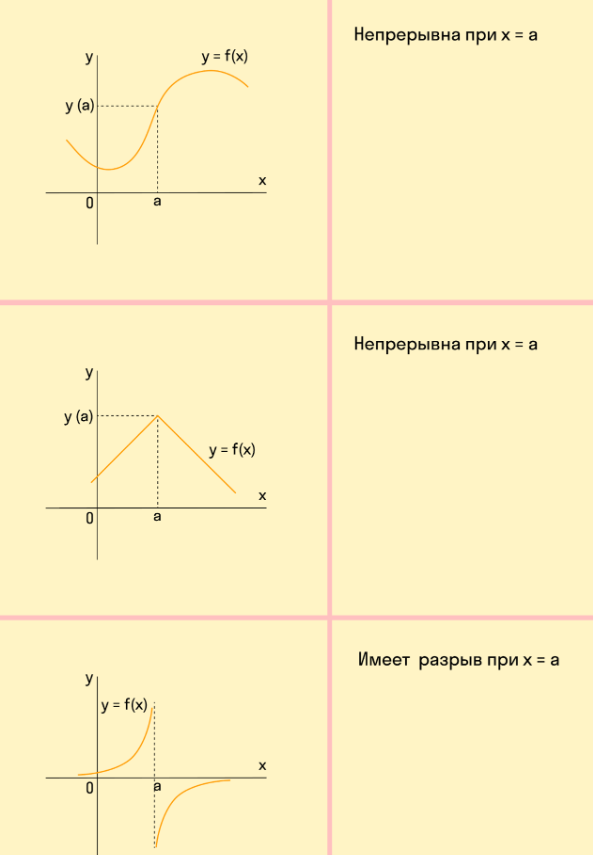
Схема построения графика функции

В общем случае для построения графика функции выполняется такая последовательность действий:

1. Поиск области определения.
2. Установление области допустимых значений.
3. Проверка функции на четность или нечетность.
4. Проверка функции на периодичность.
5. Поиск точек пересечения с осью ординат (у) – при наличии.
6. Исследование функции посредством вычисления производной, поиска критических точек, а также определения промежутков убывания и возрастания.
7. Установление промежутков так называемого знакопостоянства.
8. Поиск асимптот.
9. Непосредственное построение графика посредством нанесения на координатную плоскость точек с полученными ранее координатами.

Обзор калькуляторов

Самостоятельное построение графиков нередко становится очень сложной задачей. По самым разным причинам: начиная со сложности функции и заканчивая недостаточным уровнем подготовки школьника или даже студента. В подобной ситуации удачным ответом на вопрос, как решить проблему, становится использование специализированных онлайн-сервисов. Сегодня подобные программы можно с легкостью найти в интернете. Ниже приводятся несколько наиболее доступных и востребованных вариантов с кратким описанием возможностей, плюсов и минусов:

• https://www.yotx.ru/. Удобный онлайн-сервис, предназначенный для школьников и студентов. Позволяет быстро, бесплатно и без регистрации построить графики различных функций (включая обычные, параметрические, по точкам, с применением полярной системы координат и т.д.);
• https://www.desmos.com/Calculator?lang=ru. Специализированный калькулятор для построения графиков. Допускает размещение сразу нескольких из них на одной координатной плоскости. Для полноценного использования сервиса требуется регистрация;
• https://www.mathway.com/ru/graph. Графический калькулятор является одним из многочисленных инструментов, способных решить различные задачи при обучении в школе или вузе. Отличается разнообразным функционалом, что требует внимательного изучения возможностей программы. При грамотном использовании позволяет строить графики функций практически любой сложности;
• https://math.semestr.ru/math/plot.php. Универсальный сервис построения графиков. Предусматривает возможность как самостоятельного решения задачи, так и оформления заказа для привлечения сторонних исполнителей.

FAQ

Что такое график функции?

Это визуальное отражение соответствия независимой и зависимой переменной функций, выраженное в виде множества точек на координатной плоскости. Их координатами становятся х и у – значение первого определяется по оси абсцисс, второго – ординат.

Для чего строить графики функций?

Графический способ отражения функции позволяет наглядно представить зависимость ее переменных. Что упрощает решение множества математических и физических задач.

Можно ли воспользоваться для построения графика функции специализированными программами?

Да, сегодня в интернете можно найти множество онлайн-сервисов для построения графиков. Большая часть подобных калькуляторов работают бесплатно и не требуют регистрации.

Вывод

1. Функция представляет собой зависимость х от у, заданная по определенным правилам.
2. Графиком функции называют множество точек, координаты каждой имеют вид (х; у).
3. Местоположение точки определяется по стандартным правилам: значение аргумента откладывается на оси абсцисс, зависимой переменной – на оси ординат.
4. Построение графика функции позволяет визуально и очень наглядно продемонстрировать соответствие независимой и зависимой переменных, а также исследовать функцию с использованием специальных графических инструментов.
5. Самый простой способ построить график функции предусматривает использование специализированных калькуляторов. Подобные онлайн-сервисы – бесплатные и не требующие регистрации – можно найти в интернете в свободном доступе.