Показательные уравнения

Показательные уравнения - это тип уравнений в математике, которые содержат переменные в экспоненциальной форме. Они играют важную роль в различных областях, начиная от физики и экономики, и заканчивая информатикой и инженерией. В этой статье мы рассмотрим определение показательных уравнений, представим примеры и обсудим их применение.

Определение показательных уравнений

Показательное уравнение - это уравнение, в котором неизвестное число представлено в степенной форме. Оно обычно имеет вид:

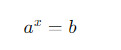
Примеры показательных уравнений

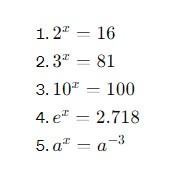
Применение показательных уравнений

1. Финансовые расчеты: Показательные уравнения используются в финансовой математике для расчета сложного процента, инвестиций и амортизации.
2. Естественные науки: В физике и химии показательные уравнения используются для моделирования роста и распада, радиоактивного распада и других процессов.
3. Инженерия: В инженерии показательные уравнения используются для анализа электрических цепей, моделирования электрических и тепловых процессов и других инженерных задач.
4. Информатика: В информатике показательные уравнения используются для описания сложности алгоритмов и анализа времени выполнения программ.
5. Экономика: В экономике показательные уравнения используются для моделирования роста населения, инфляции, процентных ставок и других экономических явлений.

Показательные уравнения являются важным инструментом в математике и ее приложениях. Они позволяют моделировать различные явления и процессы, а также решать разнообразные задачи в науке, технике, экономике и информатике. Понимание показательных уравнений помогает углубить знания в этих областях и решать сложные проблемы в реальном мире.