Показательные неравенства

Что такое показательные неравенства

Показательные неравенства - это неравенства, содержащие переменные в показателях степеней. Обычно такие неравенства решаются с помощью различных методов, таких как взятие логарифмов, использование свойств неравенств или методов анализа графиков функций.

Пример показательного неравенства:

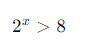
Показательные неравенства часто встречаются в математических моделях, а также в задачах на оптимизацию и анализе функций. Их решение требует понимания свойств степенных функций и методов работы с неравенствами.

Как их решать

Решение показательных неравенств включает в себя несколько шагов, в зависимости от конкретной формы неравенства и условий, накладываемых на переменные. Вот общий подход к решению показательных неравенств:

• Определите базовую основу: Изучите базовую степень, которая используется в неравенстве. Это поможет вам определить область допустимых значений переменной.
• Преобразуйте неравенство: Если это возможно, преобразуйте неравенство так, чтобы оно имело более удобную форму для анализа. Например, если возможно, приведите к общей основе.
• Решите неравенство: В зависимости от формы неравенства и условий, используйте различные методы для нахождения допустимых значений переменной x. Это может включать использование логарифмов, анализ графиков функций, проверку значений в интервалах и другие методы.
• Проверьте решение: После того, как вы найдете решение, убедитесь, что оно удовлетворяет исходному неравенству. Проверьте найденное значение переменной x подставив его обратно в исходное неравенство.
• Запишите ответ: Запишите решение в виде интервалов или в другой форме, предусмотренной условиями задачи.

Пример:

Сведение к простым формам

Показательные неравенства могут быть разного вида, и некоторые из них могут быть сведены к более простым формам для удобства решения. Вот несколько примеров таких неравенств:

1. Сведение к одной базе: Если в неравенстве присутствуют разные основания степеней, их можно привести к одной и той же базе. Например, неравенство 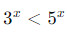 можно привести к виду 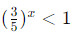, что уже удобнее анализировать.
2. Использование логарифмов: Неравенства, в которых показатели степеней содержатся в логарифмах, могут быть преобразованы с использованием свойств логарифмов. Например, 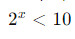 можно преобразовать к виду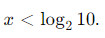
   
3. Приведение к линейному виду: Некоторые показательные неравенства могут быть преобразованы к линейным, что существенно упрощает их решение. Например, неравенство 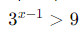 можно преобразовать к виду  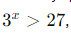что легче решить.
4. Замена переменной: Иногда замена переменной может привести неравенство к более простой форме. Например, замена 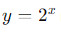 может превратить неравенство .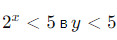