Площадь прямоугольного треугольника
Площадь прямоугольного треугольника можно находить разными способами. Для этого можно воспользоваться формулами или специальными сервисами, которые помогут рассчитать площадь онлайн быстро и просто.
Мы расскажем, как найти площадь прямоугольного треугольника, что важно понимать при расчете, какие применяются правила и формулы, какими онлайн-калькуляторами можно воспользоваться для вычислений. Это поможет вам в решении многих жизненных задач и облегчит объяснения, если вашему ребенку потребуется помощь по математике.
Основные определения
Прежде чем заниматься расчетами, нужно изучить основные понятия, которые мы будем применять:
- Треугольник – это геометрическая фигура, состоящая из трех точек, которые не лежат на одной прямой и трех отрезков, которые последовательно соединяют эти точки и ограниченной ними части плоскости.
- Прямоугольный треугольник – это треугольник, имеющий один прямой угол (90 градусов).
- Треугольника площадь прямоугольного или любого другого – это величина той части плоскости, которую он занимает. За единицу измерения площадей принимают квадрат, сторона которого равна единице измерения отрезков. Например, если за единицу измерения отрезков принят сантиметр, то за единицу измерения площадей принимают квадрат со стороной 1 см.
- Две стороны треугольника, образующие прямой угол, называются катетами.
- Сторона треугольника, которая находится напротив прямого угла, называется гипотенузой.
- Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на противоположную сторону.
- В прямоугольном треугольнике катеты являются высотами друг к другу.
Формулы для нахождения площади прямоугольного треугольника
Рассчитывать площадь можно с помощью любых формул, предназначенных для всех треугольников.
Ниже даны все формулы для нахождения площади прямоугольного треугольника. В зависимости от исходных данных применяют разные способы.
Через катеты
Основная формула нахождения площади любого треугольника звучит так:
Площадь треугольника равна половине произведения длины высоты треугольника и длины стороны, к которой проведена высота.
S = a * h / 2.
Где:
- а – любая сторона;
- h – высота, проведенная к стороне а.
Эта формула подходит любым прямоугольным, равносторонним, равнобедренным треугольникам.
Поскольку в прямоугольном треугольнике катеты являются высотами друг к другу, формулу в нашем случае можно привести в следующий вид:
Площадь прямоугольного треугольника равна половине произведения его катетов.
S = a * в / 2.
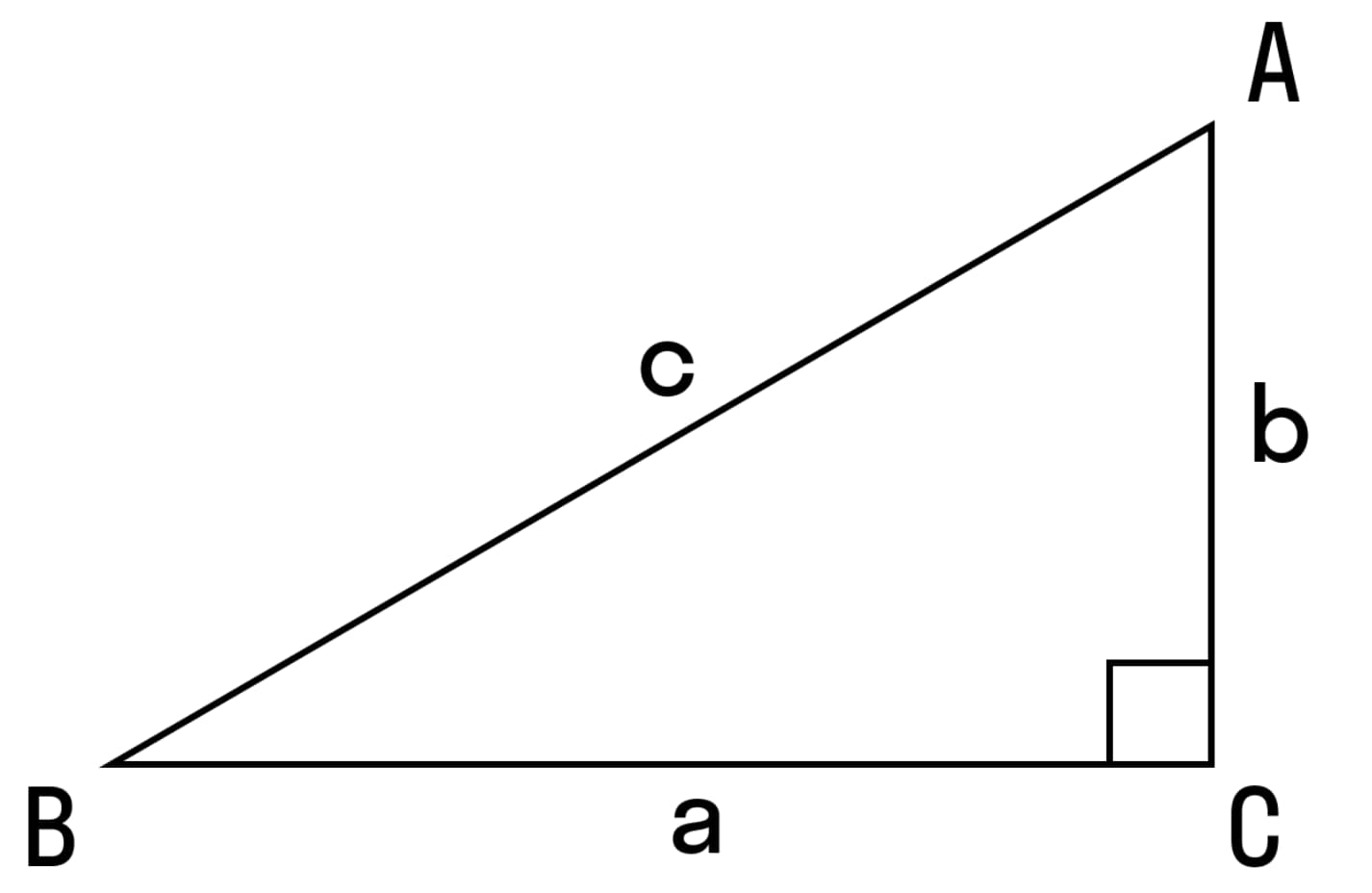
Где: а и в катеты треугольника.
По гипотенузе и высоте, проведенной к гипотенузе
Площадь прямоугольного треугольника равна половине произведения длины гипотенузы на высоту, проведенную к гипотенузе.
S = 1/2 (c × h)
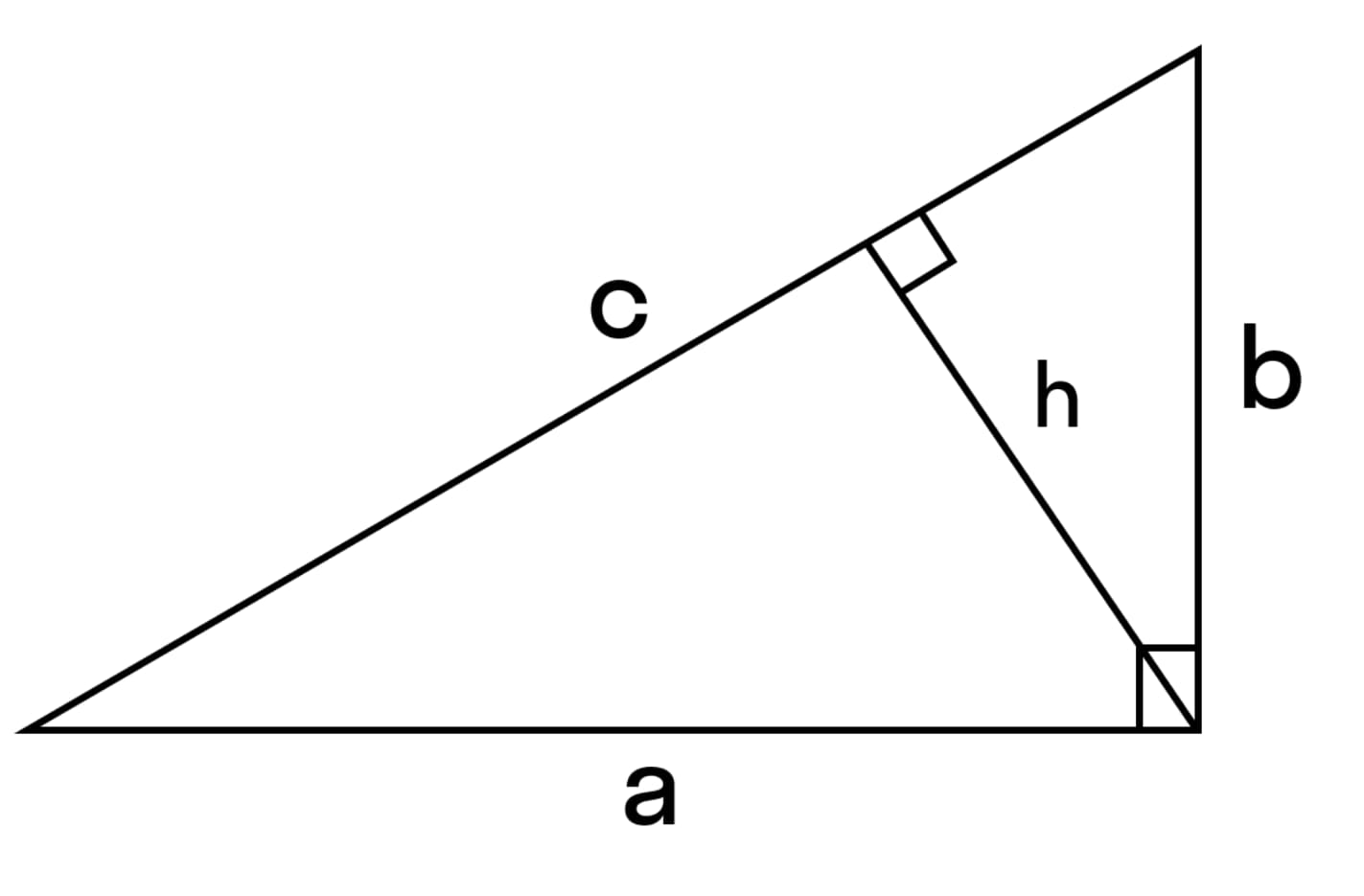
Где:
- с — гипотенуза;
- h — высота.
Через гипотенузу и острый угол
S = (c2 * sin(2α)) / 4, S = (c2 * sin(2β)) / 4
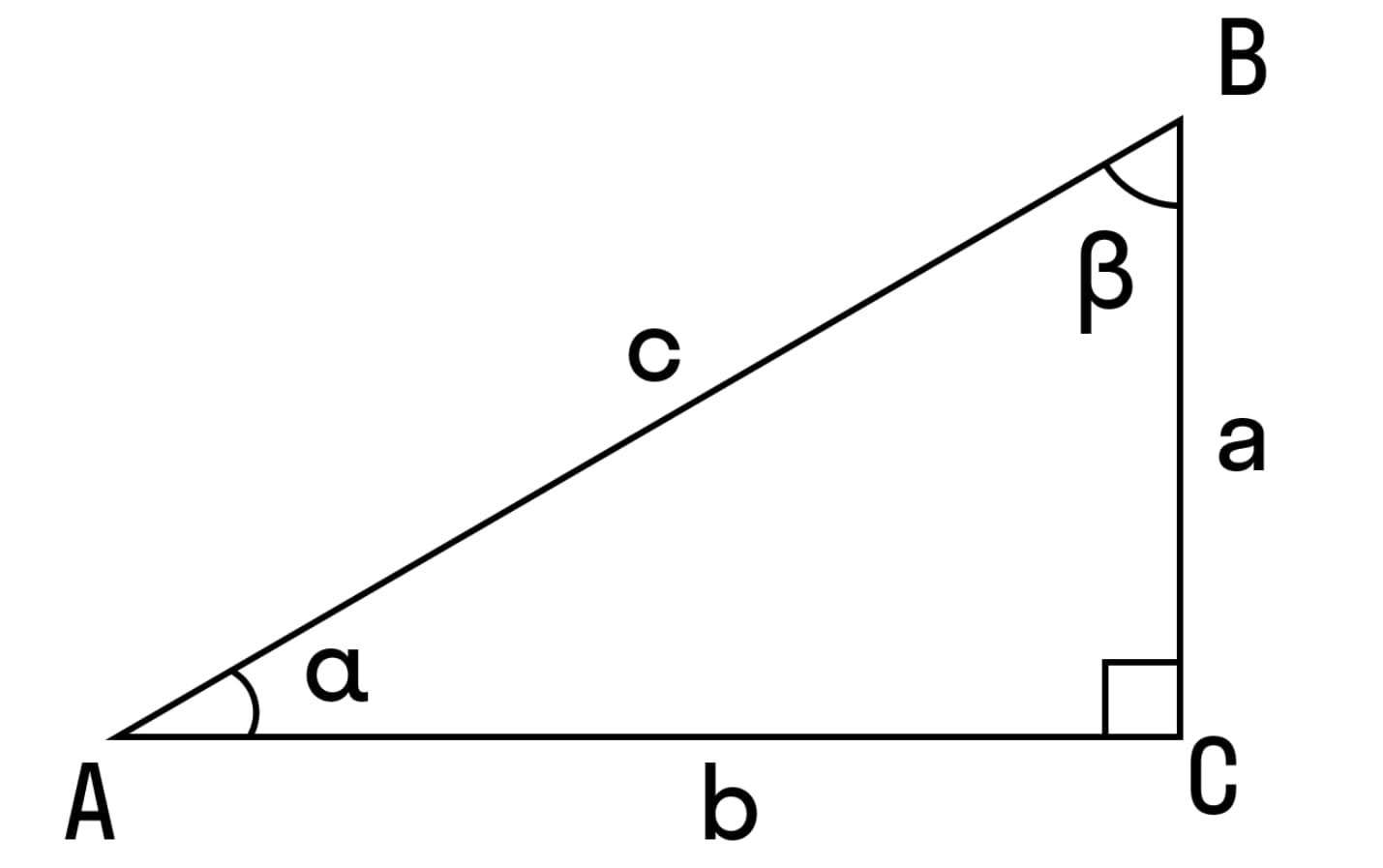
Где:
- с – гипотенуза;
- α, β – величины прилегающего к ней угла.
По катету и прилежащему углу
S = (a2 * tgα) / 2.
Где:
- а – катет;
- α – угол между этим катетом и гипотенузой.
По формуле Герона
S = √ (p * (p - a) * (p - b) * (p - c))
Где:
- а, b, c – стороны треугольника;
- p = (a + b + c) / 2 — полупериметр.
Через гипотенузу и радиус вписанной окружности
S = r * (r + c).
Где:
- r – радиус окружности;
- с – гипотенуза.
По отрезкам, на которые делит вписанная окружность его гипотенузу
S = c1 * c2
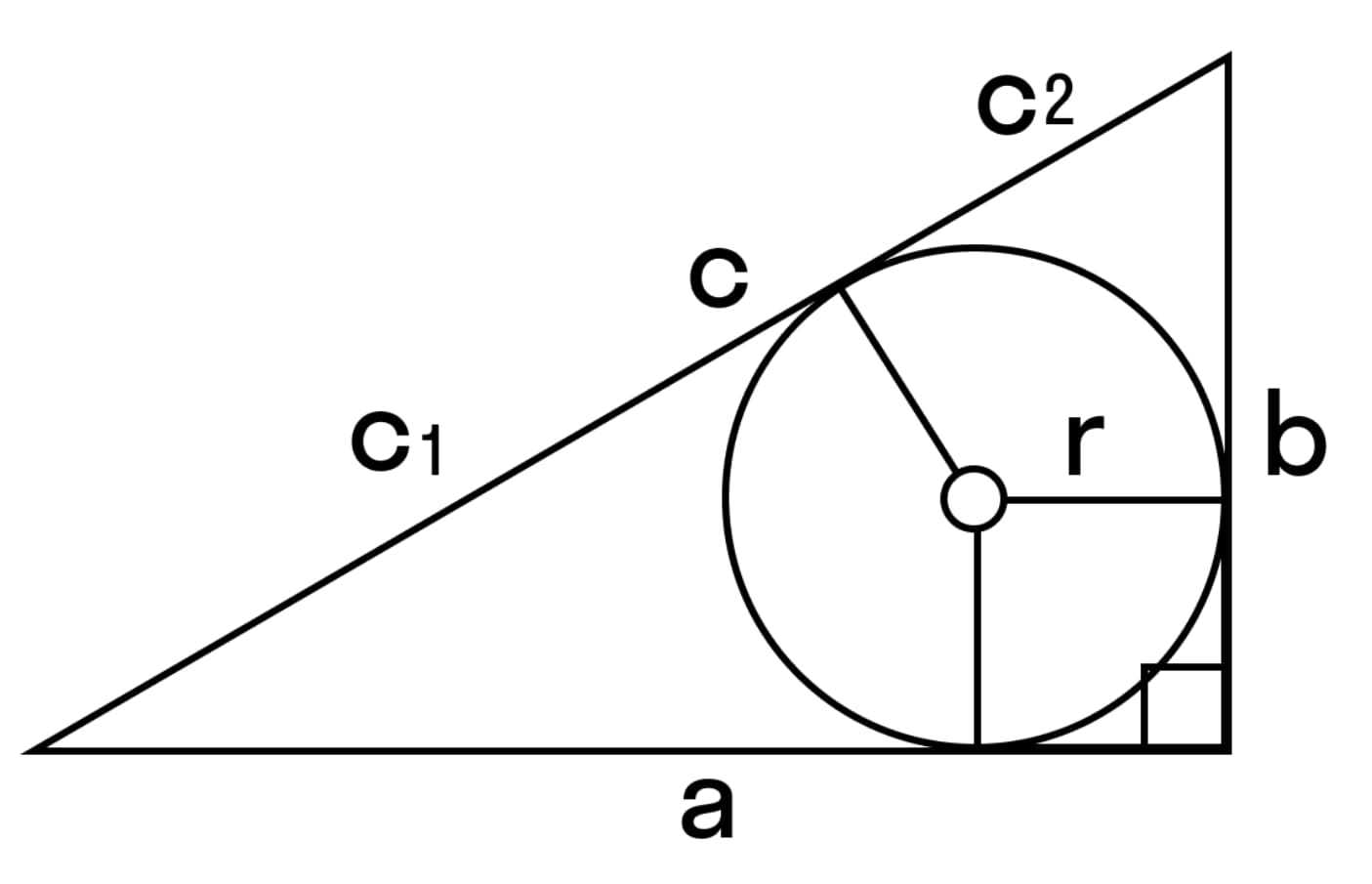
Где c1 и c2 – отрезки, на которые разделена гипотенуза точкой соприкосновения со вписанной окружностью.
Задачи и примеры
Приведем несколько задач с решениями.
Пример №1
Задание:
В прямоугольном треугольнике длина катетов составляет: а = 3 см, в = 4 см. Найти его площадь.
Решение:
Площадь равна половине произведения катетов: S = a * в / 2
Подставляем наши данные в формулу: S=3*4 / 2 = 6 (см2).
Ответ: 6 см2
Пример №2
Задание:
Дан прямоугольный треугольник BCD. Из его прямого угла высота CO, длиной 4 см, длина гипотенузы BD 8 см. Как найти площадь треугольника?
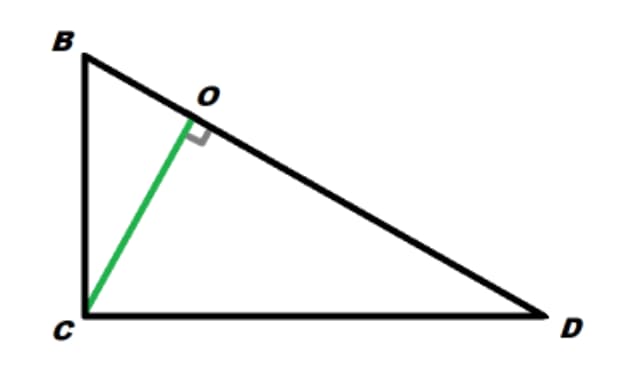
Решение:
Используем формулу S = 1/2 (c × h).
Подставим в нее наши данные: (4*8)/2 = 16 см².
Ответ: 16 см².
Онлайн калькуляторы – обзор
Для расчета площади прямоугольных треугольников можно воспользоваться специальными калькуляторами, которые предлагают специальные сервисы. Мы сделали обзор самых удобных и популярных онлайн-калькуляторов.
kalk.top
Калькулятор поможет вычислить площадь треугольника по трем сторонам и по основанию и высоте. Использовать калькулятор можно также для вычисления площади прямоугольного и других видов треугольников.
calc.by

Сalc.by поможет быстро найти площадь любого треугольника, в т. ч. прямоугольного разными способами в зависимости от известных данных. Калькулятор показывает подробное решение, поэтому его можно применять для проверки своих вычислений.
Применяемые формулы расчета площади:
- через основание и высоту;
- по формуле Герона;
- через две стороны и угол;
- через радиус вписанной окружности;
- через радиус описанной окружности.
skysmart.ru

Используя этот онлайн калькулятор, вы сможете найти площадь треугольника по:
- трем сторонам;
- двум сторонам и углу между ними;
- по стороне и опущенной на нее высоте.
Использовать калькулятор можно как для вычисления площади прямоугольного треугольника, так и других видов треугольников.
allcalc

Онлайн-калькулятор позволяет вычислить площадь прямоугольного треугольника по двум катетам.
Нужно ввести длину катета а и длину катета в и нажать «Рассчитать».
FAQ
Почему важно уметь вычислять площадь треугольника?
Умение вычислять площадь любых фигур, в т. ч. и треугольников важно при решении теоретических задач в математике и практических в повседневной жизни. Знание может пригодиться в разных сферах: строительстве, архитектуре, инженерии, дизайне и т. д.
Например, рассчитав площадь треугольника, вы сможете узнать, сколько вам потребуется материала для изготовления треугольного объекта, узнаете площадь земельного участка для постройки клумбы или целого дома.
В каких единицах вычисляют площади треугольников?
Основные метрические единицы:
- Квадратный километр (1 км²) = 1 000 000 м²
- Квадратный метр (1 м²) — основная единица измерения в системе СИ
- Квадратный дециметр (1 дм²) — в 1 м² = 100 дм² = 10 000 см²
- Квадратный сантиметр (1 см²) — в 1 м² =;10 000 см² = 1 000 000 мм²
- Квадратный миллиметр (1 мм²) — в 1 м² = 1 000 000 мм².
Старорусские единицы измерения:
- Квадратная сажень = 4, 55224 м²
- Квадратная верста = 1, 13806 км²
- Десятина = 10925, 4 м²
- Копна = 0, 1 десятины
Можно ли использовать формулу Герона для вычисления площади прямоугольного треугольника?
Формула Герона подходит для вычисления площадей любых треугольников, независимо от их формы и размеров сторон, в т. ч. и прямоугольного.
Вывод
- Знать и уметь вычислять площадь треугольника полезно не только школьникам для успешной аттестации, но и всем взрослым в повседневной жизни.
- Для расчета можно воспользоваться специальными онлайн-калькуляторами, но полезнее знать, понимать и уметь выводить формулы расчета.
- В зависимости от исходных данных применяют разные формулы вычисления площади.
- Основная формула: значение площади треугольника прямоугольного равно произведению длин его катетов, разделенному на 2 – S = a * в / 2. Где: а и в – катеты.
- Не обязательно учить формулу расчета площади прямоугольного треугольника наизусть. Зная формулу расчета площади любого треугольника и понимая значения основных величин, вы легко сможете вывести эту формулу самостоятельно.

