Все что нужно знать школьникам о площади круга

Школьникам важно знать основные понятия и формулы вычисления площади различных геометрических фигур. Эти знания пригодятся как на экзаменах, так и в будущей взрослой жизни.

В этой статье мы расскажем все что нужно о вычислении площади круга, поможем освоить формулу и посмотрим обзор на самые популярные калькуляторы, упрощающие определение площади.

Основные понятия

Площадь круга – одно из важнейших понятий в геометрии. Для того, чтобы точно определить площадь круга, необходимо знать несколько основных понятий, которые позволяют провести вычисления с высокой точностью.

Вот основные понятия:

• Окружность – это геометрическая фигура, состоящая из всех точек в плоскости, которые находятся на одинаковом расстоянии от центральной точки, называемой центром окружности. Окружность является замкнутой кривой, не имеющей ни начала, ни конца. Площадь окружности вычисляется так же как и площадь круга.
• Круг – это геометрическая фигура, ограниченная окружностью. Другими словами, круг представляет собой все точки, которые находятся на одинаковом расстоянии от центра окружности. Центр круга совпадает с центром окружности.
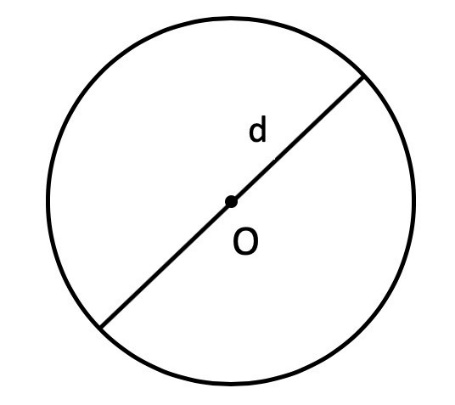
• Диаметр – это отрезок, заключенный между двумя точками на окружности и проходящий через ее центр. Диаметр является наибольшим возможным расстоянием между двумя точками на окружности. Он равен удвоенному значению радиуса окружности. Обозначается буквой «d».
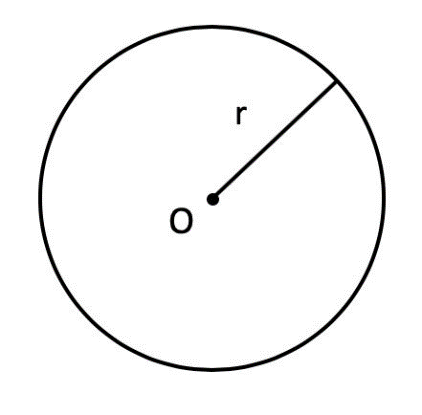
• Радиус – это расстояние от центра круга до самой внешней точки на его окружности. Обозначается обычно буквой «r». Зная значение радиуса, мы уже можем приступить к вычислению площади круга.
• Площадь круга – это мера плоской области, заключенной внутри окружности. Измеряется в квадратных единицах (например, квадратных метрах или квадратных дюймах) и представляет собой площадь поверхности, полностью заполненной кругом. Формула «Площадь круга» делится на три варианта.

Формула вычисления площади круга

Существует несколько формул для вычисления площади круга:

Вычисление площади через радиус: S = π * r²

Вычисление площади через диаметр: S = (π * d²) : 4

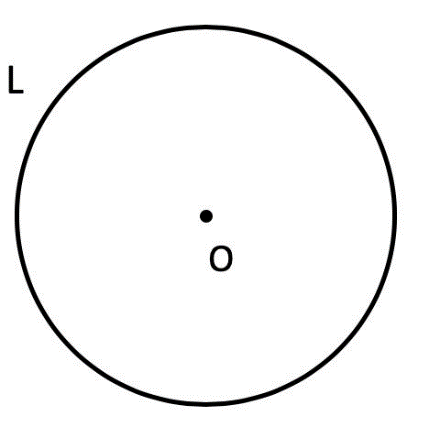
Вычисление площади круга через длину окружности: S = L² : (4 * π)

Расшифровка значений символов:

• S – площадь круга;
• r – радиус;
• d – диаметр;
• π – константа, выражающая отношение длины окружности к диаметру, равна приблизительно 3,14;
• L – длина окружности.

Основные единицы измерения:

• мм² (квадратный миллиметр);
• см² (квадратный сантиметр);
• дм² (квадратный дециметр);
• м² (квадратный метр);
• км² (квадратный километр).

Как определить площадь круга

Разберем как определить площадь круга по каждой из трех формул.

По радиусу

Для вычисления площади круга с помощью формулы S = π * r² необходимо:

• Найти радиус круга. Это может быть указано в условии задачи или измерено на рисунке.
• Возвести радиус круга в квадрат – r².
• Умножить полученное значение на константу π, чтобы найти площадь S.

Пример:

Пусть задан круг с радиусом r = 5 см. Чтобы вычислить площадь этого круга, подставим значение радиуса в формулу:

S = 3,14 * 5²

S = 3,14 * 25

S = 78,5 см²

Таким образом, площадь круга с радиусом 5 см составляет 78,5 см².

По диаметру

Чтобы найти площадь круга формула через диаметр меняется на S = (π * d²) : 4. Для расчета необходимо:

• Найти диаметр круга. Это может быть указано в условии задачи или измерено на рисунке.
• Возвести диаметр круга в квадрат – d².
• Умножить полученное значение на константу π и разделить все на 4, чтобы найти площадь S.

Пример:

К примеру, давайте вычислим площадь круга с диаметром d = 10 см. Чтобы вычислить площадь этого круга, подставим значение диаметра в формулу:

S = (π * 10²) : 4

S = (π * 100) : 4

S ≈ 78,54 см²

Таким образом, площадь круга с диаметром 10 сантиметров равна примерно 78,54 см².

По длине окружности

Для вычисления площади круга с помощью формулы S = L² : (4 * π) необходимо:

• Найти длину окружности. Это может быть указано в условии задачи.
• Возвести длину окружности в квадрат – L².
• Разделить полученное значение на константу π, умноженную на 4, чтобы найти площадь S.

Пример:

Рассчитаем площадь круга, если его длина составляет 20 см. Чтобы вычислить площадь этого круга, подставим значение длины окружности в формулу:

S = 20² : (4 * π)

S = 400 : 12,6

S ≈ 32 см²

Таким образом, площадь круга с длиной окружности 20 см. равна примерно 32 см².

Калькуляторы площади круга – обзор

Онлайн-калькуляторов, позволяющих рассчитать площадь круга очень много. Мы подобрали самые популярные из них:

• Calc.by – онлайн калькулятор для расчета площади круга. Рассчитать площадь круга можно двумя способами: через радиус и диаметр круга. После выбора вариант расчета, задайте радиус или диаметр и нажмите кнопку "Рассчитать". Калькулятор выведет результат расчета площади, а также покажет подробное решение, с помощью которого можно посмотреть, как был получен результат.
• OnlineMSchool – благодаря этому калькулятору, вы сможете найти площадь круга зная его радиус, диаметр или длину окружности и получите детальное пошаговое решение примера, которое позволит понять алгоритм решения таких задач и закрепить пройденный материал.
• Ecalc – калькулятор расчета площади круга по диаметру, через радиус или длину окружности. Здесь можно не только рассчитать площадь, но и изучить теоретическую часть, касающуюся геометрии, а также посмотреть ответы на частые вопросы по теме.

FAQ

Для точности расчета достаточно ли использовать только одну формулу с определенным значением?

Да, достаточно. Не важно по какой формуле вы рассчитываете площадь, в каждом из трех вариантов ответ будет одинаковым.

Как найти площадь круга другими способами?

Есть, например, метод Леонардо да Винчи или приближение площади круга с помощью прямоугольников. Но эти способы не так точны и не нужны для школьной программы.

Вывод

• Зная формулу и способы вычисления площади круга, можно эффективно решать задачи, связанные с данной геометрической фигурой.
• В нашей статье можно найти все основные способы вычисления площади круга по разным формулам и с примерами решения задач.
• Для тех, кто хочет упростить процесс вычисления, мы нашли онлайн калькуляторы, предоставляющие возможность рассчитывать площадь круга автоматически.