Площадь геометрических фигур

Свойства площади многоугольника

Площадь многоугольника - это важная характеристика, которая определяет, сколько плоскости занимает этот многоугольник. Вот несколько свойств площади многоугольника:

• Аддитивность: Площадь многоугольника можно выразить как сумму площадей его частей. Если многоугольник разбит на несколько частей (например, треугольники или прямоугольники), то его площадь будет равна сумме площадей этих частей.
• Неотрицательность: Площадь многоугольника всегда неотрицательна. Она может быть равна нулю, если многоугольник вырожденный или состоит из вырожденных фигур, но никогда не может быть отрицательной.
• Инвариантность при параллельном переносе и вращении: Площадь многоугольника остается неизменной при параллельном переносе (сдвиге) его точек или при вращении вокруг некоторой оси.
• Линейная аддитивность: Если многоугольник делится на два или более непересекающихся многоугольника, то его площадь равна сумме площадей этих многоугольников.
• Площадь выпуклого многоугольника: Площадь выпуклого многоугольника всегда меньше площади любого другого многоугольника, который содержит его внутри себя.
• Площадь невыпуклого многоугольника: Площадь невыпуклого многоугольника может быть определена как сумма площадей его выпуклых частей минус сумма площадей его вогнутых частей.

Нахождение площади геометрических фигур

Прямоугольник

• Площадь прямоугольника вычисляется как произведение его длины L на ширину W:
  S=L×W

Квадрат

• Площадь квадрата равна квадрату длины его стороны a:
  
  

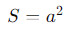
Треугольник

• Площадь треугольника можно найти, используя формулу Герона, если известны длины его сторон a, b и c, либо используя высоту ℎ и одну из сторон:
  
  

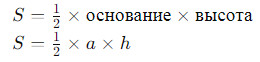
Круг

• Площадь круга вычисляется по формуле:
  
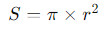
  где π - математическая константа, приблизительно равная 3.14159, а r - радиус круга.

Параллелограмм

• Площадь параллелограмма равна произведению длины его основания b на высоту ℎ
  S=b×h

Трапеция

• Площадь трапеции вычисляется как среднее арифметическое длины ее двух параллельных оснований a и b, умноженное на высоту ℎ
  
  

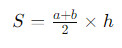
Это основные формулы для вычисления площади геометрических фигур.