Параллелограмм

Параллелограмм объективно считается одной из самых распространенных геометрических фигур. Изучение которой входит в программу 8 класса. Рассмотрим более подробно, что представляет собой параллелограмм, в чем состоят его свойства, каковы основные признаки и как рассчитывается площадь фигуры.

Определение

Параллелограммом называют плоский четырехугольник, противоположные стороны которого имеют одинаковую длину и расположены параллельно друг другу. Важно отметить, что под данное определение подходят сразу несколько фигур, еще более распространенных и часто встречающихся. Речь идет о квадрате, прямоугольнике и ромбе, который являются частными случаями параллелограмма.

Важное значение для лучшего понимания рассматриваемой фигуры имеют диагонали и биссектрисы. Поэтому имеет смысл уделить им несколько больше внимания.

Под диагональю понимается отрезок, соединяющие две вершины параллелограмма, расположенные напротив друг друга. Нехитрый расчет показывает, что каждая фигура имеет два подобных отрезка. С помощью диагоналей формулируется три свойства параллелограмма:

1. Точка пересечения делит диагонали пополам.
2. Каждая из диагоналей фигуры разделяет параллелограмм на два одинаковых треугольника.
3. Сумма квадратов диагоналей равняется умноженной на 2 сумме квадратов двух смежных сторон фигуры.

Биссектрисой называют отрезок, проведенный из вершины к одной из двух противоположных сторон параллелограмма и разделяющий угол на две равные части. Биссектриса параллелограмма обладает следующими свойствами:

1. Ее построение отсекает от основной части фигуры треугольник, который является равнобедренным.
2. Биссектрисы, которые построены из углов, прилегающих к одной стороне фигуры, пересекаются, причем под углом в 90 градусов, то есть прямым.
3. Биссектрисы из противоположных углов параллелограмма имеют равную длину и параллельны друг другу.

Свойства параллелограмма

Параллелограмм обладает несколькими свойствами, основные из которых необходимо обязательно и очень внимательно изучить. К ним относятся такие:

1. Противоположные стороны фигуры равны (то есть для параллелограмма AВCD: AB = DC и AD = ВС).
   
   
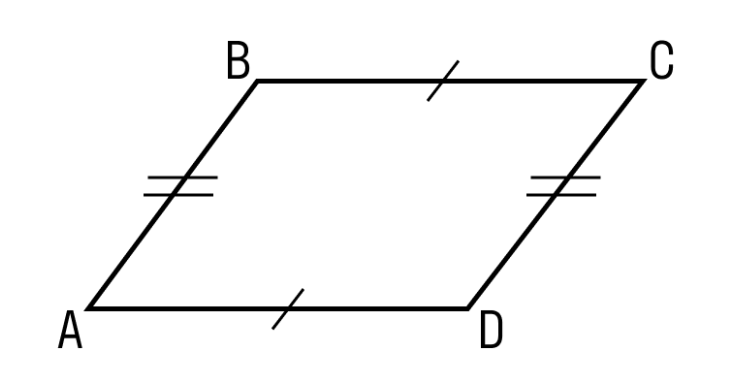
2. Ее противоположные углы также равны.
3. Точка пересечения диагоналей делит каждую на две равные части (свойство упомянуто выше при описании диагоналей параллелограмма).
4. Диагональ делит фигуру на два одинаковых треугольника (аналогично).
5. Сумма углов, прилегающих к одной стороне параллелограмма, составляет 180 градусов.
6. Сумма квадратов диагоналей равняется умноженной на 2 сумме квадратов двух смежных сторон фигуры (также упоминается выше в свойствах диагоналей фигуры).

Исходя из двух первых свойств параллелограмма, формулируется теорема, которая декларирует равенство противоположных сторон и углов фигуры. Она с легкостью доказывается на основании знаний, уже полученных школьниками к 8 классу.

Признаки параллелограмма

Принято выделять три главных признака параллелограмма, позволяющих выделять его среди других геометрических фигур:

1. Четырехугольник, у которого две расположенные друг напротив друга стороны параллельны и равны, является параллелограммом.
2. Четырехугольник, у которого две расположенные друг напротив друга стороны попарно равны, является параллелограммом.
3. Четырехугольник, диагонали которого делятся пополам в точке пересечения, является параллелограммом.

Как найти периметр и площадь?

Периметром называют сумму длин всех сторон геометрической фигуры. Применительно к параллелограмму формула расчета достаточно проста: необходимо сложить длину непараллельных стороны фигуры, после чего умножить полученный результат на два, то есть:

P= 2 * (a + b), где P традиционно обозначает периметр, а и b – длина двух непараллельных, то есть прилегающих сторон параллелограмма.

Площадью называют пространство, которое располагается внутри границ геометрической фигуры. Применительно к параллелограмму она рассчитывается несколькими способами. Чаще всего применяются три из них:

1. S = а * h, где S – это площадь (здесь и далее), а – одна из сторон, h – высота, опущенная на эту сторону.
   
   
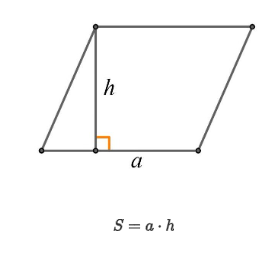
2. S = а * b * sin α, где а и b – прилегающие стороны, α – угол между ними.
3. S = 0,5 * (d1 * d2) * sin β, где d1 и d2 – диагонали, β – угол между ними.
4. Частный случай для ромба: S = 0,5 * (d1 * d2), где d1 и d2 – это диагонали ромба.

FAQ

Что понимается под параллелограммом?

Это плоская геометрическая фигура, противоположные стороны которое не только параллельны, но и имеют равную длину.

Каковы основные свойства фигуры?

У параллелограмма достаточно много отличительных свойств, включая несколько ключевых:

• равенство противоположных сторон;
• равенство противоположных углов;
• деление диагоналей пополам точкой пересечения;
• деление диагональю фигуры на два одинаковых треугольника;
• равенство суммы углов, прилегающих к одной стороне, 180 градусам;
• равенство суммы квадратов диагоналей удвоенной сумме квадратов непараллельных сторон фигуры.

Каковы главные признаки параллелограмма?

Параллелограммом является фигура, обладающая такими признаками:

1. Равенство и параллельность противолежащих сторон.
2. Попарное равенство противоположных сторон.
3. Разделение точкой пересечения каждой диагонали пополам.

Вывод

1. Параллелограмм – распространенная геометрическая фигура, частными случаями которой выступают ромб, квадрата и прямоугольник.
2. Ее изучают в 8 классе школьной программы.
3. Параллелограмм представляет собой четырехугольник, противолежащие стороны которого равны и параллельны.
4. Основные свойства фигуры: равенство противолежащих сторон и углов, разделение диагоналей точкой пересечения на равные части и т.д.