Осевая и центральная симметрия

Симметрия – это то, что мы можем наблюдать повсюду. Восприятие человека заставляет нас думать, что симметричные предметы являются красивыми. Поэтому законы симметрии особенно важны в работе архитекторов и дизайнеров. Рассмотрим, какие виды симметрии бывают и порешаем задачи для закрепления.

Симметрия – что это такое

Симметрией называется соразмерность, пропорциональность частей чего угодно, если они расположены по обе стороны от центра. Если говорить проще, то если рассматривать две части одного объекта относительно центра, и они являются одинаковыми, то это симметрия.

Осью симметрии фигуры называется прямая, которая позволяет разделить фигуру на две симметричные части. Взгляните на рисунки и вы поймете наглядно, что из себя представляет ось симметрии:

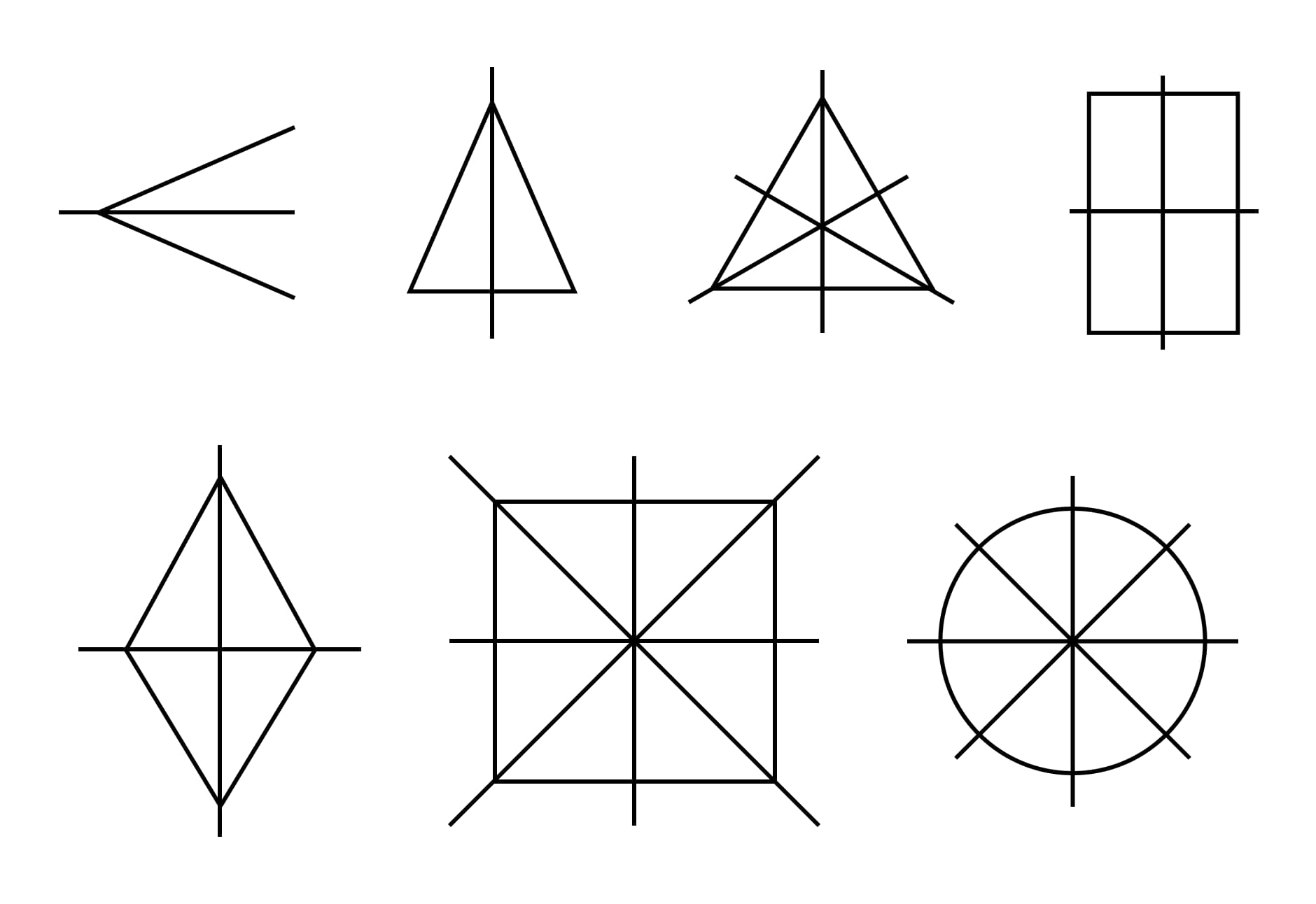
Центр симметрии – точка пересечения всех осей симметрии. На рисунке изображены симметричные фигуры с осями, которые представляют собой совершенно разные прямые:

• У угла осью симметрии является биссектриса, центра симметрии у него нет.
• У равностороннего треугольника осями симметрии являются биссектриса, медиана и высота, а точка их пересечения – центр симметрии.
• У прямоугольника оси симметрии проходят через середины его сторон.
• У ромба оси симметрии – прямые, которые содержатся в его диагонали.
• Квадрат имеет сразу 4 оси симметрии, так как он одновременно является прямоугольником и ромбом.
• У окружности бесконечно много осей симметрии. Если мы сказали сколько осей симметрии у квадрата, то назвать точное количество осей симметрии у окружности нельзя, так как в их роли могут выступать абсолютно любые прямые, которые были проведены через ее центр, центр окружности в этом случае и является центром симметрии.

Как мы уже говорили ранее, принято считать, что симметричные предметы считаются более красивыми. Хотя идеальная симметрия – это всегда рукотворные произведения, ведь в природе нет ничего абсолютно симметричного. Даже если взять нас с вами, и провести ось симметрии ровно по носу, то окажется, что наша правая часть не совсем похожа на левую. Отличаются как черты лица с разных сторон, так и длина ног (у 60% людей левая нога на 1-1,5 см длиннее правой).

Осевая симметрия

Осевая симметрия – представляет собой симметрию, которая проведена относительно прямой. При осевой симметрии у каждой точки, расположенной по одну сторону от прямой, всегда соответствует другая точка, которая расположена на второй стороне этой прямой. Если соединить симметричные точки, то полученный отрезок будет перпендикулярен оси симметрии.

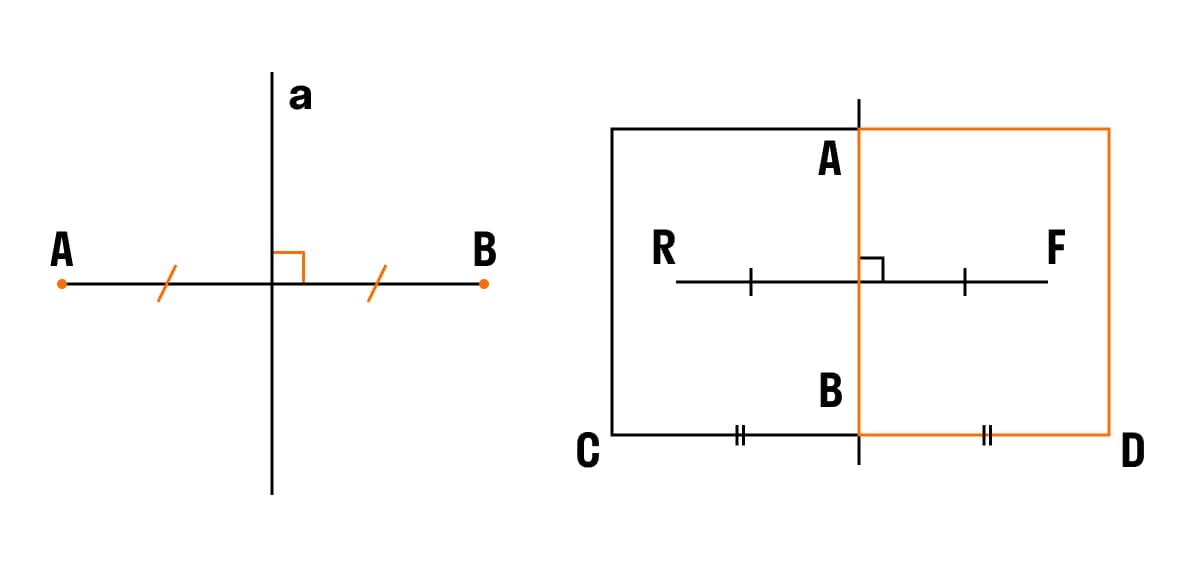
На представленных рисунках точки А и В являются симметричными относительно прямой а. Точки R и F являются симметричными относительно прямой АВ.

Осевая симметрия является неотъемлемой частью архитектуры, а в геометрии осевой симметрией обладают такие фигуры, как квадрат, треугольник, ромб, прямоугольник. Однако существуют фигуры, которые не имеют осей симметрии, например, параллелограмм и разносторонний треугольник.

Обратите внимание, что симметричные относительно прямой фигуры являются равными.

Центральная симметрия

Центральной симметрией является симметрия относительно точки.

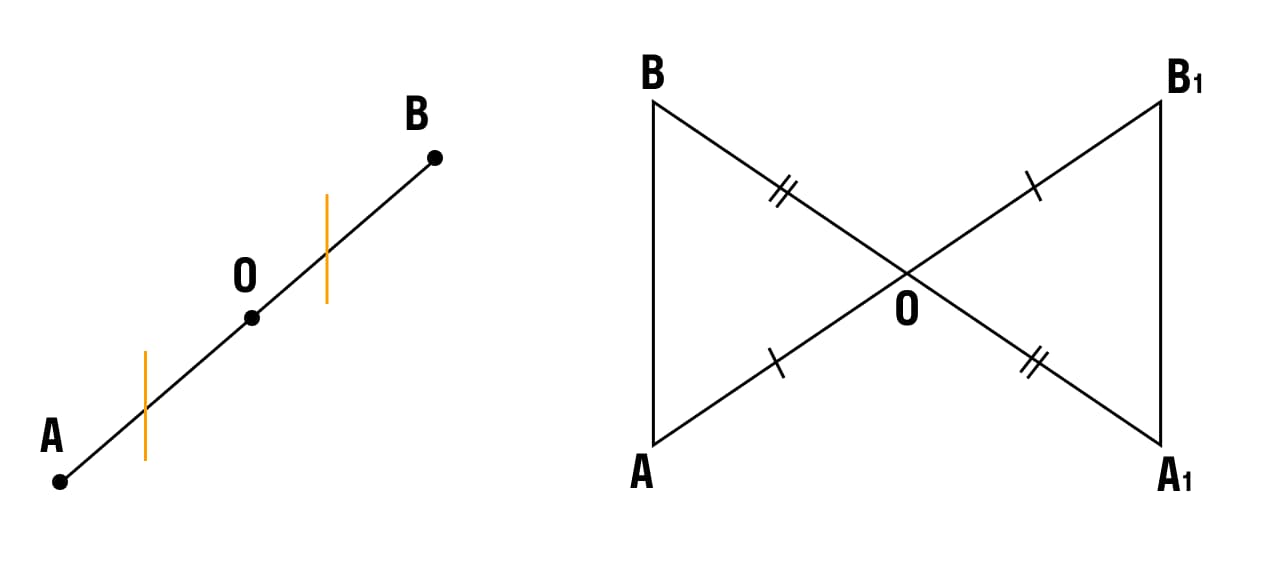
На представленных рисунках точка 0 является центром симметрии.

Примеры – задачи и решение

Часто при решении геометрических задач требуется построить симметричные фигуры. Рассмотрим принципы построения фигур, которые будут симметричны данной относительно прямой и точки.

Задача 1: Постройте треугольник A₁B₁C₁, который будет симметричным треугольнику АВС относительно прямой.

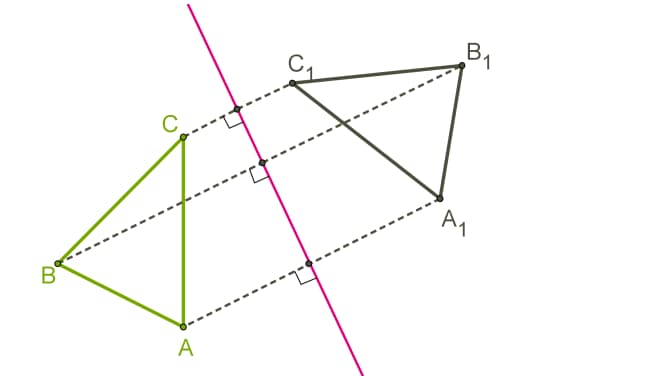
Для построения такого треугольника необходимо:

1. Провести из вершин прямоугольника АВС прямые, которые будут перпендикулярны оси симметрии (в соответствии с особенностями осевой симметрии).
2. Измерить расстояние от вершин треугольника до получившихся на прямой точек.
3. Отложить с другой стороны прямой такие же расстояния.
4. Соединить получившиеся точки отрезками.

Задача 2: постройте центрально-симметричный треугольник A₁B₁C₁ с центром симметрии в точке О.

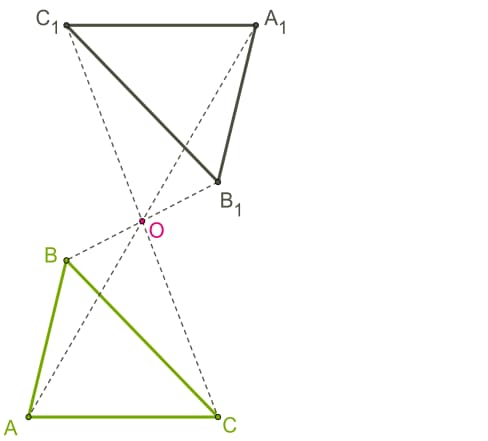
Для построения треугольника A₁B₁C₁, который будет симметричным треугольнику АВС относительно точки О необходимо:

1. Соединить вершины А, В, С и центр прямыми.
2. Измерить отрезки АО, ВО, СО.
3. Отложить с другой стороны от точки О равные отрезки, лежащие на соответствующих прямых.
4. Соединить получившиеся точки отрезками.

В результате мы получим треугольник A₁B₁C₁, который является симметричным данному треугольнику АВС.

FAQ

Являются ли симметричные фигуры равными?

Да, фигуры, которые симметричны относительно некоторой точки или прямой являются равными.

Все ли фигуры имеют центральную симметрию?

Нет, есть большой перечень фигур, которые не являются симметричными, например, разносторонний треугольник, параллелограмм.

Чем отличается осевая симметрия от центральной?

Центральная симметрия – это симметрия относительно одной точки, а осевая – относительно прямой.

Сколько осей симметрии у квадрата?

Квадрат совмещает в себе оси симметрии ромба и прямоугольника, поэтому у него 4 оси симметрии.

Заключение

Симметрия окружает нас повсюду, она считается показателем красоты. Абсолютную симметрию в природе встретить невозможно, да, если говорить, например, о бабочке, то она может показаться нам относительно симметричной по осевой симметрии, но это не так. Абсолютная симметрия – это всегда что-то рукотворное, то, к чему стремится человек, например, в архитектуре. Принципы построения симметричных фигур относительно оси и центра позволяют решать различные геометрические задачи, будут полезны на экзаменах.