Область определения функции

Область определения функции представляет собой множество, на котором задаётся функция. Чтобы найти совокупность значений, которые могут быть использованы в качестве входных данных, необходимо понимать элементарные правила математических операций с числами.

Область определение функции – понятие

Область определения функции – это множество значений её аргумента (независимой переменной) или, иными словами, набор принимаемых ей входных значений. Геометрически она представляет собой проекцию графика функции на ось абсцисс (горизонтальную ось 0x).

Если задана некоторая функция ƒ, отображающая множество X во множество Y (записывается как ƒ: X → Y), то X называют областью определения функции. Её принято обозначать как D(ƒ).

Области определения основных элементарных функций

Каждая функция имеет свою область определения, которое рассматривается как её свойство. А если выразиться точнее, то она не существует без этой составляющей.

Рассмотрим области определения основных элементарных функций.

Область определения линейной функции

Линейной называют такую функцию, которая показывает прямую линию на координатной плоскости. В общем случае она выражается формулой y = kx + b, где k (угловой коэффициент), b (свободный коэффициент) – некоторые числа, x – независимая переменная, y – зависимая переменная.

Например, задана линейная функция y = 3x + 5, или ƒ(x) = 3x + 5, где ƒ: X → Y. Выберем 2 произвольные точки x₁= -1 и x₂ = 0 и подставим в уравнение; рассчитаем соответствующие значения y₁ = 2, y₂ = 5. Нанесём точки с координатами (-1, 2) и (0, 5) на координатную плоскость и проведём через них прямую линию – получится график линейной функции.

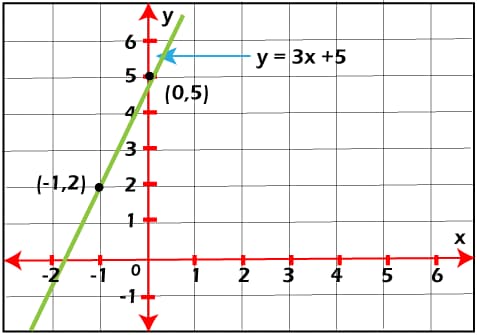
Очевидно, что линейная функция принимает любые аргументы. Её область определения представлена множеством действительных чисел: D(ƒ): x ∈ R, или D(ƒ) = (−∞, +∞).

Область определения постоянной функции

Постоянной называют такую функцию, которая всегда принимает одно и то же выходное значение независимо от того, какое числовое значение передаёт аргумент. В общем случае она задаётся формулой y = N, или ƒ(x) = n, где n – это любое из множества R действительных чисел. Таким образом, она не имеет переменных и является константой – постоянной величиной.

Постоянная функция является частным случаем линейной функции. Поэтому ƒ(x) = n может быть записана как y = kx + n, где k – угловой коэффициент, n – свободный коэффициент. Например, если задана постоянная функция y = 3, или ƒ(x) = 3, где ƒ: R → R, то она принимает форму y = 0x + 3 и графически изображается так:

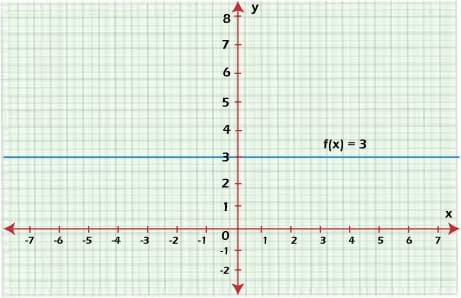
Здесь показано, что областью определения постоянной функции является множество R действительных чисел: D(ƒ): x ∈ R, или D(ƒ) = (−∞, +∞).

Область определения степенной функции

Степенной называют функцию, выраженную уравнением с целыми показателями степени. В общем случае она представлена формулой ƒ(x) = xⁿ, где n – это любое действительное число, x – переменный показатель в основании степени. Например, ƒ(x) = x⁵ – это функция степени 5 по основанию x.

Область определения степенной функции ƒ(x) = xⁿ находится в прямой зависимости от показателя степени n. Возможно несколько вариантов:

• если n – это неотрицательное число, то область определения функции представлена множеством любых действительных чисел, или D(xⁿ) = (−∞, +∞);
• если n – это нецелое число, то аргумент принимает только положительные значения; тогда область определения – это множество неотрицательных действительных чисел, или D(xⁿ) = [0, +∞);
• если n – это отрицательное число или ноль, то область определения функции представлена множеством действительных чисел, отличных от нуля, или D(xⁿ) = (−∞, 0) ∪ (0, +∞).

Область определения корневой функции

Корневой называют подтип степенной функции, которая в общем случае выражается формулой ƒ(x) = x^1/n, где n – это целое положительное (больше нуля) число. Например, ƒ(x) = x^1/2= √x – функция квадратного корня, а ƒ(x) = x^1/3= ³√x – функция кубического корня.

Область определения корневой функции находится в прямой зависимости от чётности и нечётности показателя n. Следовательно, возможны такие варианты:

• если n – это положительное чётное целое число (что удобно записать как n = 2m, где m ∈ N), то её область определения – это множество неотрицательных действительных чисел, или D(^2m√x) = [0, +∞);
• если n – это положительное нечётное число (что удобно записать как n = 2m+1, где m ∈ N), то её область определения – это множество действительных чисел, или D(^2m+1√x) = (−∞, +∞).

Область определения показательной функции

Показательной называют функцию возведения постоянной константы в степень переменной. В общем случае она выражается формулой ƒ(x) = a^x, где a – это неотрицательное (и не равное 1) вещественное число, а x – показатель степени. Функции подобного типа используются при описании свойств несложных динамических систем; в качестве примера можно привести:

• y = 100^x;
• y = (√25)^x;
• y = e^x – экспонента (вещественная или комплексная);
• m = m₀*2^-t/T – формула, описывающая закон радиоактивного распада;
• n = n₀*e^at – формула, описывающая рост народонаселения.

Показательная функция принимает любые аргументы; её область определения – это множество действительных чисел: D(ƒ): x ∈ R, или D(ƒ) = (−∞, +∞).

Область определения логарифмической функции

Логарифмической называют функцию, обратную показательной. В общем случае она выражается формулой ƒ(x) = log_ax при условии, что a>0 и a≠1. Логарифмические функции могут включать натуральный (ln) или десятичный (log) логарифмы; в качестве примера можно привести:

• ƒ(x) = log₅x;
• ƒ(x) = log _√25x;
• ƒ(x) = ln(x - 2);
• ƒ(x) = log₂(x + 5) – 2;
• ƒ(x) = 2log

Область определения логарифмической функции представлена множеством положительных действительных чисел: D(ƒ): x ∈ R, или D(ƒ) = (−∞, +∞).

Область определения тригонометрических функций

Тригонометрическими называют элементарные функции, которые выражают зависимости между сторонами и острыми углами прямоугольных треугольников. Основные из них представлены формулами:

• ƒ(x) = sin x – функция синуса;
• ƒ(x) = cos x – функция косинуса;
• ƒ(x) = tg x – функция тангенса;
• ƒ(x) = ctg x – функция котангенса.

Область определения тригонометрических функций синуса и косинуса – это множество действительных чисел: D(ƒ): x ∈ R, или D(ƒ) = (−∞, +∞). Однако если x является аргументом функций тангенса и котангенса, то их области определения представлены математическими множествами всех действительных чисел, но при условии, что x ≠ π/2+ πk, k ∈ z (для тангенса) и x ≠ πk, k ∈ z (для котангенса).

FAQ

Как найти область определения функции?

Чтобы найти область определения (в рамках последовательности действительных чисел), нужно понять, к какому типу относится функция; затем из спектра возможных значений аргумента устранить неподходящие интервалы. Чтобы установить исключения, нужно учитывать несколько аспектов:

• нельзя разделить число на ноль;
• нельзя извлечь корень чётной степени из отрицательного числа;
• нельзя логарифмировать отрицательное число;
• нельзя найти арксинус или арккосинус числа, которое больше 1 и меньше -1.

Например, задана функция ƒ(x) = √(x² - 1), где x принадлежит множеству действительных значений. Поскольку невозможно извлечь корень чётной степени из отрицательного числа, то мы понимаем, что x² - 1 ≥ 0. Соответственно, из области определения функции будут исключены все значения x² - 1 < 0.

Используя метод интервалов, находим корни неравенства: x² - 1 = (x - 1)(x + 1) = (x - 1)(x - (-1)) → x₁ = 1; x₂ = -1. Отмечаем их на координатной оси прямой. И, поочерёдно подставляя значения из различных интервалов, выясняем, что неравенство x² - 1 < 0 соблюдается на отрезке (-1, 1).

Таким образом, область определения функции ƒ(x) = √(x² - 1) является множеством, полученным путём объединения 2 интервалов: D(ƒ) = (-∞, -1] ∪ [1, +∞).

Как правильно обозначать область определения функции?

Область определения функции обозначается как D(y), или D(ƒ). При этом множество значений обычно указывается в скобках: записывается начальное и конечное значение интервала. Например, если задана функция y = x^2/3, то её область определения записывается как D(ƒ) = [0, +∞).

Обратите внимание, что в записи используются квадратные и круглые скобки. Первые ставятся в случае, если граничное число входит во множество, вторые – если не входит.

Вывод

Часто школьникам сложно сразу понять, как находить область определения функции. Чтобы быстро и качественно освоить эту тему, в первую очередь следует изучить типы функций. По расположению аргумента в уравнении всегда можно понять, какие математические операции можно или нельзя совершать, и, в конечном итоге, выявить область определения.