Область допустимых значений

Что такое область допустимых значений

Область допустимых значений функции - это множество всех значений независимой переменной, при которых функция определена. Она определяется ограничениями на значения переменных, которые могут вводиться в функцию без приведения к неопределенности или недопустимости.

Как ее найти

Рассмотрим это на примере функции 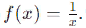 В данном случае, область допустимых значений функции f(x) - это все значения x, кроме нуля, так как деление на ноль является недопустимой операцией. Таким образом, область допустимых значений функции f(x) можно записать как ∈(−∞,0)∪(0,+∞), где символ ∪ обозначает объединение множеств.

В других функциях область допустимых значений может быть определена другими ограничениями, например, в радикальной функции 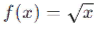 областью допустимых значений будет множество всех неотрицательных действительных чисел, так как радикал из отрицательного числа не определен в действительных числах.

Пример решений

Давайте рассмотрим пример функции и найдем её область допустимых значений.

Пусть дана функция 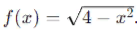 Чтобы найти область допустимых значений этой функции, нужно найти значения x, при которых аргумент под корнем неотрицателен, так как извлечение корня из отрицательного числа не определено в области действительных чисел.

Итак, условие для того, чтобы аргумент под корнем 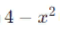 был неотрицателен, это:

4 − 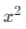 ≥0

Это неравенство можно решить, используя методы алгебры:

4 ≥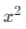

Теперь избавимся от знака неравенства, взяв корень из обеих частей:

2 ≥∣x∣

Таким образом, мы получаем, что ∣x∣≤2. Это означает, что x находится в пределах от -2 до 2 включительно.

Таким образом, область допустимых значений функции 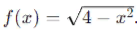 - это все действительные числа x, такие что −2 ≤ x ≤ 2.

Иногда область допустимых значений может быть ограничена не только самой функцией, но и контекстом задачи или математической модели, в которой она используется.