Неполные квадратные уравнения

Многие из тем, которые школьники проходят в 8 классе, встречаются на ЕГЭ. Одной из них являются неполные квадратные уравнения и их решения. Поэтому на этот раздел алгебры стоит обратить особое внимание.

Неполные квадратные уравнения – что это

Уравнением в математике называют равенство с неизвестными. Неизвестное может быть одно или несколько. Решив уравнение, мы получаем значение неизвестного, подставив которое в уравнение, получим правильное числовое равенство.

Если неизвестное стоит во второй степени, такое уравнение называют квадратным. Оно имеет вид: ах²+bх+с=0, где а является первым коэффициентом, b – вторым коэффициентом, а с – свободным членом.

Сколько корней будет иметь уравнение? Это зависит от дискриминанты. Для ее расчета, используют формулу: D=b²-4ас. Свойства дискриминанта следующие:

• если значение D меньше нуля, то корней у такого уравнения нет;
• если D=0, то корень всего один;
• если значение D больше нуля, то у уравнения будет 2 корня.

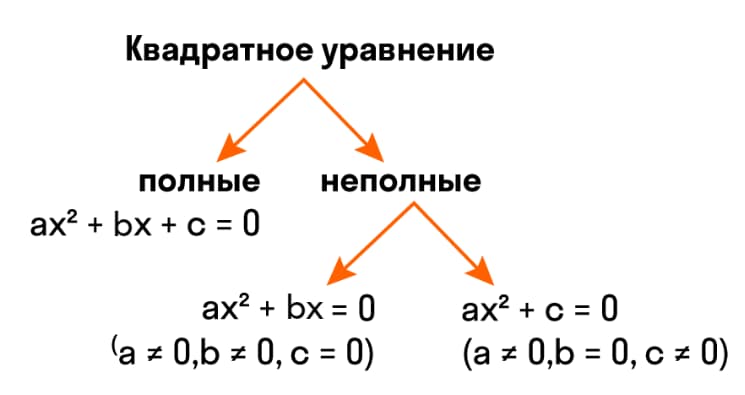
Неполным называют квадратное уравнение вида ах²+bх+с=0, в котором хотя бы один из коэффициентов b или с равны нулю.

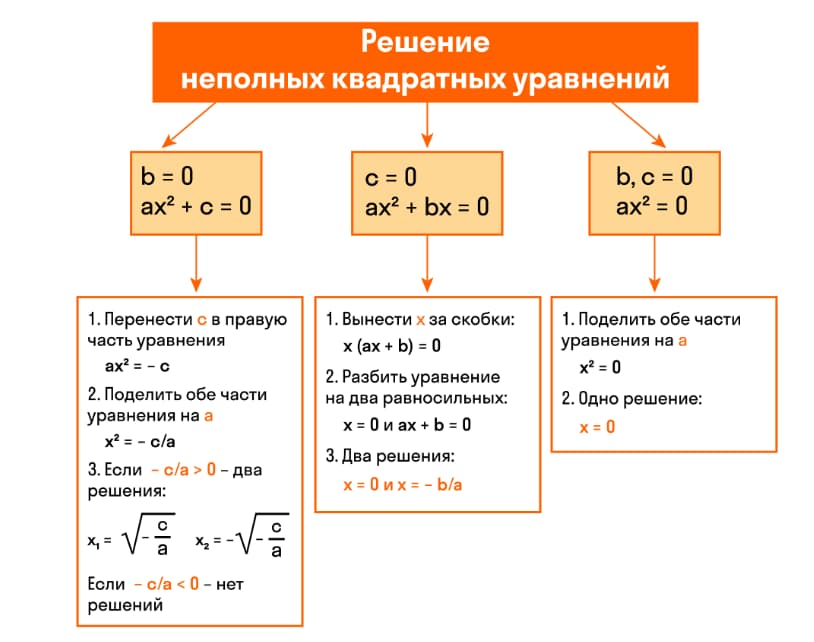
Как решать неполные квадратные уравнения

Известно три вида неполных квадратных уравнений:

• ах²=0, у которого коэффициенты b=0 и с=0;
• ах²+с =0 при b=0;
• ах²+bх+с=0, где с=0.

Решение уравнений ах²=0

ах²=0 это то же самое, что х²=0. Это мы получаем, разделив обе части равенства на число а, не равное нулю. Корнем уравнения х²=0 будет нуль 0²=0. Исходя из свойств степеней, других корней у такого уравнения нет.

Поэтому единственным корнем уравнения вида ах²=0 будет х=0.

Блок-схема решения уравнений вида ах²=0 выглядит так:

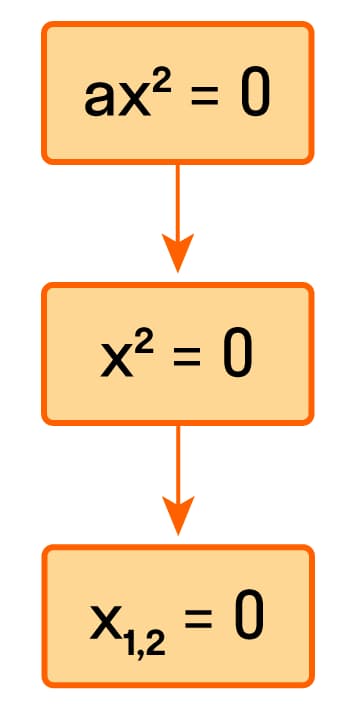
Например, решим уравнение -5х²=0

х²=0

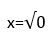
х=0

Ответ: 0.

Решение уравнения ах²+с =0

Как решить уравнение ах²+с =0, где b равен нулю и с не равен нулю. Мы знаем, что при переносе слагаемого из одной части уравнение в другую, оно меняет знак на противоположный. Также известно, что если обе части уравнения разделить на одно и то же самое число (за исключением нуля), то получим равносильное уравнение, но уже с другими цифрами.

Поэтому решаем уравнение ах²+с =0 следующим образом:

• переносим значение с в правую часть равенства, получаем ах² =-с;
• разделим обе части равенства на а, получаем х² =-с/а.

Исходя из того, какие значения имеют а и с, выражение с/а может быть положительным или отрицательным:

1. Если –с/а меньше нуля, то у уравнения х² =-с/а корней не будет, так как квадрат любого числа всегда является положительным числом.
2. Если –с/а больше нуля, то корни такого уравнения будут другими. К примеру, здесь можно использовать правило квадратного корня. В таком случае получим корень, равный числу 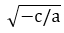 потому что 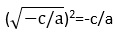. Также корнем может быть 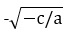, потому что .

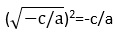Блок-схема решения уравнения ах²+с = 0 будет следующей:

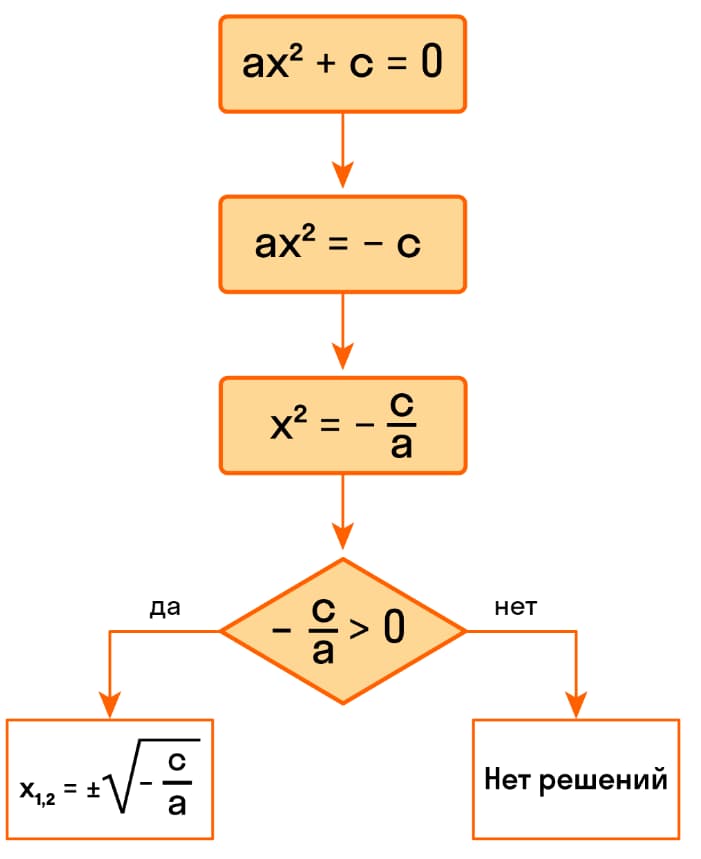
К примеру, решим уравнение 9х²+4=0:

1. Переносим свободный член в правую часть равенства:

   9х²=-4

2. Делим обе части на 9:

   х²=-4/9

3. В правой части получаем отрицательное значение, значит у данного уравнения нет корней.

Решим уравнение –х²+9=0

1. Переносим свободный член в правую часть равенства:

   х²=-9

2. Делим обе части на -1:

   
   

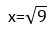
   х=-3,3.

   У данного уравнения 2 корня - -3 и 3.

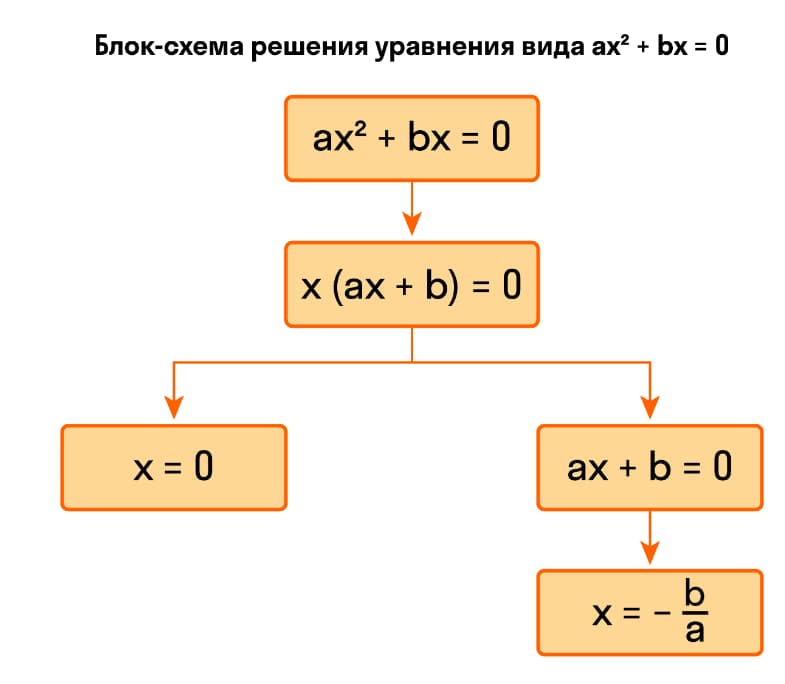
Решение уравнения ах²+bх+с=0

Такое уравнение можно решать способом разложения на множители. Для этого выносим за скобки общий множитель х. Получаем равносильное уравнение х*(ах+b)=0, что равносильно совокупности уравнений х=0 и ах+b=0. У второго линейного уравнения корень х=-b/а. Отсюда имеем 2 корня уравнения:

• х=0;
• х=-b/а.

В качестве примера решим уравнение 2х²-32х=0.

1. Выносим общий множитель х за скобки. х(2x - 32) = 0
2. Это уравнение равносильно х=0 и 2х-32=0.
3. Остается решить линейное уравнение:

   2х=32

   х=32/2

   х=16.

   Получаем корни уравнения 0 и 16.

   Решим еще одно уравнение 3х²-12х=0

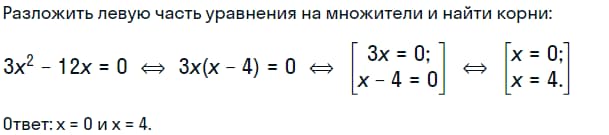
Задачи для самопроверки

Онлайн-калькуляторы – обзор решений

Чтобы проверить правильность решения неполных квадратных уравнений, можно воспользоваться он-лайн калькуляторами:

1. OnlineMSchool – простой в использовании онлайн-калькулятор, позволяющий быстро найти корни квадратного уравнения.
2. ecalc – решение квадратных уравнений при помощи специальных формул, через дискриминант и теорему Виета.
3. SmartCalculator.online – вычислит любой тип квадратного уравнения.

FAQ

Что такое приведенное квадратное уравнение?

Приведенное квадратное уравнение – это полное квадратное уравнение, где коэффициент а=1.

Как звучит теорема Виета?

Корни приведенного квадратного уравнения х²+рх+q=0 в сумме дают –р, а их произведение равно q.

Вывод

Неполное квадратное уравнение может иметь 3 вида для каждого из которых есть свои решения. Освоив их, можно будет легко решить любой пример из данной темы.