Натуральные числа
Натуральными числами называются те числа, которые мы используем чтобы подсчитать что-то конкретное, осязаемое. Наименьшим натуральным числом является единица (1), а вот наибольшего натурального существа не существует – натуральный ряд является бесконечным. Каждое последующее натуральное число больше предыдущего на единицу. Рассмотрим особенности, свойства натуральных чисел, разберем задачи и решения с ними.
Определение натурального числа – что это
Натуральные числа (от лат. naturalis «естественный) – это те числа, которые возникают естественным способом при подсчете. Последовательность всех натуральных чисел, которые расположены в порядке возрастания называют натуральным рядом. Бесконечность множества натуральных чисел связана с тем, что для любого натурального числа n найдется число n+1.
Первые сто натуральных чисел вы можете посмотреть в таблице натуральных чисел:
Множество всех натуральных чисел принято обозначать латинской буквой N.
С натуральными числами можно проводить такие операции, как:
- сложение;
- умножение;
- вычитание, однако, стоит отметить, что уменьшаемое число при вычитании должно быть строго больше вычитаемого, иначе в результате получится число, которое не входит в ряд натуральных чисел (0 или отрицательное).
- деление;
- деление с остатком;
- возведение в степень.
Десятичная запись натурального числа
С понятием натуральных чисел школьники сталкиваются в 5 классе, однако многое из этой темы понятно намного раньше. При записи любого натурального числа мы используем цифры от 0 до 9. При этом натуральные числа могут записываться только с использованием цифр, без дополнительных символов.
При написании натуральных чисел необходимо записывать цифры одну за другой слева на право в строчку. При этом цифры должны быть одной высоты.
Если написать последовательность чисел, например, 00237, то она не может считаться натуральным числом, так как ноль расположен с лева, а натуральное число не может начинаться с нуля. Это и есть десятичная запись натурального числа.
Количественный смысл натуральных чисел
Натуральные числа используются для нумерации любых предметов. Они несут в себе количественный смысл. Представим, что перед нами лежит яблоко. Мы можем записать, что видим 1 яблоко. Любое количество яблок можно начать считать и записывать их с помощью натуральных чисел. Именно указание количества предметов является основной функцией натурального числа.
Если предметов нет, то запись такого числа совпадает с цифрой 0. Однако ноль не является натуральным числом, оно может лишь обозначать отсутствие чего-либо. Ноль яблок – значит ни одного яблока.
Однозначные, двузначные, трехзначные натуральные числа
Однозначными натуральными числами называются те, в составе которых входит только один знак (цифра). Всего существует 9 натуральных чисел – от 1 до 9.
Двузначными натуральными числами называются те, в записи которых содержится две цифры. При этом они могут повторяться или быть различными, например: 13, 97.
По своей сути двузначные числа являются набором однозначных, в котором одно записывается с левой стороны, другое – с правой. Левые числа указывают на количество десятков, а правые – на количество единиц. Двузначных натуральных чисел 90: от 10 до 99.
Трехзначные натуральные числа строятся по тому же принципу, что и двузначные. Однако в них уже три цифры. Левая указывает на количество сотен, средняя – на десятки, а правая – на единицы.
С помощью цифры 0 в записи двузначных или трехзначных натуральных чисел указывается на отсутствие одного единиц. В трехзначных числах 0 может использоваться и для демонстрации отсутствия десятков.
Подобные же определения имеют четырехзначные, пятизначные, десятизначные и другие натуральные числа.
Многозначные натуральные числа
Многозначными натуральными числами называются те, что состоят из двух и более знаков. Другими словами, двузначные натуральные числа уже являются многозначными.
1 000 можно представить в виде множества из 10 сотен, а 1 000 000 – это тысяча тысяч. Любое натуральное число можно рассмотреть, как набор однозначных натуральных чисел. Например, число 2 313 220 содержит в себе: 0 единиц, 2 десятка, 2 сотни, 3 тысячи, 1 десятка тысяч, 3 сотен тысяч и 2 миллионов.
Свойства натуральных чисел
Подробно рассмотрим свойства натуральных чисел, с которыми вы можете познакомиться в таблице ниже:
|
множество натуральных чисел |
начинается с единицы (1) и является бесконечным |
|
за каждым натуральным числом идет следующее |
следующее число больше предыдущего на 1 |
|
деление натурального числа на единицу (1) |
результатом является само натуральное число: 10:1=10 |
|
деление натурального числа самого на себя |
результатом деления является единица (1): 10:10=1 |
|
переместительный закон сложения |
от перестановки мест слагаемых сумма не меняется: 10+1=1+10 |
|
сочетательный закон сложения |
результат сложения нескольких слагаемых не меняется от порядка выполненных действий: (10+1)+8=10+(1+8) |
|
переместительный закон умножения |
от перестановки мест множителей произведение не меняется: 3х4=4х3 |
|
сочетательный закон умножения |
результат произведения множителей не зависит от порядка действий: (2 х 3) х 4=2 х (3 х 4) |
|
распределительный закон умножения относительно сложения |
для умножения суммы на число, можно каждое слагаемое умножить на число и сложить полученный результат: 4 х (3+5) = 4 х 3 + 4 х 5 |
|
распределительный закон умножения относительно вычитания |
для умножения разности на число, можно умножить на это число уменьшаемое и вычитаемое, а затем из первого произведения вычесть второе: 4 х (5-3) = 4 х 5 - 4 х 3 |
|
распределительный закон деления относительно сложения |
для деления суммы на число, можно разделить на это число каждое слагаемое, а потом сложить полученные результаты: (4+5):3=4:3+5:3 |
|
распределительный закон деления относительно вычитания |
для деления разности на число, можно разделить на это число отдельно уменьшаемое, а затем вычитаемое, и из первого произведения вычесть второе: (5-4):3=5:3-4:3 |
Разряды натурального числа
В зависимости от позиции, на которой стоит цифра, записанная в числе, зависит ее значение. Так, в числе 981 содержится 1 единица, 8 десятков и 9 сотен. Можно это сформулировать иначе: цифра 9 располагается в разряде единиц, 8 – в разряде десятков, и 9 – в разряде сотен.
Разрядом называется позиция цифры, которую она занимает в записи натурального числа.
Каждый разряд имеет свое название, которое вы можете посмотреть в таблицы. В левой части располагаются старшие разряды, справа – младшие:
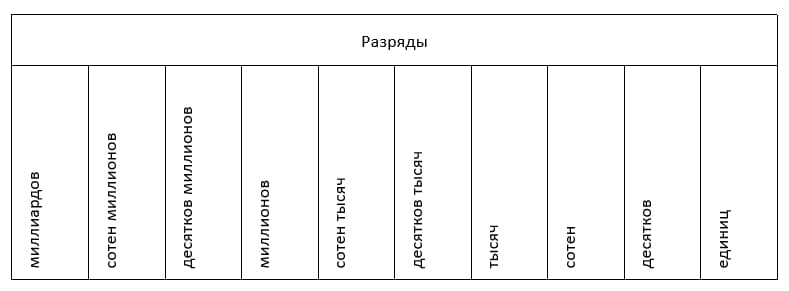
Количество знаков в числе соответствует количеству разрядов. В таблице представлены названия разрядов для чисел, состоящих из 10 знаков. У следующих разрядов есть свои названия, но их не так часто используют.
Младшим или низким разрядом многозначного числа называется разряд единиц.
Высший или старший разряд многозначного натурального числа – разряд, который соответствует самой левой цифре в числе.
В учебниках часто ставят пробелы во время записи многозначных чисел. Это делается для того, чтобы было удобнее считать. Кроме того, с помощью пробелов выделяются разные классы чисел.
Классом являются группа разрядов, которая содержит в себе три разряда: единиц, десятков и сотен.
Например, в числе 348 257 представлено 6 разрядов и 2 класса:
- класс единиц, в который входят 7 единиц, 5 десятков, 2 сотни;
- классы тысяч, в который входят 8 тысяч, 4 десятка тысяч, 3 сотни тысяч.
Подобное актуально и для класса, миллионов, миллиардов и т.д.
Десятичная система счисления
С течением времени люди использовали разные записи чисел. Используемые системы счисления имеют свои правила и особенности. Самой распространенной системой счисления является десятичная. В ней для записи чисел используются десять знаков: от 0 до 9.
В десятичной системе исчисления значение одной и той же цифры напрямую зависит от ее позиции в числе. Допустим, число 2 222 состоит из 4 одинаковых цифр. При этом первая обозначает 2 тысячи, вторая – 2 сотни, третья 2 десятка, а последняя – 2 единицы. В связи с тем, что значение цифры напрямую зависит от ее позиции при записи, десятичная система счисления так же называется позиционной.
Разберем примеры – задачи и решение
Для закрепления материалов, решим несколько примеров.
Задача 1.
Даны числа: 15, 353, 905, 15 357, 7 252 100. Что означает цифра 5 в каждом из записанных чисел?
Ответ:
- 15 – единицы.
- 353 – десятки.
- 905 – единицы.
- 15 357 – десятки.
- 7 252 100 – десятки тысяч.
Задача 2.
Запишите число 35 столько раз, сколько указано в задании и прочитайте получившиеся числа:
- Два раза;
- Три раза;
- Пять раз.
Ответ:
- 3 535 – три тысячи пятьсот тридцать пять;
- 353 535 – триста пятьдесят три тысячи пятьсот тридцать пять;
- 3 535 353 535 – три миллиарда пятьсот тридцать пять миллионов триста пятьдесят три тысячи тридцать пять.
Задача 3.
Сколько цифр содержится в числе 5 875 578 857, перечислите эти цифры.
Ответ:
Число содержит только 3 цифры: 5, 7 и 8.
FAQ
Сколько всего натуральных чисел?
Количество натуральных чисел является бесконечным.
Какое самое маленькое натуральное число?
Самым маленьким натуральным числом является единица.
Являются ли отрицательные числа натуральными?
Нет, натуральные числа – это только те числа, с помощью которых мы можем посчитать объекты. Поэтому они начинаются с 1.
Заключение
Натуральные числа мы используем повседневно для определения количества каких-либо предметов. Они состоят из цифр от 0 до 9, но весь ряд натуральных чисел начинается с единицы (1). Конечно, в математике существуют и другие варианты записи различных значений, например, дробные числа и т.д., но они не так часто используются в реальной жизни.
