Нахождение наибольшего и наименьшего значения функции

Ученикам и некоторым учителям не нравится раздел в алгебре, который посвящен нахождению наибольшего и наименьшего значения функции. Однако решение позволяет открыть дорогу в углубленное изучение математики и математического анализа, без которых не может существовать современная IT-индустрия.

Поэтому, если вы хорошо поймете алгоритмы нахождения наибольшего и наименьшего значения функции, то дальнейшее изучение алгебры вам покажется простым и легким.

Функция – что это такое

В первую очередь давайте познакомимся с тем, что представляет собой функция. Узнаем ее значение, дадим ей определение.

В нашем мире каждая частица зависит от другой похожей или непохожей частицы. То есть мир представляет собой огромное количество взаимосвязей. Например, температура может влиять на течение определенных физиологических процессов. Чтобы вычислить эти взаимосвязи используют специальные формулы. Эти формулы позволяют проводить вычисления в два раза быстрее.

Отсюда даем определение функции. Функция — это формула или математическое выражение, описывающая связь взаимосвязей двух величин, тел.

Например, давайте попробуем вычислить взаимосвязь пройденного пути и времени. В алгебре эту взаимосвязь обозначают следующей формулой: S(t) = Vt.

Давайте узнаем есть ли формула взаимосвязи для нахождения ускорения тела от силы, приложенной к этому телу. Такая взаимосвязь выражается в следующей формуле: F = ma.

В подобных формулах обязательно присутствуют две переменные:

• зависимая;
• независимая.

Зависимая — это та, которую определяют. Она и является функцией. А независимая переменная является аргумент. Зависимая переменная всегда ставится слева от знака «=»

Графическое задание функции

Каждая функция имеет свое графическое задание. Это график, который наглядно показывает взаимосвязь двух переменных: зависимой и независимой. Такие графические задания нужны для более плотного понимания того, что решает функция.

Давайте представим, вы выступаете на конференции, посвященной защите животных из красной книги. Вы оперируете числами, рассказываете о том, как уменьшается или увеличивается то или иное поголовье животных в устной форме. Как думаете, многим устное изложение будет интересно и много ли людей запомнят цифры из вашего доклада? Конечно, нет. Некоторые даже уснут во время лекции.

Однако если вы все цифры представьте и покажите на графиках, то сможете заинтересовать аудиторию. Так и в алгебре для лучшего понимания функций чертят график в системе координат.

Внимание! График — это прямая, кривая или ломаная линия, которую чертят в системе координат в строгом соответствии с числами, указанными в функции.

Для примера, посмотрите на скрине ниже показаны графики с различными взаимосвязями зависимой и независимой переменных в системе координат.

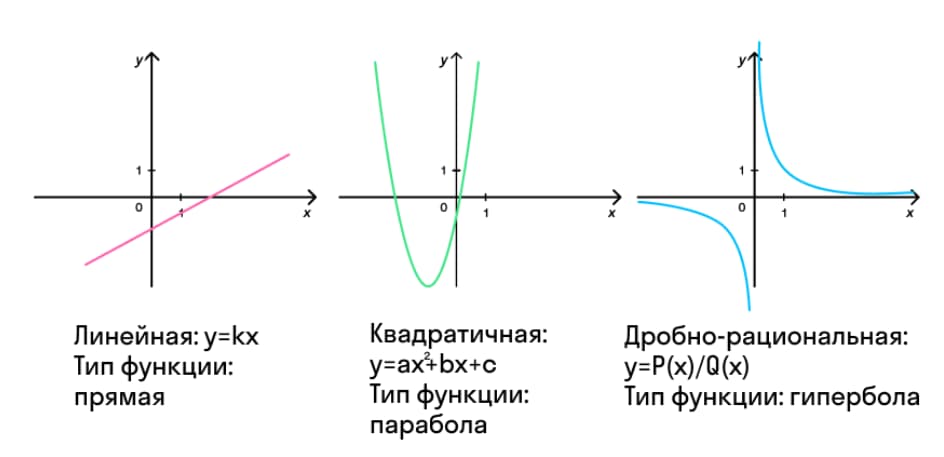
Наибольшее и наименьшее значение функции

Теперь, когда мы уже знаем, что такое функция, как отобразить ее на графике в системе координат, давайте попробуем определить наибольшее и наименьшее значение функции. Вас об этом может попросить учитель на уроке алгебры или же может попасться такой вопрос в билете на экзамене.

Наибольшее значение функции называют максимальным и отображают в виде сокращения от латинского «maximum» — max. Наименьшее значение функции называют минимальным и отображают в формуле в виде сокращения от латинского слова «minimum» — min.

Теперь давайте возьмем функцию и отобразим ее в виде формулы: y = f(x). Нам нужно найти наибольшее значение функции или ее максимум. Отобразим формулу следующим образом:

• max y = f(x0).

Наибольшее значение функции – это ее наибольшее число, которое она может принимать на известном интервале при абсциссе x0.

Находим наименьшее значение функции

Теперь давайте пропишем формулу, чтобы найти минимальное значение функции. Для этого используем сокращение «min»:

• min y = f(x0).

Наименьшее значение функции — это самое маленькое принимаемое значение на том же интервале при x0.

Мы уже знаем, что «x» — это некоторый промежуток.

При нахождении наибольшего и наименьшего значения функций мы должны знать и стационарные точки. Ими называются такие значения аргумента функции, при которых производная превращается в ноль. Однако речь о производной будет идти в специальном блоке ниже. Пока что давайте посмотрим, как максимальные и минимальные значения функции будут выглядеть на графиках.

Наибольшее и наименьшее значение функции на графиках

Вы изучили формулы функций, знаете, как находить наибольшее и наименьшее значения. Давайте теперь попробуем эти значения отобразить на графиках.

Пусть интервал функции будет представлен прямой. Если изобразить функцию на графике в виде прямой возрастающей функции, то наименьшее значение такая функция примет при наименьшем аргументе. То есть аргумент будет находится в нижней точке системы координат. А наибольшее значение аргумента будет соответствовать наибольшему значению на графике функции.

На скрине изображена возрастающая функция в виде прямой.

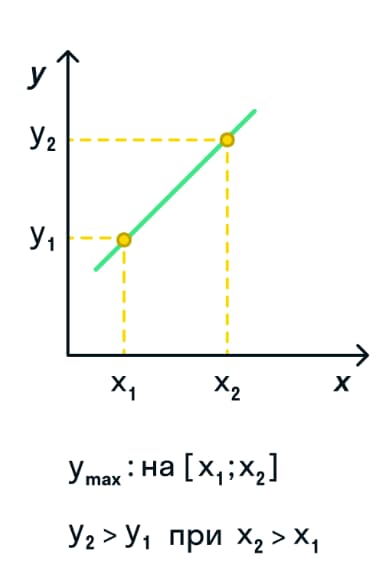
Если функция убывает, то наименьшее значение функция примет при наибольшем аргументе и наибольшее значение функции будет соответствовать наименьшему значению аргумента. На скрине эта зависимость четко отображена.

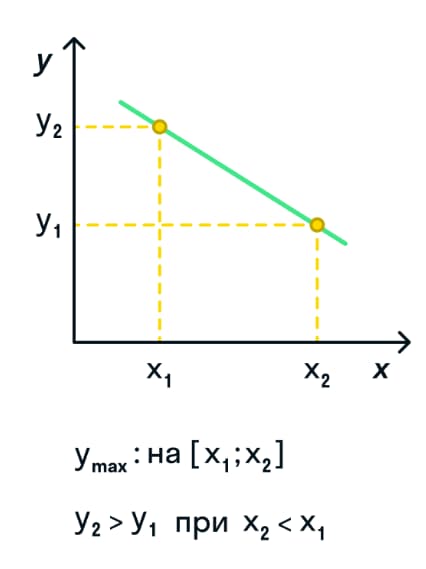
Бывает так, что интервал функции задается в виде кривой. Давайте посмотрим, какие значения на графике примет функция при представлении в виде кривой.

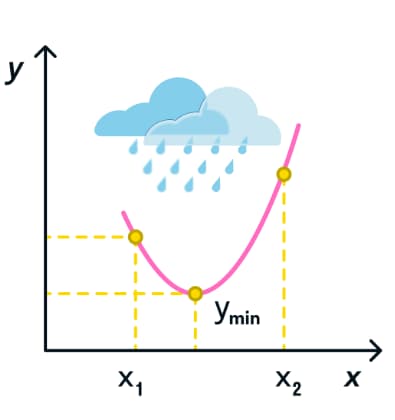
Наибольшее значение функция примет, когда кривая будет изображена в виде пика. Наименьшие значения — это низкие точки относительно пика кривой. На скрине четко отображены наибольшие и наименьшие значения этой функции.

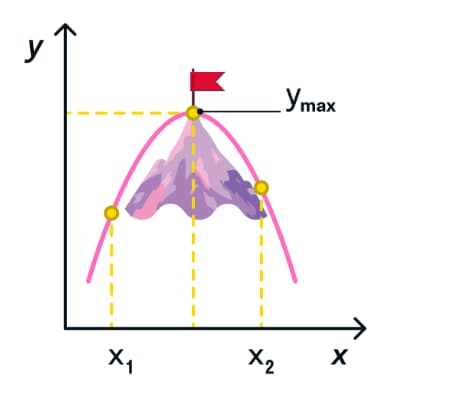
А теперь давайте посмотрим на наименьшее значение функции. Обычно так изображается дно оврага. То есть наименьшее значение функции на графике будет выглядеть как дно фужера. В то время, как максимальные значения этой функции будут по обе стороны кривой, краями фужера.

Определение наибольшего или наименьшего значения через производную

Предыдущие поиски наибольшего и наименьшего значения функции были простыми и понятными для любого старшеклассника. Однако для поиска этих же значений через производную, нужно вспомнить теорему Ферма и найти стационарные точки.

По теореме Ферма стационарные точки определяют экстремум функции. А на словах определение максимальных и минимальных значений через производную звучит так:

• отношение приращения функции к приращению аргумента при бесконечно малом приращении аргумента называется производной функции.

Производная функции показывает, как быстро увеличивается функция Y при малом увеличении X. Чтобы найти производную нам понадобится формула из следующей таблицы:

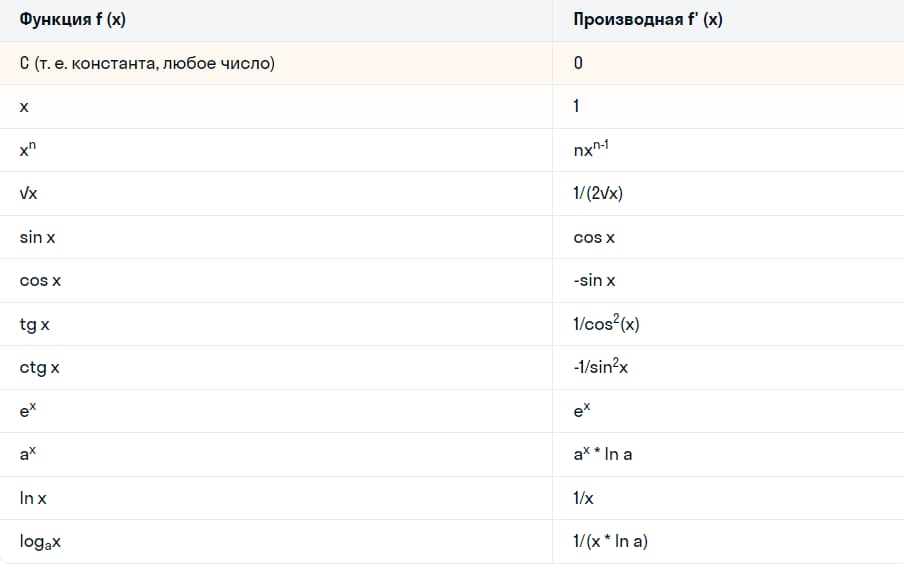
Процедура нахождения производной из функции называется дифференцированием. Например, Аня занялась гимнастикой и решила стоять на планке по 10 секунд ежедневно в течение недели. На графике это можно отобразить следующим образом:

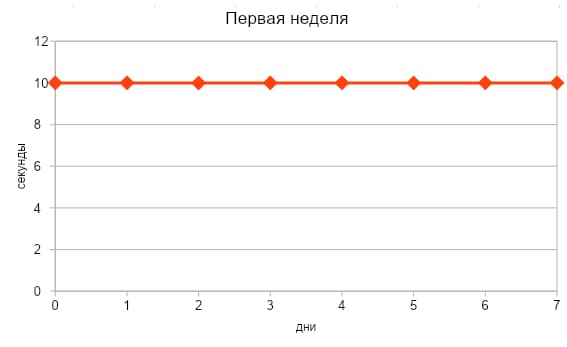
Со второй недели она начала увеличивать время стояния на 3 секунды ежедневно.

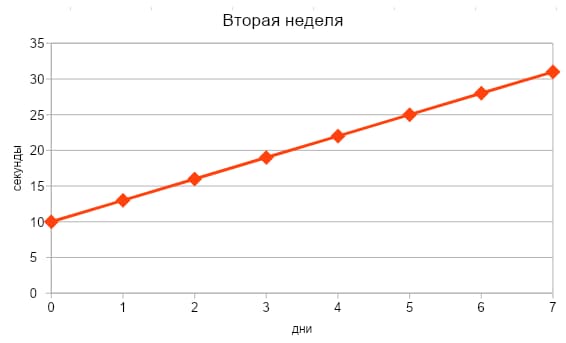
Мы знаем, что в первую неделю результаты Ани были константой. То есть скорость прироста оставалась нулевой. Давайте посмотрим в таблицу производных простых функций. В ней мы увидим, что производная константы равна нулю.

у = 10

у′ = 0

Во вторую неделю время выполнения занятий с 10 секунд начали увеличиваться на 3 сек каждый день. В итоге мы имеем формулу.

у = 10 + 3х

Чтобы найти ответ, снова необходимо заглянуть в таблицу дифференцирования производных. В ней мы найдем, что производная от х равна 1, а также по правилам вычисления производных получим следующее уравнение:

• (c*f(x))'=cf'(x) и (f(x)+g(x))'=f'(x)+g'(x);
• у = 10 + 3х;
• у′ = 0 + 3;
• у′ = 3.

Таким образом мы узнаем, что успехи Ани росли со скоростью 3 секунды в день и вычислим производную от функции.

Алгоритм нахождения на отрезке

А теперь давайте попробуем определить наименьшее и наибольшее значение функции на отрезке. У такого уравнения есть определенный алгоритм решения. Он состоит из следующих шагов:

1. В первую очередь необходимо найти область определения рассматриваемой функции и проверить, входит ли в неё указанный отрезок.
2. Для этого необходимо найти производную этой функции.
3. Затем нужно приравнять производную к нулю. То есть решим уравнение, которое покажет точки, где функция на графике обращается в 0.
4. Из полученного корня уравнения, нужно взять те точки, которые попадают в заданный промежуток, и вычислить значение функции в них.
5. После этого необходимо отметить точки начала и конца отрезка.
6. Затем необходимо найти значение функции в этих точках.
7. Таким образом мы получим результат, который расскажет нам о наибольшем и наименьшем значении функции.

Давайте посмотрим на один из примеров на скрине:

В этом примере задействован алгоритм, приведенный нами выше в статье. По нему можно находить любые наименьшие и наибольшие точки на отрезке функции.

Задачи для самопроверки

Теперь вы изучили, что такое функция и как находить наибольшее и наименьшее ее значение. Попробуйте решить примеры самостоятельно. А потом сравните с правильным решением. При прочтении задания не смотрите на решение примера.

1. Найдите наибольшее и наименьшее значения функции f (x) = 2x3 – 9x2 + 12x – 2 на отрезке [0; 3].

Как решить: Действуем в соответствии с алгоритмом.

1) D(f) = (-∞; +∞);

2) f (x) = 6x2 – 18x + 12;

3) Стационарные точки: х = 1; х = 2.

4) f(0) = -2;

• f(3) = 7;
• f(1) = 3;
• f(2) = 2;

5) fнаим.=f(0) = -2;

fнаиб.=f(3) = 7.

Ответ: Наименьшее значение функции = -2.

А наибольшее значение функции = 7.

2. Найдите два числа со знаком «+», сумма которых равна 16, а произведение наибольшее.

Как решить:

• Пусть первое число равно х, x больше 0;
• Тогда второе число будет равно формуле: (16 - х), 16 - х больше 0;
• Следовательно, х больше, чем 0, но меньше, чем 16;
• Произведение этих чисел равно х(16 – х).

Напишем функцию, как на скрине:

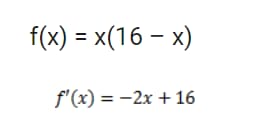
x = 8 – единственная стационарная точка на интервале (0; 16), она является точкой максимума.

Это значит, что в этой точке функция F(x) = x(16 – x) имеет наибольшее значение.

Отсюда мы имеем, что два положительных числа, сумма которых равна 16, а произведение наибольшее, это 8 и 8.

Ответ: 8 и 8

Как видите, через функции проще решать некоторые задачи и быстрее находить правильный результат.

FAQ

Как найти наибольшее и наименьшее значение функции непрерывной на интервале?

При решении этой задачи, будет действовать следующая теорема: функция y = f( x) непрерывна на промежутке Х. Внутри этого промежутка она имеет стационарную точку х0. В этом случае будут действовать следующие формулы, которые отображены на скрине:

На графиках можно отобразить эту теорему следующим образом:

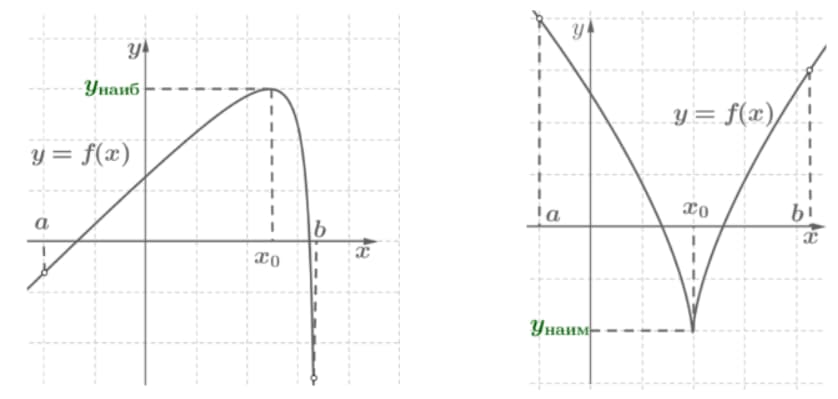
Когда называют функцию монотонной?

Если функция возрастает или убывает на интервале, то её называют строго монотонной на данном интервале.

Как понять, что такое точки экстремума и сами экстремумы?

Помните одно правило, которое распространяется на все функции. Точки экстремума – это «иксовые» значения. Экстремумы – «игрековые» значения. Будьте аккуратны в словах. Иначе экзаменаторы могут не понять вас.

Зачем нужна производная?

С помощью производной можно не только исследовать функцию, но и найти два ее значения — максимальное и минимальное. Задачи на нахождение производных точно встретятся на экзамене по профильной математике

Вывод

Теперь вы знаете, что такое функция и как находить наименьшее и наибольшее значение функции. Изучите еще раз эту статью, выучите основные правила и запомните формулы. Они помогут вам на экзамене быстро ответить на все вопросы, которые вы получите в билетах, если попадется задание на тему функций.