Модуль числа, калькулятор модуля
Модуль числа показывает расстояние между точками на числовой прямой. Кроме того, это числовая операция, используемая при решении задач не только по математике, но и по физике. Поэтому важно разобраться с этой темой и научиться применять знания на практике.
Онлайн калькуляторы – обзор сервисов
В интернете представлен большой выбор различных онлайн калькуляторов, в которых достаточно ввести исходные значения и система автоматически рассчитает ответ. Самыми популярными онлайн калькуляторами модулей, можно назвать следующие ресурсы:
- Matematika-club.ru – калькулятор может использоваться для нахождения модуля (абсолютной величины) числа или целых выражений;
- Skysmart - простой и понятный в использовании калькулятор;
- Planetcalc – ресурс может использоваться для выполнения арифметических действий по заданному модулю.
Что такое модуль числа
Объяснение для 6 класса гласит, что модулем является расстояние от определенной точки до точки координатной прямой, которая соответствует заданному числу. К примеру, если у нас есть число «а», которое изображается точкой А на координатной прямой, то расстояние от нее до нуля или начала отсчета – это отрезок ОА, который и является модулем заданного числа «а».
|а|=ОА.
Рассмотрим пример:
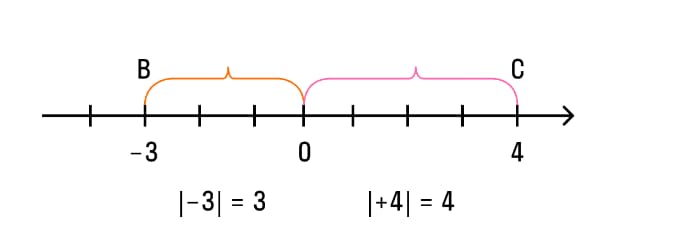
Точка В (-3) расположена от точки 0 на расстоянии 3 единиц. Поэтому длина отрезка 0В равняется 3 единицам. Длина этого отрезка или число 3 и будет модулем числа -3.
|-3|=3 или «модуль минус трех равен трем».
Точка С (+4) расположена на расстоянии 4 единиц от начала отсчета. Следовательно, длина этого отрезка равна 4 единицам. Отсюда число 4 будет модулем числа +4. |+4|=4. Плюс в данном случае допускается упустить - |4|=4.
Свойства модуля числа
Модуль имеет свои свойства:
- Модуль числа является расстояние, а оно не бывает отрицательным. Поэтому модуль всегда положительное число.
|а|>0
- Модуль положительного числа равняется этому самому числу.
|а|=а, при а>0
- Модуль отрицательного числа равен этому же числу с противоположным знаком.
|-а|=а
- Модуль нуля равняется нулю.
|0|=0, при а=0
- У противоположных чисел одинаковый модуль.
|а|=|-а|=а
- Модуль произведений равняется произведению модуля этих же чисел.
|аb|=a*b, если a*b>0
или
-(a*b), если a*b<0.
- У частного числа модуль равен частному, полученному в результате деления модуля числа числителя на модуль числа знаменателя.
|a/b|=|a|/|b|
Геометрическая интерпретация модуля
Исходя из того, что модулем числа называют расстояние от этого числа на числовой прямой до нуля. Следовательно, расстояние от -5 до 0 равно 5. Изобразим это на числовой прямой.
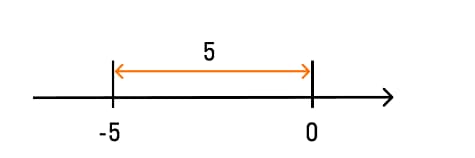
Рассмотрим геометрическую интерпретацию модуля на конкретных примерах.
|х|=5.
На числовой прямой есть 2 точки, которые удалены от нуля на 5 единиц. Это 5 и -5. Поэтому у данного уравнения есть 2 ответа: х=5 и х=-5.
Если нам даны 2 числа а и b, их разность будет равняться |а-b| или длине отрезка АВ на числовой прямой.
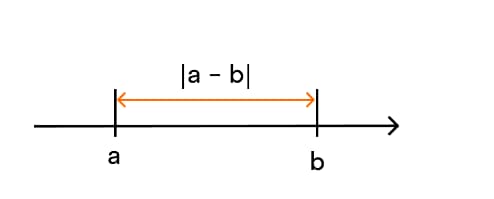
Расстояние между ними равно |а-b|=| b-а|.
Решим еще одно уравнение: |а-3|=4. Графически это выглядит следующим образом:
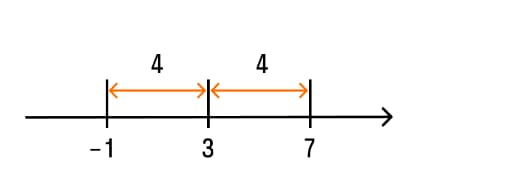
Здесь есть 2 решения -1 и 7.
Решим неравенство: |а+7|<4. Графически это выглядит следующим образом:
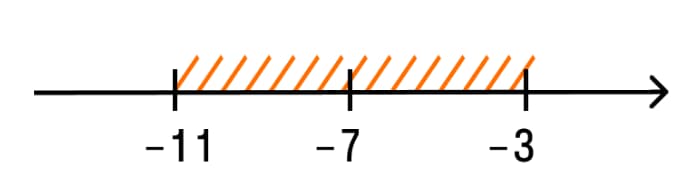
Ответ (-11; -3).
Решим неравенство: |10-х|≥ 7. Графически это выглядит следующим образом:
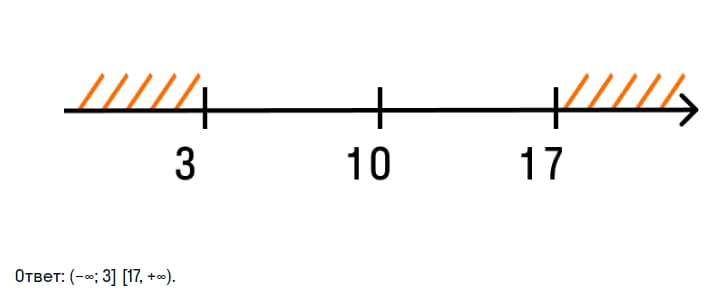
График функции
График функции равен у=|х|.
Если х>0, то у=х.
Если х<0, то у=-х.
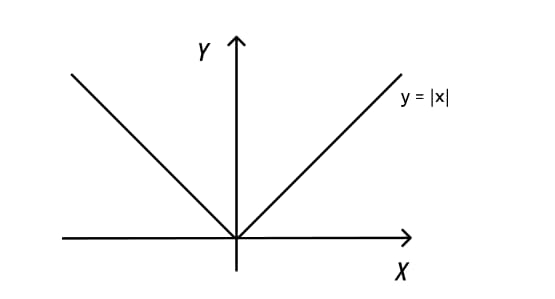
График используют для решения различных уравнений или неравенств.
Корень из квадрата
Выпускники школ при сдаче ЕГЭ могут столкнуться с заданием, где необходимо вычислить значение 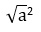 . При этом
. При этом 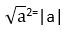 .
.
Арифметическим квадратным корнем 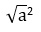 может быть неотрицательное число, у которого квадрат равняется а2. При а>0, его значение а, при а<0, его значение –а.
может быть неотрицательное число, у которого квадрат равняется а2. При а>0, его значение а, при а<0, его значение –а.
Модуль рационального числа
Модулем рационального числа называют расстояние, которое начинается в точке отсчета и идет до точки на координатной прямой, которая соответствует данному значению.
|-5,6|=5,6
|7,1|=7,1.
FAQ
Почему модуль числа изучают именно в 6 классе?
В 6 классе школьники изучают отрицательные и противоположные числа, также появляется понятие множества целых чисел. Именно поэтому в программу алгебры 6 класса введена тема модуля.
Как подготовиться к контрольной работе по теме «Модуль числа»?
Для начала школьник должен запомнить, что такое модуль. Важно понимать переход к кусочной функции, знать свойства и график модуля. Также необходимо потренироваться в практической части темы, решив задания с рабочей тетради, задачника или другого источника.
Что собой представляет график модуля?
График модуля – «галочка», расположенная выше оси х. Модуль способен зеркально отражать график любой функции х так, что у всегда оказывается больше 0.
Вывод
Модулем числа называют расстояние из начала отсчета до точки на координатной прямой с соответствующим значением. Поэтому его значение всегда будет положительным числом. Данная тема не сложная, но при решении заданий на ЕГЭ, школьники нередко допускают досадные ошибки. Чтобы этого избежать, рекомендуется внимательно отнестись к изучению модулей и закрепить свои знания на практике.
