Метод интервалов, решение неравенств

Из курса алгебры 9 класса, школьникам известно, что метод интервалов – самый простой и эффективный способ решения неравенств. Особенно этот способ подойдет при необходимости решить квадратное неравенство, у которого всего одна переменная. Расскажем, как это сделать.

Квадратное неравенство – определение

Неравенством в алгебре называют выражение с применением знаков  <, >, ≤, ≥.

Числовым неравенством является неравенство, где с двух сторон от знака записаны числа или числовые выражения. Решением неравенства является переменная, подставив которую, наше неравенство будет верным. Что значит решить неравенство? Решить его – рассчитать множество, при которых оно будет выполняться.

Квадратное неравенство имеет следующий вид:

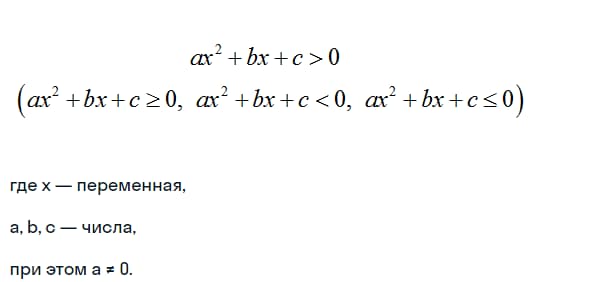
Для решения квадратного неравенства могут использоваться 2 метода:

• графический;
• метод интервалов.

Рассмотрим каждый из них более подробно.

Решение неравенства графическим методом

Чтобы решить любое квадратное неравенство, необходимо определить корни уравнения ах²+вх+с=0. Для нахождения корней, следует найти его дискриминант. Каким образом он способен повлиять на корни рассматриваемого уравнения:

1. Дискриминант равен 0 (D=0). В таком случае квадратное уравнение будет иметь только 1 корень.
2. Дискриминант больше нуля (D>0). В таком случае квадратное уравнение будет иметь 2 корня.
3. Дискриминант меньше нуля (D<0). В таком случае у квадратного уравнения вообще не будет корней.

Функция у= ах²+вх+с=0 может иметь один из представленных графиков.

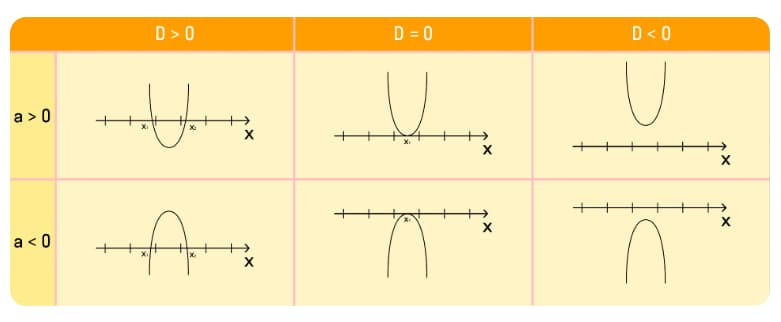
Если по условию требуется найти такой числовой промежуток, где трехчлен ах²+вх+с имеет значение больше 0, то нужно запомнить, что он будет располагаться выше оси ОХ. И наоборот, если требуется найти числовой промежуток, в котором ах²+вх+с будет меньше 0, то он будет располагаться там, где парабола ниже оси ОХ.

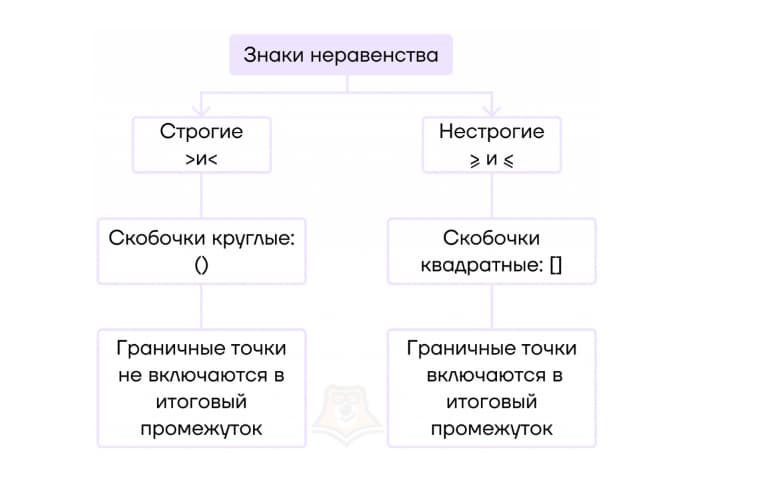
У строгого квадратного неравенства корни не будут входить в числовой промежуток, у нестрогого, они наоборот будут туда входить.

Метод интервалов для решения неравенства

Методом интервалов является особый алгоритм, используемый для удобства решения рациональных неравенств. Из уроков алгебры вспоминаем, что рациональное неравенство выглядит как f(x)≤0. f(x)здесь является рациональной функцией. Знак при этом может быть абсолютно любым.

Интервалом называют промежуток на числовой прямой, куда входят все возможные числа, ограниченные пределами (концами интервала). Их сложно представить, поэтому обычно их рисуют для лучшей визуализации.

Как решить неравенство, используя метод интервалов:

1. Первое, что нужно сделать – это найти нули трехчлена ах²+вх+с.
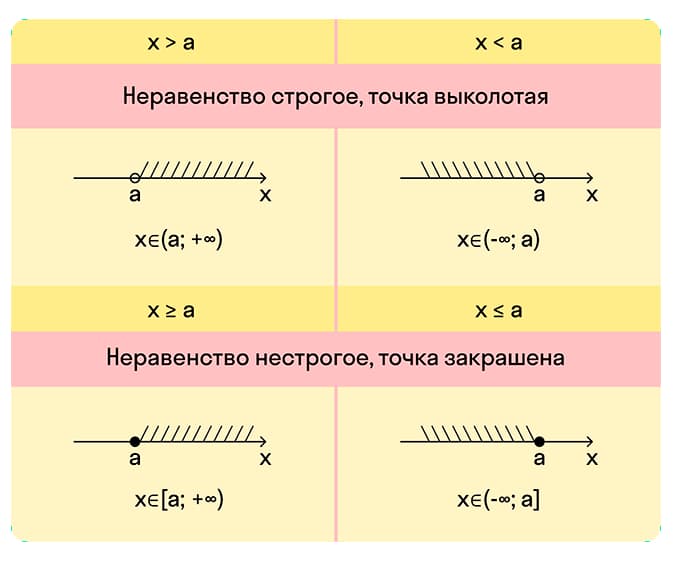
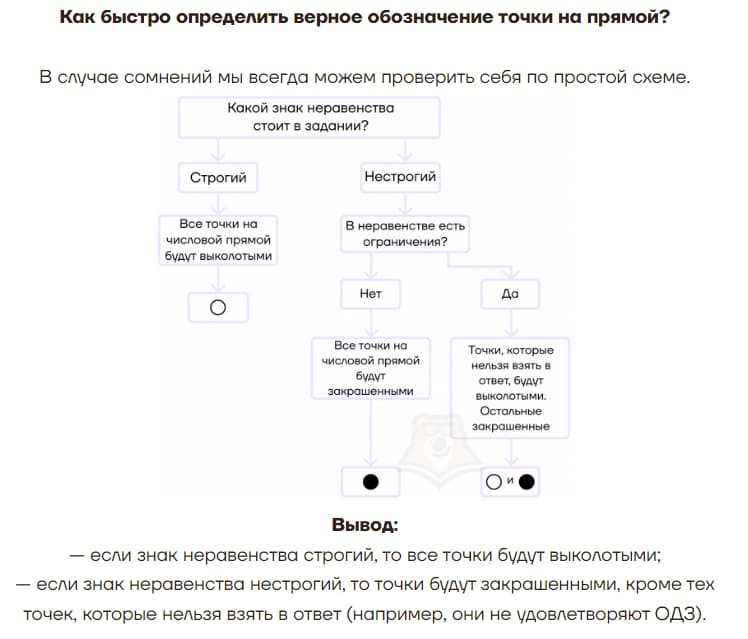
2. Отметить их на координатной прямой.
   
   
   
   При решении строгого неравенства, точки делают пустыми. В нестрогом неравенстве они будут обычными. После их нанесения, координатная прямая будет разделена на определенные промежутки.
   
   
   
   
   
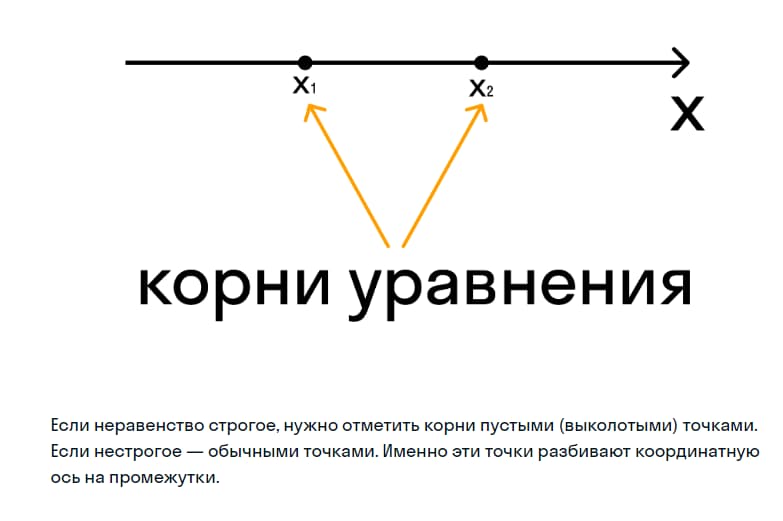
3. На следующем этапе определяются знаки трехчлена отдельно для каждого промежутка (в том случае, когда нули были найдены) или полностью на всей прямой (если нули найти не получилось). Над каждым промежутком ставится соответствующий знак + или -.
4. Если полученное квадратное неравенство имело знаки > или ≥, то на каждый плюсовой промежуток будет нанесена штриховка. Если оно имело знаки < или ≤, заштриховываются отрицательные промежутки. Штриховку можно заменить интервальными «арками». Так у нас получается геометрическое изображение числового множества.
   
   
   
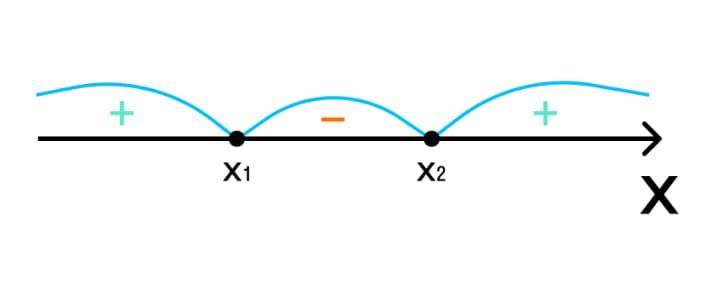
5. Последним шагом становится выбор интервалов и запись ответа.

Подробнее рассмотрим, как определить знак промежутка. Для этого найдем корни трехчлена х²+4Х-5.  Они будут равны 1 и -5. Поэтому числовая ось будет разделена на такие промежутки (-∞, -5), (-5, 1), (1, +∞).

На промежутке (1, +∞) для определения знака необходимо найти значение трехчлена, если х входит в этот промежуток. Его значение может быть любым, максимально удобным для проведения вычислений. К примеру, пусть это будет 2.

2²+4*2-5=4+8-5=7

Так как у нас получилось положительное число, то на этом интервале значение рассматриваемого трехчлена будет положительным.

Найдем знак на промежутке (-5, 1). К примеру, возьмем х=0. Отсюда:

0²+4*0-5=0+0-5=-5.

В итоге у нас получилось отрицательное значение. Поэтому здесь любое значение трехчлена окажется отрицательным.

Находим знак последнего интервала промежутки (-∞, -5). К примеру, возьмем х=-6. Отсюда:

(-6²)+4*(-6)=36-24-5=7.

В итоге у нас получилось положительное значение. Поэтому здесь любое значение трехчлена окажется положительным.

Разберем примеры – задачи и решения

FAQ

Какие бывают знаки равенства?

Они могут быть строгими или нестрогими.

Какой знак бывает в методе интервалов?

Он может быть < и ≤ или  > и ≥.

Выводы

Решение неравенств методом интервалов признан самым простым и эффективным. Он представляет собой алгоритм, освоив который можно будет легко решить неравенство.