Логарифмы

Тема логарифмов традиционно считается одной из самых сложных в математике. Логичным следствием чего становится многочисленные проблемы, возникающие у школьников и даже студентов в процессе ее изучения. Рассмотрим более детально, что представляет собой логарифм, каковые его свойства и виды, а также примеры применения на практике.

Что такое логарифм?

Древнегреческое слово «логарифм» означает «число отношений». Применительно к математике термин был сформулирована очень давно – в начале 17 века. В настоящее время под логарифмом понимается показатель степени, в которую требуется возвести основание для того, чтобы получить на выходе заданное число. Важным дополнительными условиями становятся еще два обязательных требования:

1. Значение основания превышает нуль и не равняется единице.
2. Итоговое или заданное число больше нуля.

Для большей простоты можно дать определение логарифма как перевернутой степени. Например, последняя может иметь вид: 2³= 8, где

• основанием степени становится 2;
• показателем – 3;
• а результатов возведения – 8.

Существует два обратных степени выражения. Одно – это извлечение корня, когда по результату ищется основание. Второе – логарифмирование, которое выступает темой данной статьи и предусматривает поиск степени по результату и основанию. Другими словами, степень 2³ = 8 может превращаться в log₂ 8 = 3.

Логарифм может делится на целую часть, которая называется характеристикой, и дробную, носящую название мантисса. Применительно к логарифмам необходимо понимать несколько важных моментов, включая:

1. Логарифм определяется исключительно для положительного числа (так как показательная функция принимает только такие значения).
2. Важной сферой его применения становится сравнение величин, отличающихся кратно или даже на несколько порядков.
3. Принято выделить понятие «логарифмическая спираль», имеющее множество практических примеров (в соответствии с ее правилами образуются смерчи и ураганы, формируются раковины некоторых морских животных, растут рога некоторых млекопитающих и т.д.)
4. Огромное значение для решения задач с логарифмами играет правильная их запись, что объясняется частыми ошибками школьников уже на этом этапе.

Примеры с логарифмами – как решать?

В качестве наглядного ответа на вопрос, вынесенный в заголовке и непосредственно касающийся определения логарифма, достаточно привести один пример. Он записывается как log₇ 49, что означает следующее: в какую степень требуется возвести число 7 для получения результата 49. Ответ очевиден и равняется 2 (то есть второй степени). Другими словами, log₇ 49 = 2.

Виды логарифмов

Принято выделять три основных типа логарифмов, включая:

1. Натуральный. Предусматривает использование в качестве основания так называемое число е (или Эйлера), которое является иррациональным и равняется около 2,718. Натуральные логарифмы часто используются в расчетах, поэтому для них придумана специальная формат записи, имеющая вид ln х, что фактически означает log_e x.
2. Десятичный. Предполагает использование в качестве основания 10. Логарифм удобно использовать при расчетах, в которых присутствуют круглые числа. Его запись имеет следующий формат: ljg(х) или lg(х).
3. Двоичный. В этом случае основания логарифма равняется 2. Для обозначения используется запись вида lb x. Наиболее часто двоичные логарифмы используются в программировании. Что легко объяснимо, так как в основе всех алгоритмов заложен двоичный код.

Формулы и свойства логарифмов

Основное логарифмическое тождество демонстрирует приведенная ниже формула.

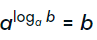
Она достаточно очевидна, что наглядно показывает пример следующего вида:

log₁₅ 15⁵ = 5.

Необходимо отметить еще несколько не менее важных свойств, изучение которых позволит лучше понять тему логарифмов и поможет грамотному применению в расчетах. В их число входят:

1. Логарифм 1 равен нулю при любом основании.
2. Логарифм, у которого основание и заданное число совпадают, всегда равняется 1.
3. Логарифм произведения двух чисел равняется сумме их логарифмов.
   
   
4. Логарифм дроби равняется разности логарифмов знаменателя и числителя, образующих ее.
   
   
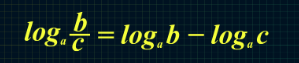
5. При возведении аргумента или основания в степень, они могут быть вынесены перед логарифмом.
   
   
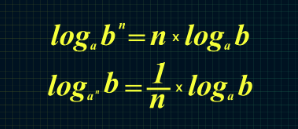
6. Основание логарифма можно заменить для удобства расчета по следующему принципу.
   
   
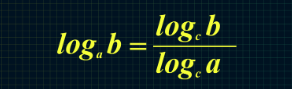
7. Следствием последней из приведенных формул становится возможность смены местами основания и аргумента, которая выполняется таким образом.
   
   

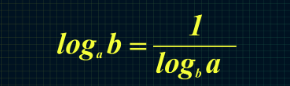
Применение логарифмических свойств в примерах

Задачи с использованием логарифмов впервые появляются в 10 или даже 11 классе. Ниже приводятся несколько достаточно простых примеров, решение которых предусматривает применение описанных выше логарифмических свойств.

Задача №1. Найти log₃ 81

Решение. 81 представляет собой 9 во второй степени. В свою очередь, 9 равняется 3 в той же степени. Поэтому исходное выражение можно преобразовать следующим образом:

log₃ 81 = log₃ 92 = _log2 3²⁺² = log₃ 3⁴.

Далее нужно воспользоваться свойством логарифма, позволяющим выносить степень. Что дает на выходе:

log₃ 3⁴ = 4 * log₃ 3 = 4 * 1 = 4.

Итоговый ответ равняется 4.

Задач №2. Найти lg 2 * lb 10

Сначала сокращенные записи двоичного и десятичного логарифма нужно преобразовать в обычные.

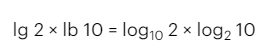
Далее необходимо оба логарифма привести к общему основанию, что позволит выполнить заданное действие и получить результат.

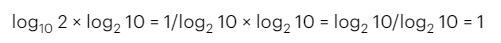
Итоговый ответ равняется 1.

Применение логарифмов на практике

Несколько примеров использования логарифмической спирали в естественной природе приведены выше. Здесь же необходимо отметить, что логарифмы широко применяются в самых разных аспектах деятельности. Начиная с теоретических наук (физика, математика, химия) и заканчивая сугубо практическими направлениями профессиональной работы (инженерия, проектирование, конструирование). Не стоит забывать о том, что знание логарифмов очень положительно влияет на итоговый балл по математике на ЕГЭ.

Онлайн-калькуляторы – обзор

Сложной рассматриваемой темы привела к появлению спроса на специализированные программы, способные производить расчет логарифмов автоматически. Сегодня найти подобный сервис не составляет труда. Причем подавляющее большинство онлайн-калькуляторов не требуют регистрации и доступны бесплатно. В качестве примера достаточно привести несколько популярных сервисов, к числу которых относятся:

• https://ru.symbolab.com/solver/logarithms-calculator;
• https://hellocalc.com/ru/log-calculator;
• https://matematika-club.ru/log.

FAQ

Что понимается под логарифмом?

Это показатель степени, возведение в которую позволяет получить из основания заданное число. Фактически логарифм является перевернутой степенью, когда требуется найти показатель степени по основанию и итоговому числу.

Какие виды логарифмов бывают?

Наиболее часто используются три типа логарифмов: натуральные, десятичные и двоичные.

Как рассчитать логарифм?

Для расчета логарифмов используются их свойства, грамотное применение которых нередко позволяет произвести необходимые вычисления вручную, то есть без специальных вспомогательных инструментов.

Можно ли использовать для вычисления алгоритмов онлайн-калькуляторы?

Да, сегодня несложно найти самые разные специализированные программы и сервисы, обеспечивающие быстрое и точное решение задачи. Большая их часть доступны бесплатно и не требуют даже регистрации.

Где на практике применяются алгоритмы?

Так называемая логарифмическая спираль (формируется на основе логарифма) достаточно часто встречается в естественной природе. В практической деятельности человека логарифмы применяются для выполнения разнообразных расчетов.

Вывод

1. Логарифм представляет собой показатель степени, в которую нужно возвести основание для получения заданного числа.
2. Бывают несколько типов логарифмов, самыми распространенными из которых выступают: натуральные, двоичные, десятичные.
3. Вычисление логарифмов базируется на нескольких свойствах, знание которых упрощает и ускоряет выполнение расчетов.
4. Логарифмы широко применяются как в теоретических исследованиях точных наук, так и в практической деятельности человека. Важным плюсом знания темы становится улучшение итоговой оценки на ЕГЭ.