Квадратичная функция – построение параболы

Квадратичная функция является одной из основных и наиболее распространенных функций в математике. Знание квадратичной функции и умение строить ее графики позволяет решать множество задач, связанных с определением экстремумов функций, нахождением корней уравнений, оптимизацией процессов и прогнозированием различных явлений и состояний.

Мы расскажем, что такое квадратичная функция, как построить квадратичную функцию и параболу, как найти вершину параболы.

Основные понятия

Для начала определим основные понятия:

Функция – это математическая связь между элементами пространства, которая позволяет определить определенные зависимости и закономерности. Другими словами, это зависимость переменной y от переменной x, при которой каждому значению x соответствует единственное значение y.

Квадратичная функция – это функция, которую можно записать формулой вида y = ax² + bx + c, где x – независимая переменная, a, b и c – это коэффициенты, задающие конкретный вид функции, причем a≠0.

Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения.

График функции – это визуальное представление зависимости между входными и выходными значениями функции. Другими словами, это кривая, которая соответствует заданной функции.

Парабола – график функции y = ax² + bx + c. Ветвями параболы называют направления построения кривой.

Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.

Построение квадратичной функции

График квадратичной функции представляет собой параболу. Чтобы схематично представить график конкретной функции нужно знать направление ветвей параболы и знак дискриминанта.

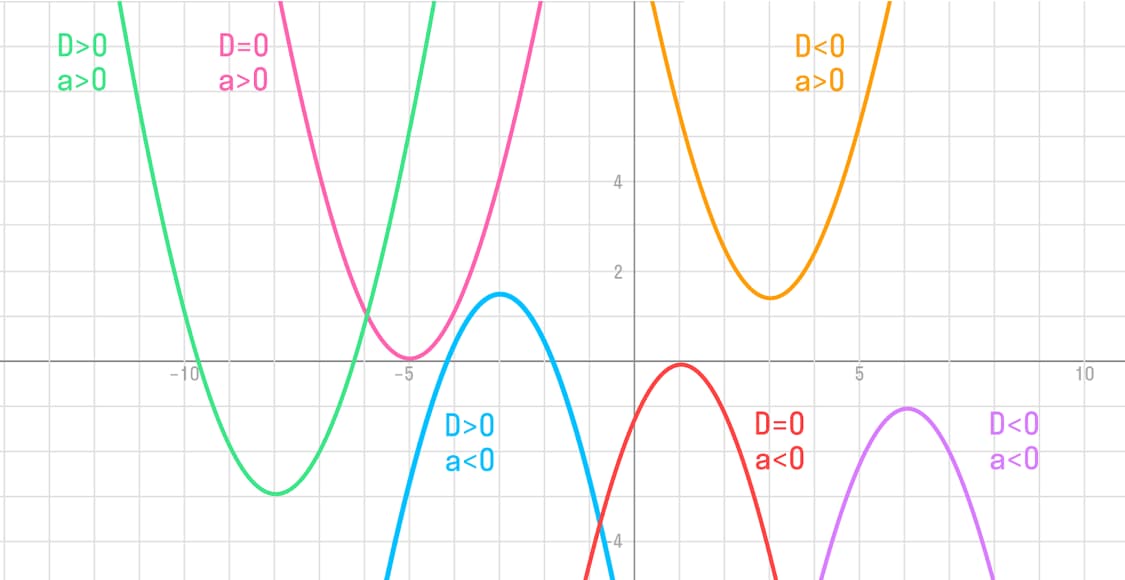
Парабола может быть направленной вверх или вниз в зависимости от знака коэффициента a:

• Когда a > 0, парабола направлена вверх и имеет вершину в точке, координаты которой определяются формулами x = -b/2a и y = f(-b/2a). В этом случае ветви параболы направлены вверх, и она имеет минимальное значение функции в вершине.
  
  
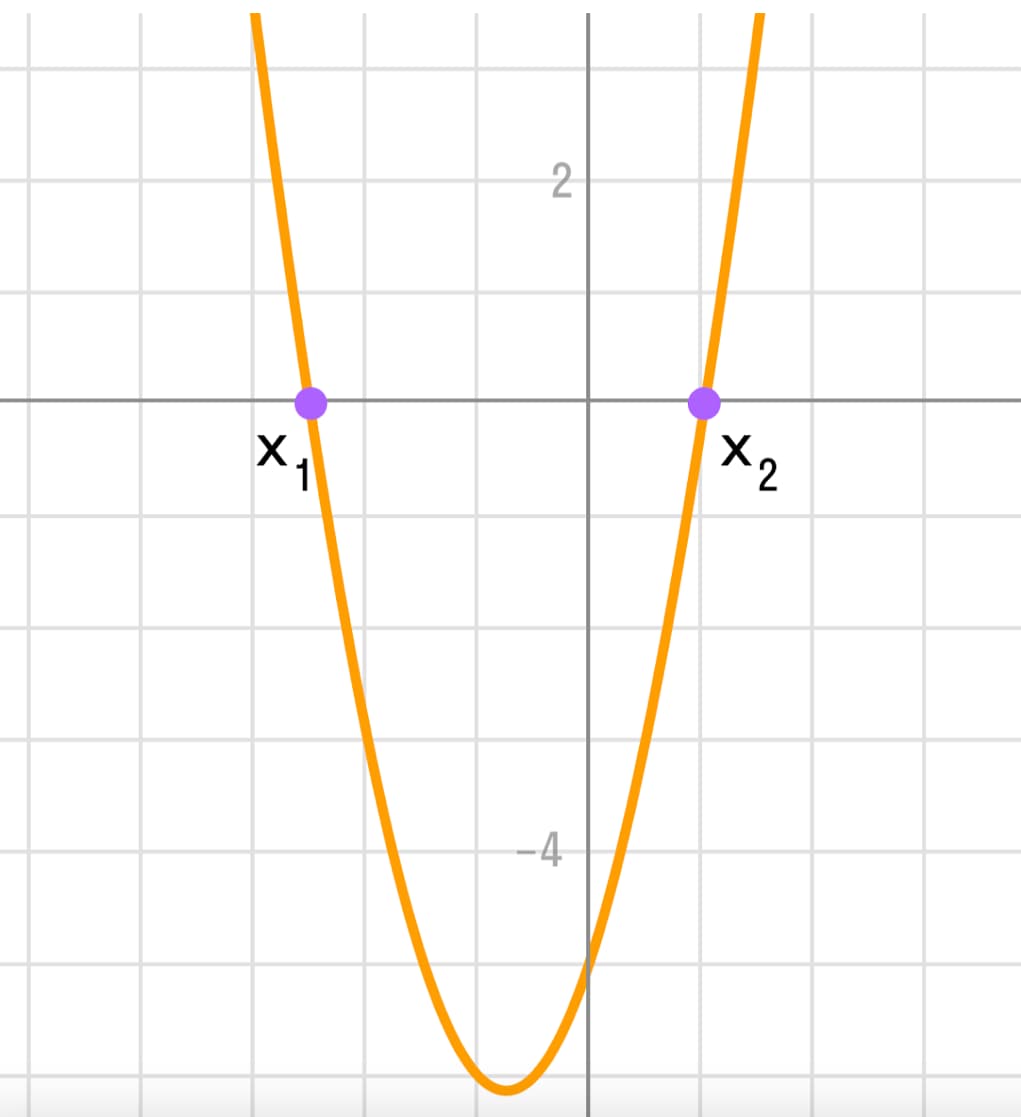
• Если же a < 0, то парабола направлена вниз и имеет вершину в точке с аналогичными координатами. В этом случае парабола открывается вниз и имеет максимальное значение функции в вершине.
• Парабола может также пересекать ось ординат в точке пересечения с осью ординат, которые определяются приравниванием функции к нулю и решением получившегося квадратного уравнения.

Для определения количества корней уравнения нужно найти дискриминант:

• При D < 0, уравнение не имеет решений, и парабола не имеет точек пересечения с осью ОХ.
• При D = 0, уравнение имеет одно решение, и парабола пересекает ось ОХ в одной точке.
• Если D > 0, то уравнение имеет два решения, а парабола пересекает ось ОХ в двух точках.

Построение параболы

Порядок построения параболы для функции y=ax²+bx+c:

• Свободный член c – это точка пересечения параболы с осью OY.
• Если а > 0:
  
  
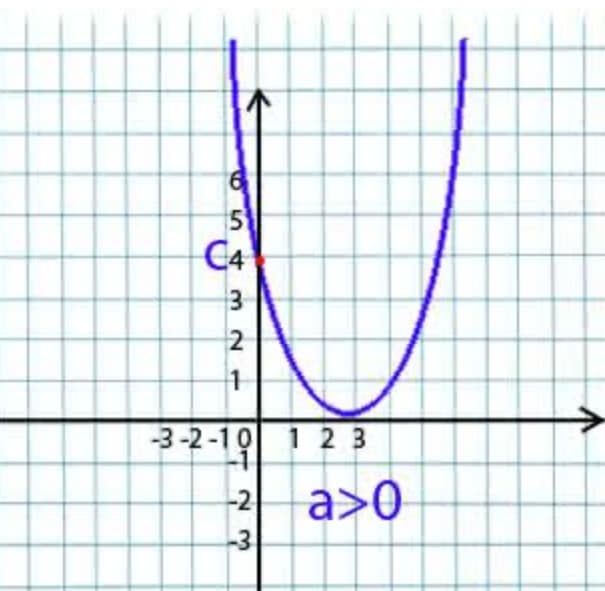
• Для определения вершины параболы применяют формулу: x=(-b)/2a.
• Нужно найти x.
• Подставляем полученное значение в уравнение параболы и находим y=-D/4а= y(х).
• Корнями уравнения называются точки пересечения параболы с осью OX. Чтобы их найти нужно приравнять уравнение к 0: ax2+bx+c=0 и решить его.

Пример:

• Задана функция: y=x2+4x+3, a=1 b=4 c=3.
• c=3 значит парабола пересекает OY в точке х=0 у=3.
• а > 0, т. е. ветви параболы направлены вверх.
• Чтобы найти вершину параболы решим уравнение: x=(-b)/2a=(-4)/(2*1)=-2
  y= (-2)2+4*(-2)+3=4-8+3=-1, т. е. вершина находится в точке (-2;-1).
• Найдем корни уравнения x2+4x+3=0.
• D=b2-4ac=16-12=4
• x=(-b±√(D))/2a
• x1=(-4+2)/2=-1
• x2=(-4-2)/2=-3
• Для построения графика отметим несколько произвольных точек, которые находятся рядом с вершиной х=-2: х = -4, -3, -1, 0.
• Подставим вместо х в уравнение y=x2+4x+3 значения:
  y=(-4)2+4*(-4)+3=16-16+3=3
  y=(-3)2+4*(-3)+3=9-12+3=0
  y=(-1)2+4*(-1)+3=1-4+3=0
  y=(0)2+4*(0)+3=0-0+3=3
• Таким образом, у = 3, 0, 0, 3.
• Можно переходить к графику квадратичной функции.

FAQ

Как задать функцию?

Есть несколько способов задания функции:

• Аналитический ( по формулам). Дает возможность посчитать функцию при произвольном значении аргумента из области определения.
• Табличный. С его помощью можно определить конкретные значения без дополнительных измерений или вычислений.
• Графический. Поможет наглядно увидеть функцию.
• Словесный.

Как решать квадратные уравнения?

Порядок решения квадратных уравнений зависит от их вида:

• Полное квадратное уравнение ax2+bx+c=0 решается через дискриминант.
• Неполное квадратное уравнение ax2+bx=0 решается путем выноса за скобки х и приравнивая частей уравнения к 0: х(ax+b)=0, х=0 и ax+b=0.
• Неполное квадратное уравнение ax2+c=0 решается переносом неизвестных перенести в одну сторону, а известных в другую. x =±√(c/a).

Вывод

• Построение параболы для квадратичной функции является важнейшим инструментом анализа и исследования функций.
• Понимание графика квадратичной функции помогает визуализировать зависимость между переменными и освоить принципы работы квадратичных функций.