Коллинеарность векторов

Что такое коллинеарность векторов

Коллинеарность векторов означает, что они лежат на одной прямой или параллельны друг другу. Векторы коллинеарны, если они либо сонаправлены, либо противоположно направлены.

Формально, два вектора 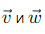 коллинеарны, если существует число k, называемое коэффициентом пропорциональности, такое что: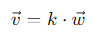

где k может быть любым числом, включая положительные, отрицательные и нулевые значения.

Важно отметить, что если два вектора коллинеарны, это не обязательно означает, что они имеют одинаковую длину. Они могут иметь различные длины, но при этом сохранять одно направление.

Признаки

Признаки коллинеарности векторов зависят от контекста, в котором они рассматриваются. Вот несколько основных признаков, которые могут указывать на коллинеарность векторов:

• Пропорциональность:
  • Два вектора коллинеарны, если они пропорциональны друг другу. Это означает, что один вектор является масштабированным вариантом другого, т.е. можно получить один вектор, умножив другой на какое-то число.
• Одно направление или противоположные направления:
  • Коллинеарные векторы могут иметь одинаковое направление или быть противоположно направленными. Если два вектора направлены в одном и том же направлении или в противоположном направлении, они коллинеарны.
• Лежание на одной прямой:
  • Два вектора коллинеарны, если они лежат на одной прямой. Это означает, что если начало одного вектора совпадает с концом другого вектора (или наоборот), то они коллинеарны.
• Линейная зависимость:
  • Векторы коллинеарны, если они линейно зависимы. То есть если существуют такие коэффициенты, при которых их линейная комбинация равна нулевому вектору.

Примеры задачи

Доказательство коллинеарности:

• Даны три вектора
• v, w и u. Нужно доказать, что они коллинеарны, используя определение коллинеарности векторов.

Поиск коэффициента пропорциональности:

• Даны два коллинеарных вектора v и w
• Нужно найти коэффициент k, такой что v =k⋅w.

Нахождение коллинеарного вектора:

• Дан вектор v
• и коэффициент пропорциональности k. Нужно найти коллинеарный вектор w , такой что v =k⋅w.

Расположение точек на прямой:

• Даны координаты нескольких точек в пространстве. Нужно определить, лежат ли они на одной прямой, используя коллинеарность векторов между этими точками.

Проверка линейной независимости:

• Даны несколько векторов. Нужно определить, являются ли они линейно независимыми или коллинеарными.