Как вычислить объем параллелепипеда

Все окружающее нас пространство состоит из параллелепипедов, объем которых полезно уметь считать не только на уроках математики, но и в быту. Например, они могут быть применены в архитектуре при проектировании зданий или в промышленности в качестве основы для различных конструкций.

В нашей статье мы расскажем, как вычислить объем обычного и прямоугольного параллелепипеда, как найти его площадь и поможем решить несколько тематических задач.

Объем параллелепипеда – что это

Параллелепипед – это геометрическое тело с 6 гранями, каждая из которых является прямоугольником. Грани этого фигурного объекта соответствуют парам параллельных прямых, и поэтому он получил такое название.

Объем параллелепипеда можно определить как произведение трех его сторон – длины, ширины и высоты. Это основная характеристика, которая позволяет определить, сколько пространства занимает данный геометрический объект.

Определение объема параллелепипеда – это один из основных элементов геометрии, который широко используется в нашей повседневной жизни. Знание объема параллелепипеда имеет практическое применение в различных сферах. Например, в строительстве, проектировании мебели или упаковочной индустрии. Зная объем помещения или объекта, можно определить необходимое количество материалов или предметов, которые могут в него вместиться.

Рассмотрим основные формулы вычисления объема параллелепипеда.

По трем сторонам

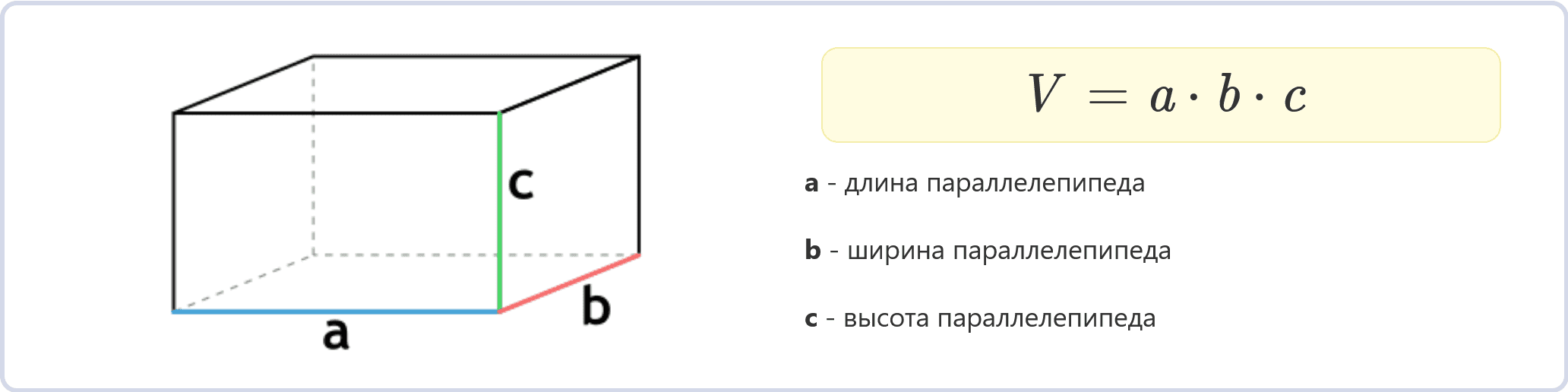
Для расчета объема параллелепипеда необходимо знать значения всех его сторон. Главная формула:

V = a * b * c, где V – объем параллелепипеда, a, b, c – длины его сторон.

Через площадь основания параллелепипеда и его высоту

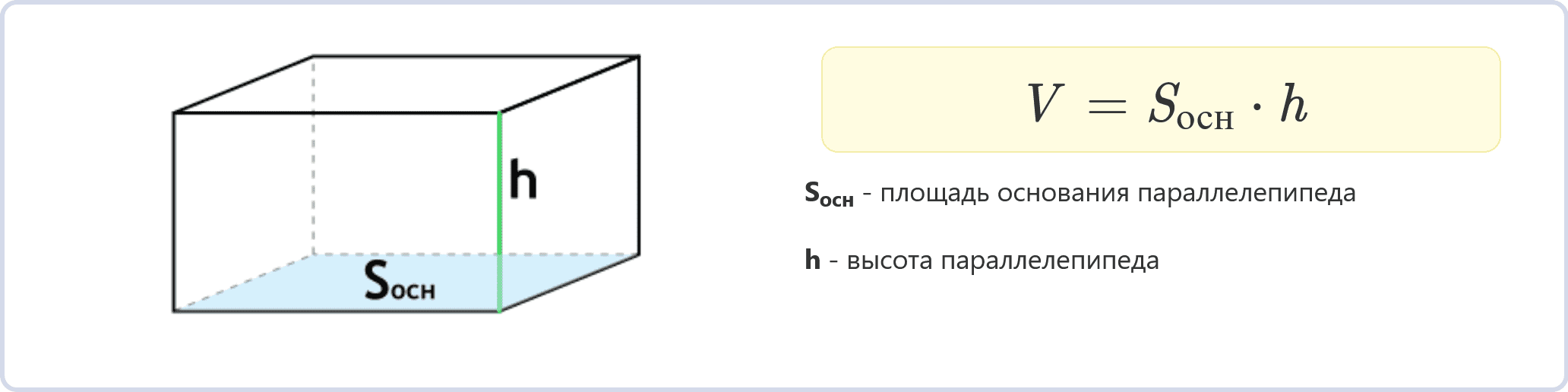
В расчете объема необходима следующая формула:

V = S_осн * h, где V – объем параллелепипеда, S_осн – площадь его основания, h – высота.

Объем прямоугольного параллелепипеда

Объем прямоугольных параллелепипедов – это объем пространства, занимаемого этим геометрическим телом. Для нахождения объема необходимо знать его длину (a), ширину (b) и высоту (c).

Формула для расчета объема прямоугольного параллелепипеда выглядит следующим образом:

V = a * b * c, где V – объем, а, b и с – соответствующие стороны параллелепипеда.

Как вычислить площадь параллелепипеда

Параллелепипед представляет собой трехмерную фигуру, имеющую шесть граней: три параллельные пары прямоугольников. Площадь вычисляется для его поверхности.

Площадь параллелепипеда равна произведению всех его сторон следующим образом:

S = 2 * (a * b + b * c + a * c), где S – площадь параллелепипеда, a, b, c – длины его сторон.

Задачи на вычисление площади параллелепипеда

Рассмотрим несколько задач на вычисление площади и объема параллелепипеда.

Вычисление площади параллелепипеда

Допустим, у нас есть параллелепипед со сторонами 5, 3 и 7 см.

Подставим эти значения в формулу, для вычисления площади:

S = 2 * (a * b + b * c + a * c)

S = 2 * (5 * 3 + 3 * 7 + 5 * 7)

S = 2 * (15 + 21 + 35)

S = 2 * 71

S = 106 см²

Таким образом, площадь параллелепипеда – 106 квадратных сантиметра.

Вычисление объема параллелепипеда по трем сторонам

У нас задан параллелепипед со сторонами 4, 6 и 8 сантиметров, мы можем найти его объем путем умножения этих значений.

Подставим эти данные в формулу, чтобы рассчитать объем:

V = a * b * c

V = 4 * 6 * 8

V = 192 см³

В данном случае, объем будет равен 192 кубическим сантиметрам.

Вычисление объема параллелепипеда через площадь основания и его высоту

Допустим, нам дано: площадь основания S_осн = 18 см², высота h = 9 см.

Подставим данные в формулу для вычисления объема:

V = S_осн * h

V = 18 * 9

V = 162 см³

Получается, что площадь геометрической фигуры составит 162 сантиметра в кубе.

Вычисление объема прямоугольного параллелепипеда

В задании даны длины трех сторон фигуры: а = 9 см., b = 13 см., c = 16 см.

Подставим данные в формулу для вычисления:

V = a * b * c

V = 9 * 13 * 16

V = 1872 см³

Таким образом, объем прямоугольного параллелепипеда будет равен 1872 см³.

FAQ

В каких единицах измеряются объем и площадь параллелепипеда?

Единицы измерения площади параллелепипеда:

• мм² (квадратный миллиметр);
• см² (квадратный сантиметр);
• дм² (квадратный дециметр);
• м² (квадратный метр);
• км² (квадратный километр).

Объем параллелепипеда измеряют в кубической единице:

• мм³ (кубический миллиметр);
• см³ (кубический сантиметр);
• дм³ (кубический дециметр);
• м³ (кубический метр).

Есть ли способы упрощения расчета объема параллелепипеда?

Да, чтобы ускорить процесс вычисления объемов, можно воспользоваться онлайн калькулятором. Вот несколько самых популярных:

• OnlineMSchool – онлайн калькулятор для вычисления объема прямоугольных и наклонных параллелепипедов. Здесь вы сможете очень просто и быстро найти объем прямоугольного параллелепипеда, зная значения его длины, ширины и высоты.
• Calc.by – онлайн калькулятор для расчета объема параллелепипеда Для работы введите значение ребер a, b, c и нажмите кнопку «Рассчитать». Также вы можете указать точность полученного результата, т.е. количество знаков после запятой, до которого будет округлен рассчитанный объем параллелепипеда.
• Ecalc – калькулятор расчета объема параллелепипеда. Здесь можно не только рассчитать площадь, но и изучить теоретическую часть, например, как вычислить диагональ прямоугольного параллелепипеда, а также посмотреть ответы на частые вопросы по теме.

Вывод

• Объем параллелепипеда – это одно из таких понятий, которое может способствовать лучшему пониманию и осознанию мира вокруг нас
• Найти объем параллелепипеда можно по нескольким формулам, которые мы подробно разобрали.
• Для тех, кто хочет упростить задачу с вычислением объема, мы нашли несколько популярных онлайн-калькуляторов.