Как умножать в столбик

Умножение чисел — основная операция в математике, которая применяется не только учениками, но и взрослыми в обычной жизни, так и в профессиональной деятельности.

Если с 3 класса знания не сохранились или возникла потребность их обновить — расскажем, как умножать столбиком, и рассмотрим примеры, чтобы запомнить этапы решения.

Умножение в столбик – основные понятия

Умножение — арифметическое действие, состоящее из 2 показателей: множитель и множимый, в результате которого получается произведение.

В математике используют 10 цифр, от 0 до 9, чтобы составить любое число.

Название каждого числа зависит от количества знаков, которое оно содержит:

• однозначное – 1 знак;
• двузначное – 2 знака;
• трехзначное – 3 знака и так далее.

Все знаки называют разрядами — место на котором стоит цифра в числе. Разряд определяют с последней цифры.

Виды разрядов:

• единиц — последняя цифра любого числа;
• десятков — предпоследняя цифра любого числа;
• сотен — перед разрядом десятков.

На место отсутствующего разряда всегда ставят 0. Например, в числе 325, на месте разряда тысяч будет ноль.

Преимущества использования метода умножения в столбик:

1. Точность. Правильное применение метода минимизирует ошибки при выполнении операции.
2. Простота. Шаги легко запомнить и просто выполнить.
3. Универсальность. Метод подходит для любых чисел без ограничений.

Умножение применяется не только в школе для выполнения контрольных и ЕГЭ. Но и в повседневной жизни. Например, сколько заплатить за 3 килограмма яблок или 2 коробки конфет и др.

Свойства умножения

Для получения верного результата необходимо знать свойства умножения и порядок их применения:

1. Переместительное свойство — от перестановки мест множителей сумма не меняется. То есть всегда действует правило a x b = b x a. Свойство применяется
   даже если в примере больше множителей.
   Например, 5 x 7 = 7 x 5 =35 или 5 x 4 x 2 = 2 x 5 x 4 = 40
2. Сочетательное свойство — произведение 3 и больше множителей не повлияет на результат, если какую-то их часть заменить произведением.
   Таким образом, действует правило a x b x c = (a x b) x c.
   Например, 2 x 3 x 4 = 2 x (3 x 4) = 2 x 12 = 24  или 2 x 3 x 4 = (2 x 3) x 4 = 6 x 4 = 24. Сочетательное свойство применяют, чтобы сократить вычисление при наличии 3 и более множителей.
3. Распределительное свойство при сложении — для умножения суммы на число нужно умножить это число на каждое слагаемое, после чего сложить полученные результаты.
   Правило свойства: (a  + b) x c = a x c + b x c. Свойство работает с любым количеством слагаемых: (a + b + c + d) x k = a x k + b x k + c x k + d x k.
4. Распределительное свойство при вычитании — при умножении разности на число нужно умножить сначала число на уменьшаемое, затем на вычитаемое и найти разницу между полученными значениями. Правило свойство в формуле: (a - b) x c = a x c - b x c.
5. Свойство нуля — если один из множителей равен нулю, произведение всегда будет 0. Для свойства верно равенство: 0 x a x b x c = 0
6. Свойство единицы — если любое число умножить на единицу. Произведение будет равно множимому. Простыми словами, чтобы не умножили на единицу, произведение будет равно числу, которое умножали:  a x 1 = a.

Алгоритм умножения в столбик

Одним из способов умножения является метод умножения в столбик, который позволяет умножать числа любой сложности.

Без деталей алгоритм умножения можно записать следующим образом:

• записал;
• умножил единицы;
• умножил десятки;
• умножил сотки.
• получил результат.

Подробно рассмотрим каждый этап на примере умножения многозначных чисел и многозначного на однозначное.

Умножение на однозначное число

Алгоритм на однозначное число состоит из 5 этапов:

1. Запишите множитель и множимое друг под другом относительно правого края.
2. Умножьте единицы нижнего числа на единицы верхнего числа и запишите результат под чертой.
3. Умножьте десятки нижнего числа на единицы верхнего числа, результат запишите под чертой, сместив на одну цифру влево.
4. Сложите полученные произведения.
5. Запишите результат в столбик под чертой.

Например, 32 х 7 = 224

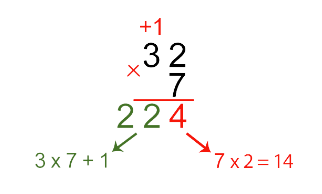
Умножение на многозначное число

Основные этапы умножения столбиком:

1. Выпишите множитель и множимое в строку как пример.
2. Определите самое маленькое число из 2, чтобы, записывая в столбик, поставить его вниз в качестве множителя.
3. Выпишите пример столбиком: вверху большое число, затем маленькое, которое ранее определили. Слева поставьте знак умножения и проведите линию, под которой запишите промежуточный и итоговый результаты.
   Важно! Выписывайте числа столбиком, чтобы разряды соответствовали друг другу: единицы должны быть под единицами и т.д.
4. Каждую цифру первого множителя умножайте на последнюю цифру второго множителя. Действие выполняйте справа налево. Если результат получился двузначным, под числом запишите только последнюю цифру, вторую перенесите в другой разряд после сложения с результатом, полученным при умножении следующего разряда.
5. При умножении второго разряда проведите действия, описанные в пункте выше. Результат записывают под чертой, сдвигая влево на 1 цифру.
6. Сложите полученные значения.

Пример:

Разберем примеры – задачи и решение

Рассмотрим пример умножения чисел 13 и 16.

Каждая цифра записывается под другой цифрой аналогичного разряда, слева поставим знак умножить.

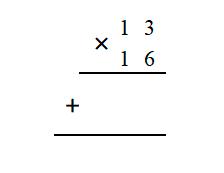
1. Верхнее число умножим на первый ряд второго числа – разряд единиц. Каждую цифру первого числа умножьте справа налево второго числа. То есть сначала получим результат произведения 13 и 6:

3 х 6 =18

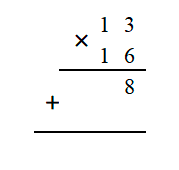
8 запишем, а единицу перенесем в следующий разряд.

2. Затем умножим 1 x 6 = 6 и добавим единицу из предыдущего действия: 6 + 1 = 7

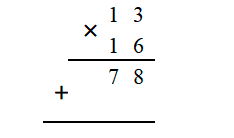
Вычислим второй промежуточный результат. Если множимое или множитель состояли бы из 3 чисел – результатов было бы 3, из четырех – 4 и т.д.

3. Умножим последовательно число 13 на вторую цифру слева, на 1. Помним свойство при умножении на 1, число множимое не изменится: 3 x 1 = 3. Запишем 3 под разрядом десятка, а вместо пустого места под цифрой 8 можно записать 0 (но не обязательно).

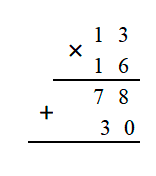
4. Затем умножим и запишем в разряд «сотен», слева от 3.

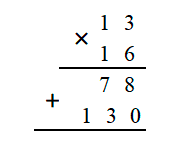
5. Сложим промежуточные результаты

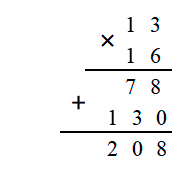
FAQ

Как избежать ошибки при умножении в столбик?

Будьте аккуратны при выполнении операций. Не забывайте смещать промежуточные результаты на разряд. Особенно если в умножении участвуют трехзначные числа и не торопитесь. Выполняйте этапы последовательно и всегда получите верный результат.

Как научится быстро умножать в столбик?

Необходимо организовать правильно сам процесс. Выписывайте результат каждого этапа. Такой лайфхак повысит эффективность решения задач и сделает результат максимально точным. Практика тоже играет ключевую роль в освоении этого метода, чем больше будете тренироваться, тем быстрее и точнее будете умножать.

Вывод

Для успешного применения методом умножения в столбик необходимо иметь понимание базовых математических операций и правильно распределить цифры по разрядам. Попробуйте применить метод умножения в столбик на практике — это отличный способ не только решать задачи более эффективно ну и насладиться процессом работы с цифрами.