Как решать систему уравнений
Посредством уравнений можно описать любые процессы. Большое количество уравнений, которым обучаются школьники в 8, 9 классе. В этих классах алгебра становится намного сложнее. Так как ученики начинают изучать уравнения, системы уравнений.
Система уравнений – что это
Уравнением называется математические равенство. В нем обычно нужно найти одну или несколько величин, которые остаются неизвестными. При чем эти величины должны иметь такие значения, при которых равенство становится верным.
Системой уравнений называется несколько уравнений. Для них нужно будет найти значения неизвестных.
Существует два типа уравнений:
- линейные с двумя переменными;
- системы двух линейных уравнений с двумя переменными.
Разберем основные понятия системы уравнений и поймем, как решать такие большие системы.
Основные понятия
Системой линейных алгебраических уравнений или СЛАУ называется объединение определенных линейных уравнений, где каждое из них содержит определенные переменные. Например, как на скрине.
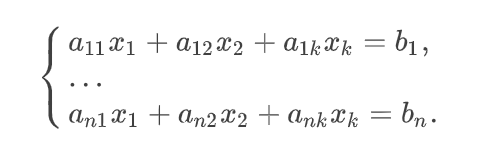
Если количество неизвестных не совпадает с количеством уравнений в системе, то эти примеры рассматриваются в старшей школе.
Чтобы решить систему уравнений, можно воспользоваться одним из двух методов. Первый способ называют методом подстановки. В народе он получил название «железобетонный» метод. Этот способ решения системы уравнений стали именовать железобетонным потому, что с помощью него всегда можно решить данные задачи.
Также есть еще один метод решения — метод сложения. С помощью этого способа вначале уравнение приводят к такому типу, в котором остается только одно неизвестное число.
Давайте рассмотрим, как решать систему уравнений по каждому из этих способов.
Как решать систему уравнений
Пример решения системы уравнений способом подстановки. Школьники изучают его с 7 класса.
- Одну переменную из первого линейного уравнения выражаем через другую переменную.
- Подставляем выраженную переменную в следующее уравнение системы.
- Получаем еще одно уравнение. Оно должно содержать только одну переменную. Далее решаем ее относительно этой переменной.
- Теперь берем значение переменной, полученное в шаге под номером 3, и подставляем в выражение для другой (первой) переменной, как в шаге № 1.
Теперь рассмотрим этот алгоритм на основе конкретного примера.
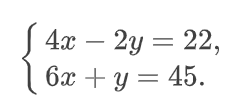
Чтобы решить СЛАУ нужно действовать согласно первого шага из описанного выше алгоритма. Выражаем одну переменную через другую. Здесь нам будет удобно из второго уравнения системы выразить переменную «y» через переменную «x». Запишем ее как на скрине.
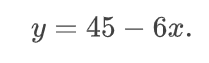
Подставляем переменную «y», выраженную через «x», в первое уравнение системы. Запишем так, как на скрине ниже.
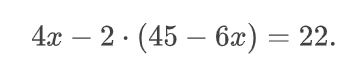
Теперь запишем новую систему уравнений, как в самом начале.
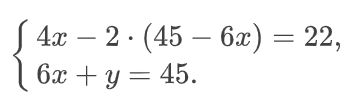
Теперь раскроем скобки и приведем уравнение к такому виду.
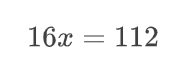
Отсюда поймем, что x = 7.
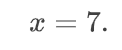
Находим число «y». Для этого подставляем значение переменной x в выражение для второй переменной.
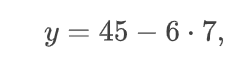
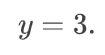
После применения этого способы к рассматриваемой системе линейных уравнений, вы увидели, что мы нашли числа 7 и 3, являющиеся решением СЛАУ.
Перейдем к следующему методу.
Линейное уравнение с 2 переменными методом сложения
Алгоритм будет следующим:
- Умножаем почленно все системы уравнения на такое число, чтобы коэффициенты при одной из переменных стали противоположными числами. Если коэффициенты при одной из переменных — противоположные значения, то сразу можно переходим к выполнению второго шага.
- Складываем правую и левую части каждого уравнения почленно. Результатом будет получение уравнения с одной переменной.
- Это уравнение решаем относительно оставшейся переменной.
- Результат найденной переменной подставляем в одно из исходных уравнений системы. Вычисляем значение второй переменной.
Вот так это будет выглядеть на «живом» примере.
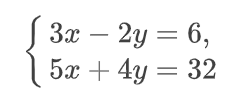
Избавляемся от переменной «y» путем почленного умножения обеих частей первого уравнения системы на 2.
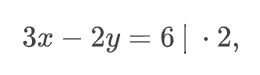
Теперь мы имеем такое уравнение.
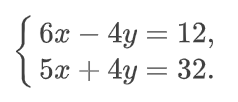
Приплюсуем к левой части первого уравнения левую часть второго уравнения. Потом тоже самое сделаем по отношению к правой части первого уравнения. Мы получаем уравнение следующего типа.
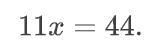
Решим это уравнение относительно единственной переменной.
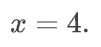
Подставляем найденное значение в первое уравнение исходной системы и ищем значение «y».
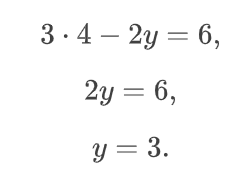
Находим числа 4 и 3. Это и есть решение системы линейных уравнений с двумя переменными.
Линейные уравнения, решаемые методом Гаусса
Способ Гаусса является обобщением метода подстановки. С помощью него можно легко находить решения систем линейных уравнений, в которых более двух уравнений и неизвестных.
FAQ
Какие еще есть методы решения СЛАУ?
Есть еще метод Крамера, решение с помощью обратной матрицы, LU разложение, разложение Холецкого (решение системы уравнений методом квадратного корня), метод прогонки (решение системы уравнений для трехдиагональной матрицы). Но к таким примерам лучше обращаться в классах старшей школы.
Можно ли школьнику 9 класса научиться решать СЛАУ онлайн с репетитором?
Да. Это вполне возможно. Ведь репетитор назначается для того, чтобы подготовить школьнике к ОГЭ и ЕГЭ.
Какие итерационные методы есть в решениях СЛАУ?
Метод простой итерации, метод Гаусса-Зейделя (еще одна модификация метода простой итерации), метод релаксации.
Вывод
Вы узнали, что такое системы уравнений, методы решения их. Обучайте школьников 7, 8 класса начиная с простейших форм уравнений и постепенно переходя на более сложные системы уравнений и методы их решения. Некоторые методы могут и не понадобиться в обычной жизни школьника, будущего студента, например, филологического факультета. Но хотя бы в общих чертах школьник обязан знать о них.
