Как решать квадратные уравнения?

Квадратные уравнения и способы их решения изучают в 8 классе общеобразовательной школы. Причем полученные знания используются до выпуска из учебного заведения. Поэтому для получения высокой оценки по алгебре и соответствующего балла ЕГЭ по математике следует уделить изучение тему самое пристальное внимание. Рассмотрим более подробно, что представляют собой квадратные уравнения, каковы способы их решения, и другие сопутствующие вопросы.

Важные определения

Квадратным уравнением принято называть уравнение, имеющее следующий вид: ax² + bx + c = 0, в котором:

• х – это неизвестная переменная, которая является корнем уравнения и которую нужно найти;
• а – старший или первый числовой коэффициент, который не должен быть равен нулю (иначе уравнение перестает быть квадратным и становится линейным);
• b – второй числовой коэффициент;
• с – свободный член уравнения.

Решение уравнения представляет собой поиск значения неизвестной (корень уравнения), при котором равенство становится верным, или доказательство отсутствия такого значения. Самым простым способом узнать, имеет ли уравнение решение, становится расчет дискриминанта (обозначается как D). Теме посвящена отдельная статья нашего сайта. Здесь же необходимо привести формулу расчета (D = b² – 4ac) и возможные варианты:

1. D>0 (что означает наличие у квадратного уравнения двух корней).
2. D=0 (один корень).
3. D<0 (корней нет).

Виды квадратных уравнений

Для лучшего понимания рассматриваемой темы нужно изучить еще два термина. Речь идет о разновидностях квадратного уравнения, которое может быть приведенным (старший коэффициент равен 1) или неприведенным (он отличается от 1). Пример первого: x² + 2х – 12 = 0. Пример второго: 8x² –х + 14 = 0.

Обязательно нужно отметить, что любое неприведенное уравнение можно преобразовать в приведенное. Для этого достаточно разделить обе части равенства на первый числовой коэффициент.

В завершении вводной темы следует выделить еще две разновидности квадратных уравнений. Первая из них – полные, в которых все три коэффициента не равняются нулю (причем a – по определению, то есть изначально). Вторая – неполные, у которых один из двух коэффициентов (b или c) равняется нулю.

Решение неполных квадратных уравнений

Знание разновидностей квадратных уравнений помогает выбрать оптимальный способ решения. Первым делом рассмотрим решение неполных квадратных уравнений. Можно выделить три их типа. Поэтому имеет смысл привести правила решения каждого.

№1. аx² = 0

В этом случае нулю равняется сразу два коэффициента – b и c. Решение уравнения не составляет труда, так как единственным корнем в этом случае становится 0. Что является прямым следствием свойств степеней.

№2. аx² + с = 0

В этом случае нулю равняется второй числовой коэффициент - b. Решение уравнения выполняется следующим образом:

1. Сначала с переносится в правую часть со сменой знака (стандартное правило переноса).
2. Далее обе части уравнения делятся на с.
3. После этого остается извлечь квадратный корень из числа, стоящего в правой части равенства.

Важно отметить, что уравнение не имеет корней, если в правой части (которая равняется с/а) стоит отрицательное число. Извлекать корень квадратный можно только при наличии положительного.

№3. аx² + bx = 0

В этом случае нулю равняется коэффициент с. Решение уравнения достигается применением метода разложения на множители. При этом выполняются следующие операции:

1. Сначала выносится за скобки х: х * (ах + b) = 0.
2. Полученное уравнение является равносильным совокупности двух, более простых: х = 0 и ах + b = 0.
3. Отсюда делается вывод о наличии двух корней: х = 0 и х = -b/а.

Решение с помощью дискриминанта

Универсальный способ решения квадратных уравнений. Предусматривает предварительное вычисление дискриминанта, что позволяет узнать количество корней (1 или 2) или их отсутствие. Далее определяется непосредственно значение переменной, для чего используется следующая формула:

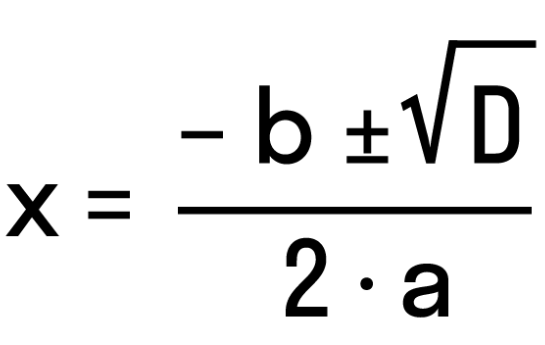
Ее следствием становится значения двух корней (если D>0), которые рассчитываются по таким формулам:

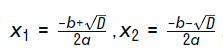
Обзор онлайн-калькуляторов для решения квадратных уравнений

Более подробно решение квадратных уравнений с помощью дискриминанта рассмотрено в другой статье нашего сайта. Здесь же необходимо отметить, что существуют и другие способы достижения аналогичного результата. Они или являются частным случаем описанных выше (например, формула корней для четного второго числового коэффициента), или достаточно сложны (формула Виета). Важным дополнением становится метод упрощения квадратных уравнений, позволяющий привести равенство в более доступный и удобный для решения вид.

Необходимо обязательно учитывать возможность решения квадратных уравнений с помощью современных онлайн-сервисов. Количество подобных интернет-ресурсов достаточно велико. В качестве примера приведем несколько простых и при этом весьма эффективных:

• https://skysmart.ru/articles/calculators/onlajn-kalkulyator-kvadratnyh-uravnenij;
• https://calc.by/math-calculators/quadratic-equations.html;
• https://ru.symbolab.com/solver/quadratic-equation-calculator;
• https://ru.onlinemschool.com/math/assistance/equation/quadratic/.

Большая часть онлайн-калькуляторов доступна в бесплатном режиме. Некоторые требуют регистрации на сайте – быстрой и удобной.

FAQ

Что понимается под квадратным уравнением?

Выражение вида ax² + bx + c = 0. Причем: а не должно равняться 0 и является вместе с b и с числовыми коэффициентами, а х – это неизвестная переменная.

Как решать квадратные уравнения?

Способ решения подбирается с учетом разновидности уравнения. Универсальный вариант решения предусматривает использование дискриминанта.

Можно ли пользоваться для решения квадратных уравнений онлайн-калькуляторами?

Да, подобные сервисы – бесплатные, удобные и точные – легко найти в интернете.

Вывод

1. Квадратным называют уравнения вида: ax² + bx + c = 0, где а, b и с – числовые коэффициенты (причем а не равно 0), а х = неизвестная переменная которую нужно найти.
2. Умение решать квадратные уравнения – обязательное условие получения высокой оценки по алгебре и аналогичного экзаменационного балла ЕГЭ по математике.
3. Универсальным способом решения квадратных уравнений выступает дискриминант.
4. Некоторые типы квадратных уравнений (например, неполные) можно решить проще и быстрее с использованием специальных способов.
5. Альтернативный вариант решения задач, содержащих квадратные уравнения, предполагает задействование онлайн-калькуляторов.