Как найти радиус окружности

Существуют задачи, для решения которых обязательно нужно знать формулы. Таким примером можно назвать задания с окружностью, где по заданным параметрам необходимо рассчитать ее площадь, длину, радиус и т. д.

Основные понятия

Проводя расчеты, необходимо понимать о чем идет речь, знать что такое радиус, окружность и круг. Для этого стоит остановиться на основных понятиях:

1. Окружность. Такое название имеет замкнутая плоская кривая, каждая из точек на ее поверхности является равноудаленной от центра, расположенного в той же плоскости. Чтобы наглядно представить себе окружность, можно вспомнить кольцо или обруч.
2. Круг – это часть плоскости, ограниченная окружностью. В качестве примера можно привести тарелку.
3. Радиус окружности. Так называется отрезок, соединяющий любую точку на поверхности окружности с ее центром.

Формула радиуса окружности

Существует несколько формул, отличающихся исходными данными и сложностью проведения расчетов.

Если известна площадь

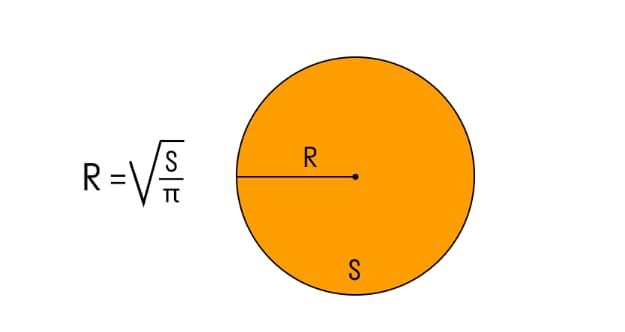
R – радиус круга;

S – площадь круга;

π – константа, равная 3,14. Она выражает отношение длины и диаметра окружности.

Если известна длина

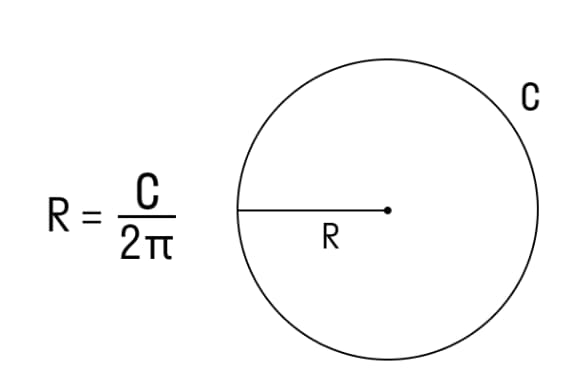
R – радиус окружности;

С – длина окружности;

π – константа, равная 3,14. Она выражает отношение длины и диаметра окружности.

Если известен диаметр

Диаметром называют отрезок, соединяющий 2 точки на поверхности окружности и проходящий через ее центр. Он всегда равен 2 радиусам.

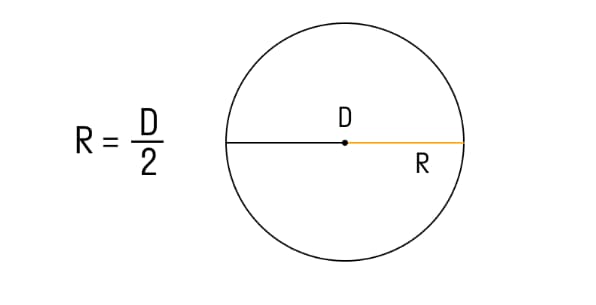
R – радиус окружности;

D – диаметр окружности.

Если известна диагональ прямоугольника, вписанного в окружность

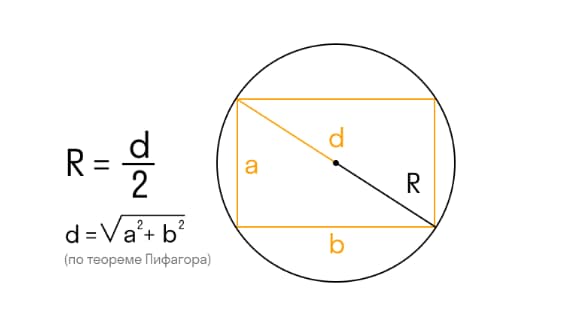
R – радиус окружности;

D – диаметр окружности;

а и b – стороны прямоугольника.

Диагональ окружности делит вписанный в нее прямоугольник на 2 прямоугольных треугольника и является их гипотенузой, то есть стороной, расположенной напротив угла в 90⁰. Вычислить диагональ можно воспользовавшись теоремой Пифагора.

Если известна сторона описанного квадрата

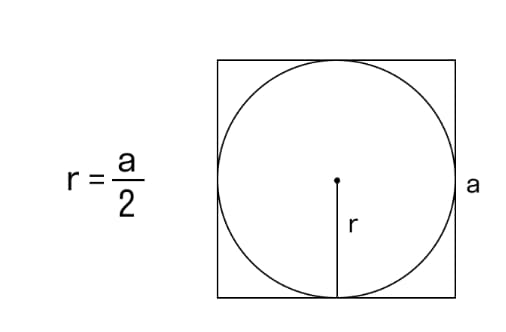
R – радиус окружности;

а – сторона квадрата.

Если известны площадь стороны вписанного треугольника

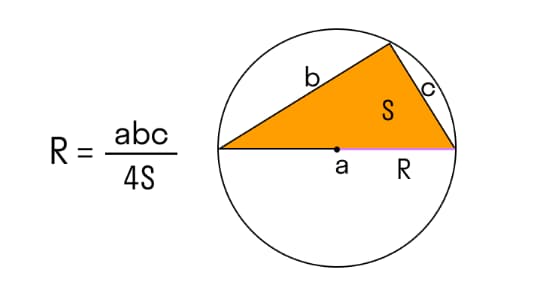
R – радиус окружности;

S – площадь треугольника;

а, b и с – стороны треугольника.

Если известны полупериметр и площадь описанного треугольника

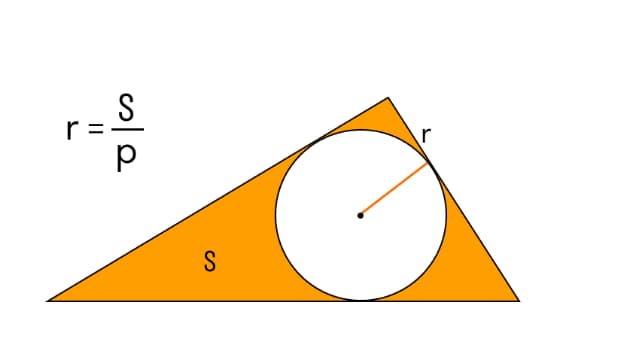
R – радиус окружности;

S – площадь треугольника;

Р- полупериметр треугольника или разделенная на 2 сумма всех его сторон.

Если известны центральный угол и площадь сектора

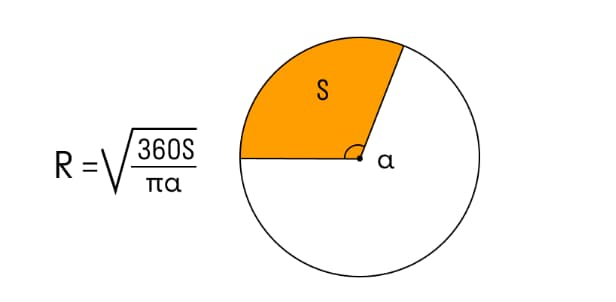
R – радиус окружности;

S – площадь сектора;

π – константа, равная 3,14. Она выражает отношение длины и диаметра окружности;

α – центральный угол.

Если известна сторона вписанного правильного многоугольника

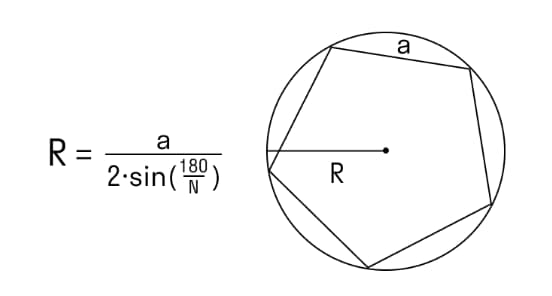
R – радиус окружности;

а – сторона многоугольника;

N – количество сторон многоугольника.

Задачи для самопроверки

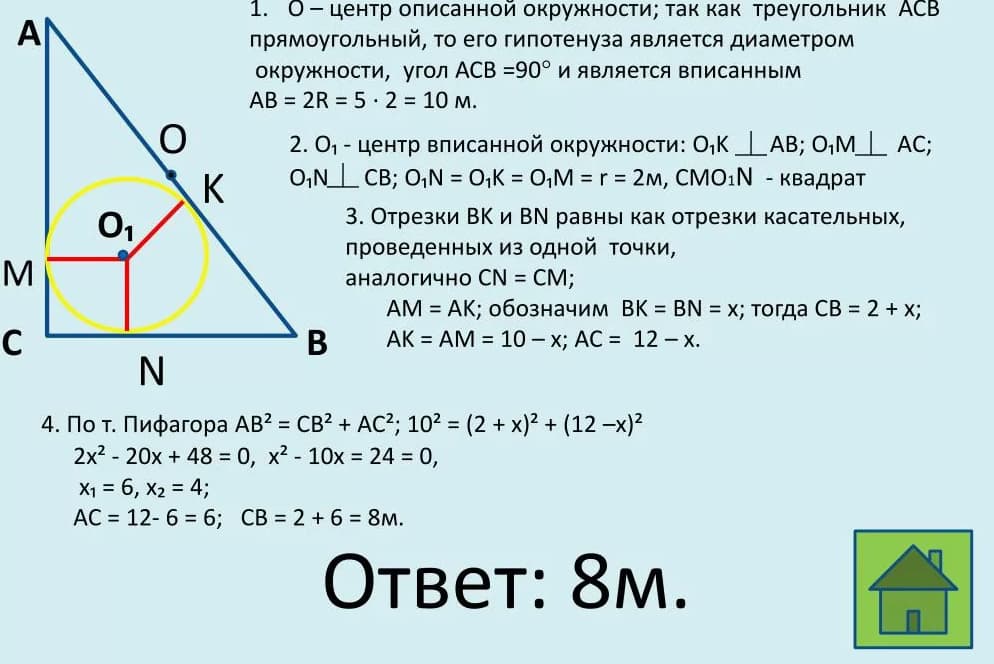
Онлайн- калькуляторы – обзор сервисов

Проверить правильность решаемых задач помогут онлайн-калькляторы:

1. Tamali.net – может рассчитать радиус любого круга или окружности.
2. Справочных портал «Калькулятор» - может рассчитать радиус круга по площади круга или длине окружности.
3. Allcalc – вводите исходные значения и получайте правильный ответ.

FAQ

В чем измеряется радиус окружности?

Это отрезок, поэтому его длина и измеряется в соответствующих величинах (мм, см, м).

Для чего нужно научиться высчитывать радиус окружности?

Это помогает выразить одну величину через другие. К целям изучения расчетов радиуса есть тренировка умений находить нужную величину, исходя из имеющихся данных (длина, площадь окружности или круга, диаметр). То есть это тренирует умения решать различные задачи.

Выводы

Рассчитывать радиус окружности не сложно. Достаточно разобраться и запомнить ряд формул. Далее подставляя в них имеющиеся данные, легко решить любую задачу.